פתרון אינפי 1, תשנ"ט, מועד ב,
(המבחן )
שאלה 1
היה בתרגול (אוהד פתר), אך לא מופיע במערכי התרגול. לכן אעתיק את הפתרון לכאן:
א) נניח ש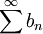 מתכנס. נפעיל את מבחן העיבוי -לכן
מתכנס. נפעיל את מבחן העיבוי -לכן 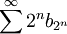 מתכנס, ולפי התנאי ההכרחי זה גורר ש
מתכנס, ולפי התנאי ההכרחי זה גורר ש 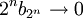 .
.
לכל n קיים k כך ש- 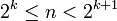 (טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת
(טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת 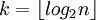 ).
).
הסדרה 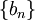 יורדת ולכן
יורדת ולכן 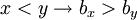 .
.
נפעיל נימוק זה על התוצאה שקיבלנו, ונקבל ש 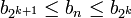 .
.
נכפיל ב (חיובי) את אגפי האי-שוויון:
(חיובי) את אגפי האי-שוויון: 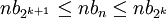
נשתמש שוב בתוצאה האלגברית: 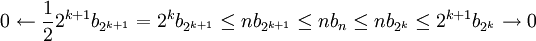
ולכן לפי משפט הסנדוויץ' נקבל את הדרוש, 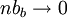 .
.
דרך נוספת:
נוכיח ש 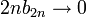 וכן
וכן 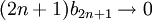 ומכאן נסיק הדרוש (כי אם תת הסדרה של האיברים במקומות הזוגיים שואפת לאפס וכן תת הסדרה של האיברים במקומות האי זוגיים שואפת לאפס אז כך גם הסדרה ).
ומכאן נסיק הדרוש (כי אם תת הסדרה של האיברים במקומות הזוגיים שואפת לאפס וכן תת הסדרה של האיברים במקומות האי זוגיים שואפת לאפס אז כך גם הסדרה ).
אם נסמן את סדרת הסכומיים החלקיים של הטור המתכנס 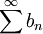 ב
ב 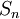 אז בגלל שהטור מתכנס מתקיים
אז בגלל שהטור מתכנס מתקיים
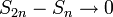 וכן
וכן
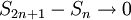 . מההתכנסות הראשונה נקבל ש
. מההתכנסות הראשונה נקבל ש 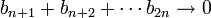 . מכיון שהסדרה מונוטונית יורדת נקבל
. מכיון שהסדרה מונוטונית יורדת נקבל 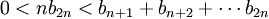 .
.
נכפיל את אי השוויונים ב2 ונשתמש משפט הסנדוויץ' כדי לקבל 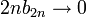 .
מההתכנסות השניה ומשיקולים דומים נקבל ש
.
מההתכנסות השניה ומשיקולים דומים נקבל ש 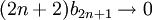 אבל
אבל
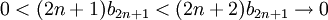 ולכן שוב ממשפט הסנדוויץ' נקבל ש
ולכן שוב ממשפט הסנדוויץ' נקבל ש 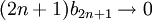 .
.
ב) דוגמה נגדית: 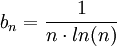 . ממבחן העיבוי הטור
. ממבחן העיבוי הטור 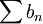 מתבדר, אך בכל זאת
מתבדר, אך בכל זאת 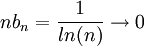 .
.
ג) ניקח את הסדרה 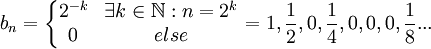 .
.
הטור 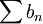 מתכנס (טור גיאומטרי עם אפסים שלא משפיעים), אבל בכל זאת
מתכנס (טור גיאומטרי עם אפסים שלא משפיעים), אבל בכל זאת 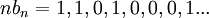 אינו מתכנס שכן יש לו תת סדרה ששווה 1 ובפרט שואפת לאחת (וידוע שאם סדרה מתכנסת לגבול אז גם כל תת סדרה שלה מתכנסת אליו).
אינו מתכנס שכן יש לו תת סדרה ששווה 1 ובפרט שואפת לאחת (וידוע שאם סדרה מתכנסת לגבול אז גם כל תת סדרה שלה מתכנסת אליו).
שאלה 2
א) נבדוק התכנסות בהחלט: ברור שהטור 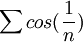 מתבדר לפי התנאי ההכרחי, שכן
מתבדר לפי התנאי ההכרחי, שכן 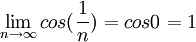 שונה מ0.
שונה מ0.
הטור מתבדר לפי התנאי ההכרחי. (כי 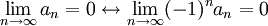 )
)
ב) נבדוק התכנסות בהחלט: 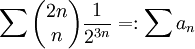 . נוכיח התכנסות בהחלט ע"י שימוש במבחן המנה:
. נוכיח התכנסות בהחלט ע"י שימוש במבחן המנה:
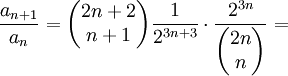
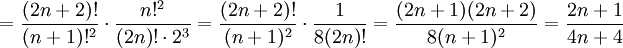
נעבור לגבול: 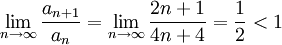 , לכן הטור מתכנס בהחלט, ובפרט מתכנס.
, לכן הטור מתכנס בהחלט, ובפרט מתכנס.
ג) מתקיים 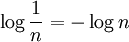 לכן הטור הוא למעשה
לכן הטור הוא למעשה
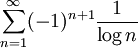 נבדוק התכנסות בהחלט:
(סימַנו כאן ln בתור לוג),
ממבחן ההשוואה נובע שהתבדרות הטור ההרמוני גוררת את התבדרות הטור
נבדוק התכנסות בהחלט:
(סימַנו כאן ln בתור לוג),
ממבחן ההשוואה נובע שהתבדרות הטור ההרמוני גוררת את התבדרות הטור
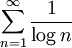 , ולכן הטור אינו מתכנס בהחלט.
הטור מתכנס בתנאי לפי משפט לייבניץ.
, ולכן הטור אינו מתכנס בהחלט.
הטור מתכנס בתנאי לפי משפט לייבניץ.
שאלה 3
א) הפונקצייה לא מוגדרת ב0, ובפרט לא רציפה שם, ובפרט לא רבמ"ש.
ב) נגזור: ![(x^{\frac{1}{3}})'=\frac{1}{3}x^{-\frac{2}{3}}=\frac{1}{3\sqrt[3]{x^2}}](/images/math/e/1/8/e18680028abef12a505aae1076c8be0c.png) .
.
בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) הפונקצייה היא רציפה בקטע סגור ולכן רבמ"ש לפי משפט קנטור.
בקרן
הפונקצייה היא רציפה בקטע סגור ולכן רבמ"ש לפי משפט קנטור.
בקרן 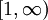 ובקרן
ובקרן ![( -\infty,-1]](/images/math/2/b/b/2bbda46f09c030f245f9afe1fa0eb85f.png) נגזרת הפונ' חסומה ולכן הפונ' רבמ"ש בכל אחת מהן.
נגזרת הפונ' חסומה ולכן הפונ' רבמ"ש בכל אחת מהן.
כעת ניזכר בכך שפונ' רציפה במ"ש באוסף סופי של קטעים שה"חיתוך" ביניהם (הגבול ביניהם... נו, אתם מבינים למה אני מתכוון) סגור (הטענה שבמערכי התרגול, עם הוכחה אינדוקטיבית עבור כל מספר סופי של קטעים, הפרכה עבור אינסופי ע"י 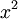 ) רציפה במ"ש גם על האיחוד הכללי שלהם, ולכן קיבלנו שהפונקצייה רציפה במ"ש בכל הישר.
) רציפה במ"ש גם על האיחוד הכללי שלהם, ולכן קיבלנו שהפונקצייה רציפה במ"ש בכל הישר.
ג)הפונ' רציפה בכל הישר כהרכבת רציפות. לפי קנטור היא רציפה במידה שווה בקטע הסגור ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) .
.
נגזור: 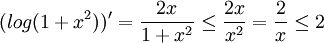 בתחום
בתחום
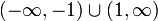 .
.
הנגזרת חסומה ולכן הפונקצייה רציפה במ"ש בקטעים ![(-\infty ,-1] and [1,\infty)](/images/math/3/5/b/35b995099055f72c64d7c023bdb5bd1d.png) .
.
הוכחנו שפונקצייה רציפה בשני קטעים מהצורה ![(a,b],[b,c)](/images/math/7/d/9/7d9d995700caea90ad4bcc21bba0900c.png) היא רציפה באיחוד שלהם.
נשתמש במשפט הנ"ל פעמיים, ונקבל שהפונ' רבמ"ש באיחוד הקטעים, שהוא
היא רציפה באיחוד שלהם.
נשתמש במשפט הנ"ל פעמיים, ונקבל שהפונ' רבמ"ש באיחוד הקטעים, שהוא 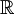 .
.
שאלה 4
4) א) הפונ' הנתונה 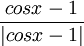 היא רציפה כהרכבת רציפות בדיוק בכל הנקודות שבהן המכנה שונה מ0, כלומר בכל
היא רציפה כהרכבת רציפות בדיוק בכל הנקודות שבהן המכנה שונה מ0, כלומר בכל 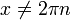 . נבדוק את סוגי האי-רציפות בנקודות שהן כן מהצורה
. נבדוק את סוגי האי-רציפות בנקודות שהן כן מהצורה 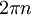 :
:
יהי 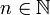 . מתקיים
. מתקיים 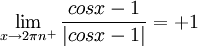 ואילו
ואילו 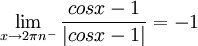 ולכן האי-רציפות היא ממין ראשון (קפיצה). בכך סיווגנו את כל נק' האי-רציפות של הפונקצייה הנתונה.
ולכן האי-רציפות היא ממין ראשון (קפיצה). בכך סיווגנו את כל נק' האי-רציפות של הפונקצייה הנתונה.
תיקון
מתקיים 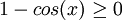
ולכן בכל מקרה בכל מקום שהפונקציה מוגדרת היא שווה ל-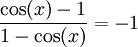 ולכן קל להראות שכל האי רציפויות סליקות
ולכן קל להראות שכל האי רציפויות סליקות
ב)הפונ' רציפה בדיוק כאשר המכנה שונה מ0, כלומר כאשר 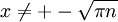 . בנקודות שהן כן מהצורה הזאת, הגבולות החד צדדיים הם שניהם 1 ולכן זאת אי רציפות סליקה.
. בנקודות שהן כן מהצורה הזאת, הגבולות החד צדדיים הם שניהם 1 ולכן זאת אי רציפות סליקה.
ג) 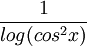 . הפונ' רציפה בדיוק כאשר פנים הלוג חיובי וגם המכנה שונה מ0, כלומר לפונ' יש אי רציפות כאשר
. הפונ' רציפה בדיוק כאשר פנים הלוג חיובי וגם המכנה שונה מ0, כלומר לפונ' יש אי רציפות כאשר 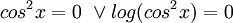 . מכאן
. מכאן 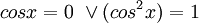 . קיבלנו ש
. קיבלנו ש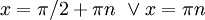 הן הנק' בהן הפונ' אינה רציפה. זה שקול ל
הן הנק' בהן הפונ' אינה רציפה. זה שקול ל 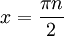 .
.
בנק' שבהן פנים הלוג אי-חיובי, כלומר שבהן הקוסינוס מתאפס, הוא חיובי משני הצדדים ולכן האי-רציפות היא סליקה.
בנק' שבהן המכנה מתאפס, הגבול משני הצדדים הוא 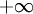 ולכן זה מין שני.
ולכן זה מין שני.
לסיכום: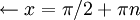 סליקה.
סליקה.
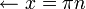 מין שני.
מין שני.
שאלה 5
5)א) אקסיומת השלמות: תהי 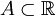 . אם
. אם 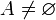 וגם
וגם  חסומה מלעיל, אזי יש ל
חסומה מלעיל, אזי יש ל חסם עליון.
חסם עליון.
ב)הלמה של קנטור - מופיעה ברשימת המשפטים. הניסוח שם:
תהי 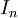 סדרה של קטעים סגורים המוכלים זה בזה
סדרה של קטעים סגורים המוכלים זה בזה 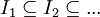 , כך שאורך הקטעים שואף לאפס. אזי קיימת נקודה יחידה c הנמצאת בכל הקטעים.
, כך שאורך הקטעים שואף לאפס. אזי קיימת נקודה יחידה c הנמצאת בכל הקטעים.
ג)משפט ערך הביניים - כנ"ל:
תהי  פונקציה הרציפה בקטע [a,b]. אזי לכל
פונקציה הרציפה בקטע [a,b]. אזי לכל 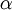 בין
בין 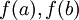 קיימת
קיימת ![c\in[a,b]](/images/math/0/0/a/00a49aece4cc72157b51ca282347a0f8.png) כך ש
כך ש 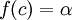 .
.
ד)כלל לופיטל:
תהיינה 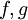 פונקציות גזירות בסביבה מנוקבת של נקודה a. אם
פונקציות גזירות בסביבה מנוקבת של נקודה a. אם 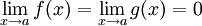 והגבול
והגבול 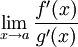 קיים, אז גם הגבול
קיים, אז גם הגבול 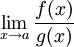 קיים, ושווה לו.
קיים, ושווה לו.
שאלה 6
6)א) סתם טכני, תשובה זוועתית. (מיותר לכתוב פתרון כשוולפראם אלפא עושה את העבודה השחורה)
ב)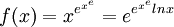 .
.
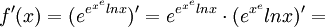
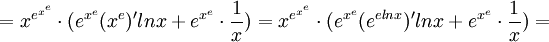
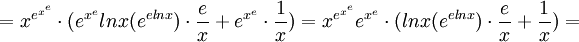
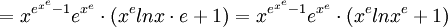
שאלה 7
7)א)הוכחנו בכיתה: תהי  פונ' גזירה ב
פונ' גזירה ב , אז הגבול
, אז הגבול 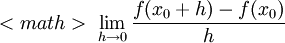 </math> קיים ושווה ל
</math> קיים ושווה ל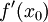 . ברור מרציפות הפונ' הלינאריות ש
. ברור מרציפות הפונ' הלינאריות ש 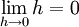 .
.
לכן: 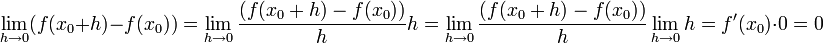
כלומר 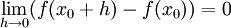 ,
,
ומכאן ש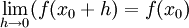 , כלומר הפונ' רציפה ב
, כלומר הפונ' רציפה ב .
.
ב) הוכחה שגוייה: הפונקצייה גזירה, ולכן הגבול שמגדיר את הנגזרת קיים. לכן קיימת סביבה נקובה ברדיוס דלתא של  שבה מרחק פונקציית הנגזרת
שבה מרחק פונקציית הנגזרת 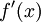 מהנגזרת
מהנגזרת 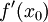 אינו עולה על אפסילון, ולכן
אינו עולה על אפסילון, ולכן 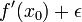 מהווה חסם מלעיל לפונקציית הנגזרת בסביבה זאת. בפרט, הנגזרת אינה חסומה.
מהווה חסם מלעיל לפונקציית הנגזרת בסביבה זאת. בפרט, הנגזרת אינה חסומה.
- הבעיה בהוכחה הנ"ל הייתה שהנחתי שהנגזרת רציפה, מה שיופרך ממש בעוד רגע. אכן, אם הנגזרת של פונקצייה היא רציפה אז המשפט נכון לפי הנימוק שהבאתי: כי מרחק פונ' הנגזרת מהגבול שלה קטן מאפסילון, והגבול שלה שווה לנגזרת ולכן סופי. (בדוגמא של נועם גבול הנגזרת בנקודה אינו סופי.)
תיקון
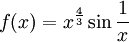 לכל
לכל 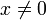 ו
ו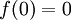 מתקיים
מתקיים 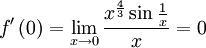 אבל מתקיים לכל
אבל מתקיים לכל 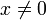 מתקיים
מתקיים 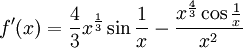 והיא כמובן לא חסומה בסביבה של 0
והיא כמובן לא חסומה בסביבה של 0
ג)הפרכנו בתרגול בקווים כלליים. (את בערך שליש מהמבחן הזה עשית איתנו, ארז...)
באופן מסודר:
נתבונן בפונ' 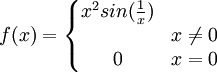 .
.
היא גזירה ב![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) , אבל הנגזרת אינה רציפה ב0.
, אבל הנגזרת אינה רציפה ב0.
נימוק: לכל 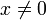 בקטע, הפונ' היא הרכבת גזירות ולכן גזירה.
בנקודה 0, עפ"י ההגדרה:
בקטע, הפונ' היא הרכבת גזירות ולכן גזירה.
בנקודה 0, עפ"י ההגדרה: 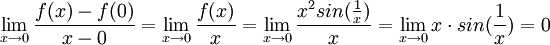 (פונ' חסומה כפול שואפת לאפס; קל לפי משפט הסנדוויץ')
(פונ' חסומה כפול שואפת לאפס; קל לפי משפט הסנדוויץ')
הגבול הנ"ל קיים ושווה 0, ולכן הוא שווה לנגזרת הפונ' בנקודה. לכן הפונקצייה אכן גזירה ב![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) .
.
הנגזרת אינה רציפה ב0, כי הגבול באפס של הנגזרת, 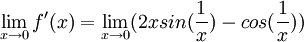 אפילו אינו קיים.
אפילו אינו קיים.
שאלה 8
8)הטענה שגוייה- הפרכנו בתרגול.