פתרון אינפי 1, תשנ"ט, מועד ב,
1) היה בתרגול (אוהד פתר), אך לא מופיע במערכי התרגול. לכן אעתיק את הפתרון לכאן:
א) נניח ש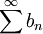 מתכנס. נפעיל את מבחן העיבוי -לכן
מתכנס. נפעיל את מבחן העיבוי -לכן 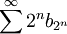 מתכנס, ולפי התנאי ההכרחי זה גורר ש
מתכנס, ולפי התנאי ההכרחי זה גורר ש 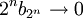 .
.
לכל n קיים k כך ש- 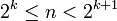 (טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת עיבוד הנוסחה נכשל (שגיאת תחביר): k=\lfloor log_2{n} \right \rfloor
).
(טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת עיבוד הנוסחה נכשל (שגיאת תחביר): k=\lfloor log_2{n} \right \rfloor
).
הסדרה 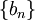 יורדת ולכן
יורדת ולכן 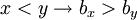 .
.
נפעיל נימוק זה על התוצאה שקיבלנו, ונקבל ש 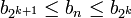 .
.
נכפיל ב (חיובי) את אגפי האי-שוויון:
(חיובי) את אגפי האי-שוויון: 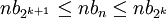
נשתמש שוב בתוצאה האלגברית: 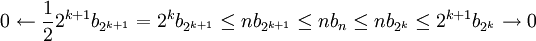 \
\
ולכן לפי משפט הסנדוויץ' נקבל את הדרוש - 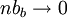 .
.
ב) דוגמה נגדית: 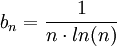 . ממבחן העיבוי הטור
. ממבחן העיבוי הטור 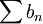 מתבדר, אך בכל זאת
מתבדר, אך בכל זאת 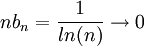 .
.
ג) ניקח את הסדרה 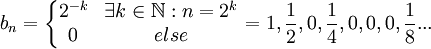 .
.
הטור 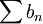 מתכנס (טור גיאומטרי עם אפסים שלא משפיעים), אבל בכל זאת
מתכנס (טור גיאומטרי עם אפסים שלא משפיעים), אבל בכל זאת 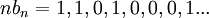 אינו מתכנס שכן יש לו תת סדרה ששווה 1 ובפרט שואפת לאחת (וידוע שאם סדרה מתכנסת לגבול אז גם כל תת סדרה שלה מתכנסת אליו).
אינו מתכנס שכן יש לו תת סדרה ששווה 1 ובפרט שואפת לאחת (וידוע שאם סדרה מתכנסת לגבול אז גם כל תת סדרה שלה מתכנסת אליו).
2)א) נבדוק התכנסות בהחלט: ברור שהטור 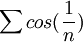 מתבדר לפי התנאי ההכרחי, שכן
מתבדר לפי התנאי ההכרחי, שכן 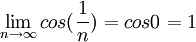 שונה מ0.
שונה מ0.
הטור מתכנס בתנאי לפי מבחן לייבניץ.
ב)