הבדלים בין גרסאות בדף "פתרון אינפי 1, תשס"ג, מועד ב,"
| שורה 11: | שורה 11: | ||
<math>\lim_{n \to \infty }{}a_n-b_n=a-b\Rightarrow \exists N_1 \in \mathbb{N}:\forall n \in \mathbb{N}: (n\geq N\rightarrow |a_n-b_n-(a-b)|<\epsilon )</math> | <math>\lim_{n \to \infty }{}a_n-b_n=a-b\Rightarrow \exists N_1 \in \mathbb{N}:\forall n \in \mathbb{N}: (n\geq N\rightarrow |a_n-b_n-(a-b)|<\epsilon )</math> | ||
| + | נגדיר: | ||
<math>N\overset{\underset{\mathrm{def}}{}}{=}max\left \{ N_1,N_2 \right \}</math>. | <math>N\overset{\underset{\mathrm{def}}{}}{=}max\left \{ N_1,N_2 \right \}</math>. | ||
| + | |||
| + | |||
| + | אז לכל <math>n \geq N</math> מתקיים <math> |a_n+b_n-(a+b)|<\epsilon \wedge |a_n-b_n-(a-b)|<\epsilon )</math>, כלומר | ||
| + | <math> |a_n-a+b_n-b|<\epsilon \wedge |a_n-a-(b_n-b)|<\epsilon </math>, | ||
| + | |||
| + | נחבר את שני האי-שוויונים: <math> |a_n-a+b_n-b|+|a_n-a-(b_n-b)|<2\epsilon </math> | ||
| + | |||
| + | אבל לפי אי-שוויון המשולש <math>2|a_n-a|=|2(a_n-a)|=|a_n-a+b_n-b+a_n-a-(b_n-b)| \leq |a_n-a+b_n-b|+|a_n-a-(b_n-b)|<2\epsilon | ||
| + | </math>. נצמצם ב2 ונקבל ש<math>\lim_{n \to \infty }{a_n}=a</math>. כעת נחסר את המשוואות במקום לחבר, ונקבל באותו האופן עבור b. | ||
| + | |||
| + | מש"ל! (התרגיל הזה והתרגיל הבא די יפים :)) | ||
| + | |||
6) הוכחה: רוצים להראות שהפונקצייה <math>f|_{R^+}</math> היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD) | 6) הוכחה: רוצים להראות שהפונקצייה <math>f|_{R^+}</math> היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD) | ||
גרסה מ־13:11, 1 בפברואר 2012
1) נכון. זאת ההגדרה.
2)נכון. נתבונן בסדרת הסכומים החלקיים: מכיוון שהטור חיובי היא עולה במובן החלש (אינדוקצייה טריוויאלית - מוסיפים איברים אי-שליליים). נתון שהיא חסומה. סדרה זאת היא חסומה ומונוטונית ולכן מתכנסת, ולכן הטור מתכנס עפ"י הגדרה.
5) הוכחה: יהי 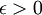 .
.
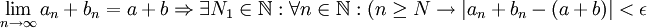
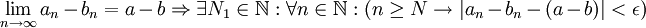
נגדיר:
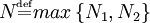 .
.
אז לכל 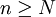 מתקיים
מתקיים 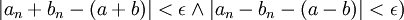 , כלומר
, כלומר
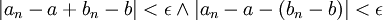 ,
,
נחבר את שני האי-שוויונים: 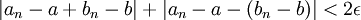
אבל לפי אי-שוויון המשולש 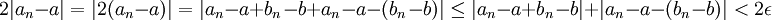 . נצמצם ב2 ונקבל ש
. נצמצם ב2 ונקבל ש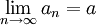 . כעת נחסר את המשוואות במקום לחבר, ונקבל באותו האופן עבור b.
. כעת נחסר את המשוואות במקום לחבר, ונקבל באותו האופן עבור b.
מש"ל! (התרגיל הזה והתרגיל הבא די יפים :))
6) הוכחה: רוצים להראות שהפונקצייה 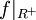 היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD)
היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD)
יהי 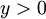 . נגדיר
. נגדיר 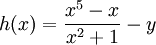 .
.
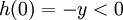 , ואילו מכיוון ש
, ואילו מכיוון ש 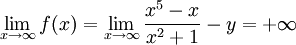 , קיימת נקודה d עבורה
, קיימת נקודה d עבורה 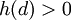 . לפי משפט ערך הביניים, יש נקודה
. לפי משפט ערך הביניים, יש נקודה  בקטע
בקטע 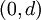 שבה
שבה 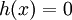 , כלומר
, כלומר 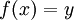 !
!
7) הפרכה: נתבונן בפונ'
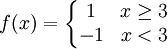 בקטע
בקטע 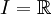 .
.
ברור ש אינה רציפה ב3, משום שהגבולות החד-צדדיים שונים, אבל
אינה רציפה ב3, משום שהגבולות החד-צדדיים שונים, אבל 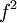 היא קבועה ולכן רציפה בכל הישר הממשי.
היא קבועה ולכן רציפה בכל הישר הממשי.