ידוע שמטריצות דומות <=> צורת ז'ורדן שלהן זהה. נראה של A,B יש צורת ז'ורדן שונה, ולכן הן אינן דומות:
נז'רדן את  :
:
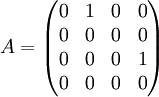
נמצא פ"א:
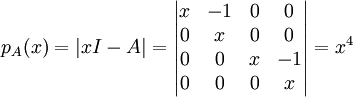
שכן דטר' של מטר' משולשית שווה למכפלת איברי האלכסון הראשי.
כעת, 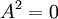 ולכן
ולכן  נילפוטנטית מסדר 2, והפ"מ שלה הוא
נילפוטנטית מסדר 2, והפ"מ שלה הוא 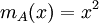 .
.
דרגת המטריצה היא 2 (מס' השורות הלא אפסיות, אחרי שמחליפים שורות והיא הופכת למטריצת מדרגות), והיא נילפוטנטית, ולכן 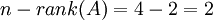 הוא מס' הבלוקים בצורת ז'ורדן. לכן צורת ז'ורדן של
הוא מס' הבלוקים בצורת ז'ורדן. לכן צורת ז'ורדן של  היא
היא
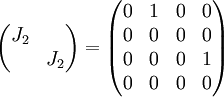 .
.
כעת נז'רדן את  :
:
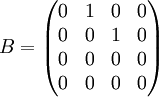
נמצא פ"א:
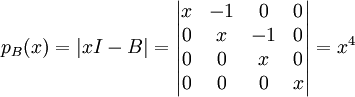
כעת נמצא את אינדקס הנילפוטנטיות של B, ובכך גם את הפ"מ שלה:
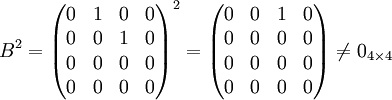
ואילו 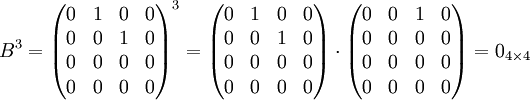
ולכן B נילפ' מאינדקס 3, והפ"מ שלה הוא 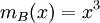 .
.
לכן בצורת ז'ורדן של  יופיע בלוק ז'ורדן נילפוטנטי מסדר 3, והמטריצה היא מסדר 4; לכן צורת ז'ורדן של A היא
יופיע בלוק ז'ורדן נילפוטנטי מסדר 3, והמטריצה היא מסדר 4; לכן צורת ז'ורדן של A היא 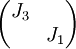 .
.
קיבלנו שצורות ז'ורדן של שתי המטריצות הנתונות שונות, ולכן הן אינן דומות.
מש"ל סעיף א'.
סעיף ב': ידוע מלינארית 1 שמתקיים 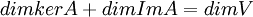 ,
כאשר
,
כאשר  המ"ו שעליו פועלת הטרנספורמציה A (
המ"ו שעליו פועלת הטרנספורמציה A (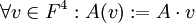 )
)
ולכן 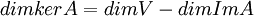 .
.
ידוע גם 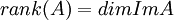 =מספר השורות הלא אפסיות בצורה המדורגת של A, כלומר 2.
=מספר השורות הלא אפסיות בצורה המדורגת של A, כלומר 2.
כמו כן 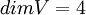 שכן מסתכלים על A כעל הע"ל מהמרחב
שכן מסתכלים על A כעל הע"ל מהמרחב 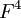 לעצמו.
לעצמו.
לכן בסה"כ 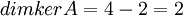 .
.
באופן דומה עבור  , מתקיים
, מתקיים 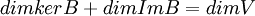 , ולכן
, ולכן 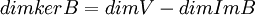 .
.
ידוע גם 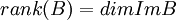 =מספר השורות הלא אפסיות בצורה המדורגת של B, כלומר 2.
=מספר השורות הלא אפסיות בצורה המדורגת של B, כלומר 2.
כמו כן 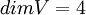 שכן מסתכלים על B כעל הע"ל מהמרחב
שכן מסתכלים על B כעל הע"ל מהמרחב 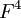 לעצמו.
לעצמו.
לכן בסה"כ 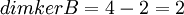 .
.
(ידוע ש-A היא המטריצה המייצגת של הטרנספורמציה המוגדרת בעזרתה וכו' - כל זה מלינארית 1, אין צורך לפרט)
לסיכום, קיבלנו 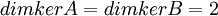 .
מש"ל!
.
מש"ל!