פתרון לינארית 2, אונ' עברית, תשס"ה, מועד א, שאלה 9
למה- יחידות צורת ז'ורדן עבור אופרטור בעל ע"ע יחיד:
ניסוח- יהי 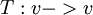 אופרטור שהפ"א שלו הוא חזקה של x-\lambda), אזי צורת ז'ורדן של T יחידה עד כדי שינוי סדר הבלוקים.
הוכחה- בשלילה, נניח של-
אופרטור שהפ"א שלו הוא חזקה של x-\lambda), אזי צורת ז'ורדן של T יחידה עד כדי שינוי סדר הבלוקים.
הוכחה- בשלילה, נניח של- יש הצגה חרת, אבל אז נקבל הצגה אחרת גם לאופרטור עיבוד הנוסחה נכשל (פונקציה \lambdaI לא מוכרת): T-\lambdaI
, שידוע שהוא נילפוטנטי, בסתירה ליחידות במשפט ז'ורדן הנילפוטנטי.
יש הצגה חרת, אבל אז נקבל הצגה אחרת גם לאופרטור עיבוד הנוסחה נכשל (פונקציה \lambdaI לא מוכרת): T-\lambdaI
, שידוע שהוא נילפוטנטי, בסתירה ליחידות במשפט ז'ורדן הנילפוטנטי.
יהי 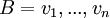 בסיס של
בסיס של 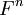 , המז'רדן את הט"ל
, המז'רדן את הט"ל 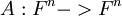 המוגדרת ע"י
המוגדרת ע"י 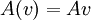 .
.
יהי  ע"ע של T. נשנה את סדר איברי B, כך שסדר הבלוקים יהיה כזה שכל הבלוקים המתאימים ל-
ע"ע של T. נשנה את סדר איברי B, כך שסדר הבלוקים יהיה כזה שכל הבלוקים המתאימים ל-  , כלומר מהצורה
, כלומר מהצורה 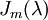 , יהיו בחלק השמאלי-עליון של הסכום הישר; בניסוח יותר מדוייק, אם נציג את צורת ז'ורדן כסכום ישר של בלוקי ז'ורדן, אז הבלוקים המתאימים ל-
, יהיו בחלק השמאלי-עליון של הסכום הישר; בניסוח יותר מדוייק, אם נציג את צורת ז'ורדן כסכום ישר של בלוקי ז'ורדן, אז הבלוקים המתאימים ל- יהיו הראשונים בסכום.
אזי
יהיו הראשונים בסכום.
אזי ![[T]_b=\begin{pmatrix}
A_\lambda & \\
& A'
\end{pmatrix}=A_\lambda\oplus A'](/images/math/7/6/c/76c1c853dbe76d8a1757dae9709d2139.png) , כאשר
, כאשר 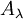 היא המטריצה האלכסונית-בלוקים של כל הבלוקים מהצורה
היא המטריצה האלכסונית-בלוקים של כל הבלוקים מהצורה 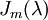 , ואילו
, ואילו 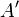 היא סכום ישר של בלוקי ז'ורדן מהצורה
היא סכום ישר של בלוקי ז'ורדן מהצורה 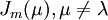 .
.
יהי k הר"א של  , אזי
, אזי 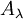 היא מסדר
היא מסדר 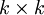 , ולכן גודלה נקבע חד-ערכית ע"י T, ולכן ע"י A (שכן T נקבעת חד-ערכית ע"י A)
, ולכן גודלה נקבע חד-ערכית ע"י T, ולכן ע"י A (שכן T נקבעת חד-ערכית ע"י A)
ידוע שמתקיים ![A_\lambda=[T]_{\left \{ v1,...,vk \right \}}](/images/math/f/6/0/f60b28f1609da61e36491642c26e7758.png) , כאשר
, כאשר 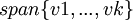 אינווריאנטי תחת
אינווריאנטי תחת  .
.
לכן, 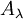 היא צורת ז'ורדן של האופרטור
היא צורת ז'ורדן של האופרטור 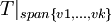 , והפ"א שלו הוא חזקה של
, והפ"א שלו הוא חזקה של 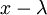 . לפי הלמה, מספר הבלוקים
. לפי הלמה, מספר הבלוקים 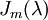 מכל גודל
מכל גודל 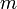 נקבע באופן יחיד ע"י
נקבע באופן יחיד ע"י  .
.