הבדלים בין גרסאות בדף "פתרון ליניארית 2, אונ' בר אילן, תשעא, מועד א', שאלה 4"

גרסה מ־23:07, 8 בינואר 2012

השאלה: נניח שלמטריצות 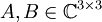$A,B\in \mathbb{C}^{3 \times 3}$ יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות $A$ ו $B$ דומות.

פתרון:

הרעיון בכלליות: נראה שעבור כל צורה של פ"א ופ"מ (בהתאם לאופייני) למטריצות A, B אותה צורת ג'ורדן ולכן הן דומות. בגלל שהסדר שלהן קטן יחסית (כי מהחל מסדר 4 המשפט לא מתקיים, אבל אותו רעיון של הוכחה יעבוד עבור סדר 2) אז יש רק צורה אפשרית אחת (עד כדי סדר בלוקים) לכל בחירה של אופייני ומינימלי.

סימונים:

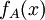$f_{A}(x)$ הפולינום האופייני של המטריצה A

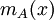$m_{A}(x)$ הפולינום המינימלי של המטריצה A

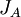$J_{A}$ צורת הג'ורדן של המטריצה A

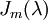$J_{m}(\lambda )$ בלוק ג'ורדן מסדר m המתאים לערך העצמי $\lambda$

אנו יודעים ש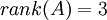 $rank(A)=3$ ולכן גם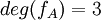 $deg(f_{A})=3$

נפצל את הפתרון לכמה מקרים:

אם ל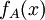 $f_{A}(x)$ שלושה שורשים שונים, כלומר שלושה ע"ע שונים.

אז לפי משפט, שתי המטריצות לכסינות ודומות למטריצה מהצורה:

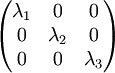
$\begin{pmatrix} \lambda _{1} & 0& 0\\ 0& \lambda _{2}&0 \\ 0&0 & \lambda _{3} \end{pmatrix}$

ולכן דומות בניהן.

אם ל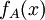 $f_{A}(x)$ שורש אחד, כלומר ע"ע אחד

אז 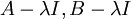$A-\lambda I, B-\lambda I$ (כאשר למדא הוא הע"ע) הן מטריצות נילפוטנטיות ובגלל שכל פולינום מעל 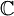$\mathbb{C}$ מתפרק לגורמים לינאריים מתקיים:

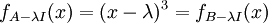
$f_{A-\lambda I}(x)=(x-\lambda)^{3}=f_{B-\lambda I}(x)$

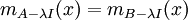
$m_{A-\lambda I}(x)=m_{B-\lambda I}(x)$

אחרת נקבל שיש שורש שונה מ- $\lambda$ לפולינום האופייני ולכן גם אין ערך עצמי יחיד.

לכן מספיק להראות שעבור כל פ"מ שנבחר יש צורת ג'ורדן אפשרית יחידה ששתי המטריצות יהיו דומות לה:

*למטה פתרון פשוט יותר

ניעזר בעובדה שהדרגה של הפ"מ, היא אינדקס הנילפוטנטיות של המטריצה, שהוא הגודל של הבלוק הגדול ביותר בצורת הג'ורדן.

אם 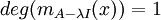$deg(m_{A-\lambda I}(x))=1$ אז גודל הבלוק הגדול ביותר הינו 1 ולכן:

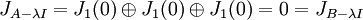
$J_{A-\lambda I}=J_{1}(0)\oplus J_{1}(0)\oplus J_{1}(0)=0=J_{B-\lambda I}$

אם 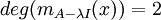$deg(m_{A-\lambda I}(x))=2$ אז גודל הבלוק הגדול ביותר הינו 2 ונותר מקום רק לבלוק ג'ורדן מגודל 1 ולכן:

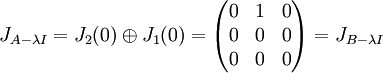
$J_{A-\lambda I}=J_{2}(0)\oplus J_{1}(0)=\begin{pmatrix} 0 & 1 & 0\\ 0& 0& 0\\ 0& 0 & 0 \end{pmatrix}=J_{B-\lambda I}$

אם 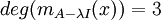$deg(m_{A-\lambda I}(x))=3$ אז גודל הבלוק הגדול ביותר הינו 3 (והוא בעצם כל צורת הג'ורדן):

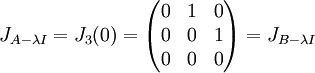
$J_{A-\lambda I}=J_{3}(0)=\begin{pmatrix} 0 & 1 & 0\\ 0& 0& 1\\ 0& 0 & 0 \end{pmatrix}=J_{B-\lambda I}$

בסה"כ הראנו שבכל מצב למטריצות 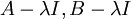$A-\lambda I, B-\lambda I$ אותה צורת ג'ורדן ולכן הן דומות.

מכאן, קיימת 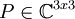$P\in \mathbb{C}^{3x3}$ הפיכה כך שמתקיים: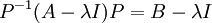 $P^{-1}(A-\lambda I)P=B-\lambda I$

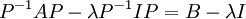
$P^{-1}AP-\lambda P^{-1}IP=B-\lambda I$

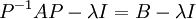
$P^{-1}AP-\lambda I=B-\lambda I$

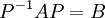$P^{-1}AP=B$ ובסה"כ הראנו שהמטריצות A וB דומות.

אם ל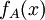 $f_{A}(x)$ שני שורשים אז בהכרח מתקיים:

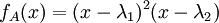
$f_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})$

וגם, 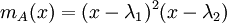$m_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})$

או 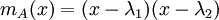$m_{A}(x)=(x-\lambda _{1})(x-\lambda _{2})$

נראה שוב, שלמטריצות אותה צורת ג'ורדן עבור שני המקרים הללו:

מקרה 1: 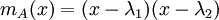$m_{A}(x)=(x-\lambda _{1})(x-\lambda _{2})$

צורת הג'ורדן של המטריצה הנ"ל הינה סכום ישר של צורות ג'ורדן של שתי המטריצות המקיימות את התנאים הבאים:

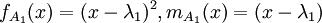
$f_{A_{1}}(x)=(x-\lambda_{1} )^{2}, m_{A_{1}}(x)=(x-\lambda_{1} )$

מטריצה כזו הינה מהצורה: 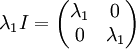$\lambda _{1} I=\begin{pmatrix} \lambda _{1} & 0\\ 0& \lambda _{1} \end{pmatrix}$

והבלוק השני מגודל 1 הינו מהצורה 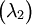$\begin{pmatrix} \lambda _{2} \end{pmatrix}$

ובסה"כ צורת הג'ורדן של המטריצה הינה: 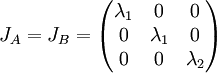$J_{A}=J_{B}=\begin{pmatrix} \lambda _{1} & 0& 0\\ 0& \lambda _{1} &0 \\ 0& 0& \lambda _{2} \end{pmatrix}$

הראנו שמדובר באותה צורת ג'ורדן ולכן המטריצות A וB דומות.

מקרה 2: 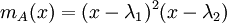$m_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})$

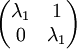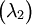
במקרה זה הבלוקים הנוצרים (באופן זהה) הינם: $\begin{pmatrix} \lambda _{1} & 1\\ 0& \lambda _{1} \\ \end{pmatrix}$ ו- $\begin{pmatrix} \lambda _{2} \end{pmatrix}$

ולכן צורת הג'ורדן של המטריצה הינה: 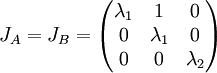$J_{A}=J_{B}=\begin{pmatrix} \lambda _{1} & 1 & 0\\ 0& \lambda _{1} & 0\\ 0& 0& \lambda _{2} \end{pmatrix}$

בסה"כ, במקרה זה לA וB אותה צורת ג'ורדן ולכן הן דומות.

לסיכום, הראנו שבכל מצב אפשרי המטריצות A וB דומות ומכאן שהן דומות.

מ.ש.ל.

פתרון פשוט יותר

(בלי להעביר לצורה נילפוטנטית)

הגדרה:

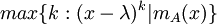
האינדקס של ערך עצמי $\lambda$ הוא $max\{k : (x-\lambda)^{k}\vert m_{A}(x)\}$

כאשר יש ע"ע יחיד הפולינום האופייני הוא 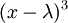$(x-\lambda)^{3}$ כמו שהראנו קודם

בגלל שהפולינום המינימלי מחלק את הפולינום האופייני האינדקס של 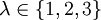$\lambda\in\{1,2,3\}$

נניח שהאינדקס 1

נקבל שהבלוק ג'ורדן הכי גדול בצורת ג'ורדן הוא מסדר 1

כלומר קיבלנו מטריצה סקלרית 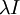$\lambda I$ ולכן היא יחידה

נניח שהאינדקס 2

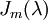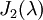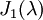
נקבל שבצורת ג'ורדן הבלוק הכי גדול $J_{m}(\lambda)$ הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ $J_{2}(\lambda)$ , $J_{1}(\lambda)$

נניח שהאינדקס 3

נקבל שיש רק בלוק אחד מסדר 3

בסופו של דבר הראנו שהפולינום האופייני והמינימלי מגדירים באופן יחיד את צורת הג'ורדן ולכן נניח יש ל-A ול-B אתו פוינום אופיינו ומינימלי נקבל:

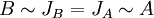
$B\sim J_{B}=J_{A}\sim A$

ומטרנזיטיביות של דמיון מטריצות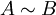 $A \sim B$

נניח שיש 2 שורשים שונים 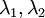$\lambda_{1},\lambda_{2}$ כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות :

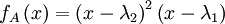
$f_{A}\left(x\right)=\left(x-\lambda_{2}\right)^{2}\left(x-\lambda_{1}\right)$

נבדוק כל אחד מהאפשרויות עבור האינדקס של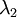 $\lambda_{2}$

נניח שהוא 1

נקבל שכל בלוק הוא מסדר 1 (כי האינדקס קטן מהריבוי האלגברי והריבוי האלגברי של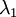 $\lambda_{1}$ הוא 1) ולכן יש צורת ג'ורדן יחידה אלכסונית

נניח שהוא 2

נקבל שקיים בלוק מסדר 2 וזה חייב להיות 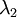$\lambda_{2}$ ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם:

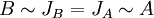
$B\sim J_{B}=J_{A}\sim A$

ומטרנזיטיביות של דמיון מטריצות $A \sim B$

@@ שורה 151: / שורה 151: @@
 '''הגדרה:'''
-האינדקס של ערך עצמי <math>\lambda</math> הוא <math>max\{k|(x-\lambda)^{k}/m_{A}(x)\}</math>
+האינדקס של ערך עצמי <math>\lambda</math> הוא <math>max\{k : (x-\lambda)^{k}\vert m_{A}(x)\}</math>
 כאשר יש ע"ע יחיד הפולינום האופייני הוא <math>(x-\lambda)^{3}</math> כמו שהראנו קודם

הבדלים בין גרסאות בדף "פתרון ליניארית 2, אונ' בר אילן, תשעא, מועד א', שאלה 4"

גרסה מ־23:07, 8 בינואר 2012

פתרון פשוט יותר

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים