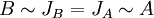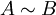|
|
| שורה 3: |
שורה 3: |
| | | | |
| | '''פתרון:''' | | '''פתרון:''' |
| − |
| |
| − | '''הרעיון בכלליות:'''
| |
| − | נראה שעבור כל צורה של פ"א ופ"מ (בהתאם לאופייני) למטריצות A, B אותה צורת ג'ורדן ולכן הן דומות. בגלל שהסדר שלהן קטן יחסית (כי מהחל מסדר 4 המשפט לא מתקיים, אבל אותו רעיון של הוכחה יעבוד עבור סדר 2) אז יש רק צורה אפשרית אחת (עד כדי סדר בלוקים) לכל בחירה של אופייני ומינימלי.
| |
| − |
| |
| − | סימונים:
| |
| − |
| |
| − | <math>f_{A}(x)</math> הפולינום האופייני של המטריצה A
| |
| − |
| |
| − | <math>m_{A}(x)</math> הפולינום המינימלי של המטריצה A
| |
| − |
| |
| − | <math>J_{A}</math> צורת הג'ורדן של המטריצה A
| |
| − |
| |
| − | <math>J_{m}(\lambda )</math> בלוק ג'ורדן מסדר m המתאים לערך העצמי <math>\lambda </math>
| |
| − |
| |
| − |
| |
| − |
| |
| − | אנו יודעים ש<math>rank(A)=3</math> ולכן גם <math>deg(f_{A})=3</math>
| |
| − |
| |
| − | נפצל את הפתרון לכמה מקרים:
| |
| − |
| |
| − |
| |
| − | '''אם ל<math>f_{A}(x)</math> שלושה שורשים שונים, כלומר שלושה ע"ע שונים.'''
| |
| − |
| |
| − | אז לפי משפט, שתי המטריצות לכסינות ודומות למטריצה מהצורה:
| |
| − |
| |
| − | <math>\begin{pmatrix}
| |
| − | \lambda _{1} & 0& 0\\
| |
| − | 0& \lambda _{2}&0 \\
| |
| − | 0&0 & \lambda _{3}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | ולכן דומות בניהן.
| |
| − |
| |
| − |
| |
| − | '''אם ל<math>f_{A}(x)</math> שורש אחד, כלומר ע"ע אחד'''
| |
| − |
| |
| − | אז <math>A-\lambda I, B-\lambda I</math> (כאשר למדא הוא הע"ע) הן מטריצות נילפוטנטיות ובגלל שכל פולינום מעל <math>\mathbb{C}</math> מתפרק לגורמים לינאריים מתקיים:
| |
| − |
| |
| − | <math>f_{A-\lambda I}(x)=(x-\lambda)^{3}=f_{B-\lambda I}(x)</math>
| |
| − |
| |
| − | <math>m_{A-\lambda I}(x)=m_{B-\lambda I}(x)</math>
| |
| − |
| |
| − | אחרת נקבל שיש שורש שונה מ-<math>\lambda</math> לפולינום האופייני ולכן גם אין ערך עצמי יחיד.
| |
| − |
| |
| − | לכן מספיק להראות שעבור כל פ"מ שנבחר יש צורת ג'ורדן אפשרית יחידה ששתי המטריצות יהיו דומות לה:
| |
| − |
| |
| − | ''*למטה פתרון פשוט יותר''
| |
| − |
| |
| − | ניעזר בעובדה שהדרגה של הפ"מ, היא אינדקס הנילפוטנטיות של המטריצה, שהוא הגודל של הבלוק הגדול ביותר בצורת הג'ורדן.
| |
| − |
| |
| − | אם <math>deg(m_{A-\lambda I}(x))=1</math> אז גודל הבלוק הגדול ביותר הינו 1 ולכן:
| |
| − |
| |
| − | <math>J_{A-\lambda I}=J_{1}(0)\oplus J_{1}(0)\oplus J_{1}(0)=0=J_{B-\lambda I}</math>
| |
| − |
| |
| − |
| |
| − | אם <math>deg(m_{A-\lambda I}(x))=2</math> אז גודל הבלוק הגדול ביותר הינו 2 ונותר מקום רק לבלוק ג'ורדן מגודל 1 ולכן:
| |
| − |
| |
| − | <math>J_{A-\lambda I}=J_{2}(0)\oplus J_{1}(0)=\begin{pmatrix}
| |
| − | 0 & 1 & 0\\
| |
| − | 0& 0& 0\\
| |
| − | 0& 0 & 0
| |
| − | \end{pmatrix}=J_{B-\lambda I}</math>
| |
| − |
| |
| − |
| |
| − | אם <math>deg(m_{A-\lambda I}(x))=3</math> אז גודל הבלוק הגדול ביותר הינו 3 (והוא בעצם כל צורת הג'ורדן):
| |
| − |
| |
| − | <math>J_{A-\lambda I}=J_{3}(0)=\begin{pmatrix}
| |
| − | 0 & 1 & 0\\
| |
| − | 0& 0& 1\\
| |
| − | 0& 0 & 0
| |
| − | \end{pmatrix}=J_{B-\lambda I}</math>
| |
| − |
| |
| − | בסה"כ הראנו שבכל מצב למטריצות <math>A-\lambda I, B-\lambda I</math> אותה צורת ג'ורדן ולכן הן דומות.
| |
| − |
| |
| − | מכאן, קיימת <math>P\in \mathbb{C}^{3x3}</math> הפיכה כך שמתקיים: <math>P^{-1}(A-\lambda I)P=B-\lambda I</math>
| |
| − |
| |
| − | <math> P^{-1}AP-\lambda P^{-1}IP=B-\lambda I</math>
| |
| − |
| |
| − | <math> P^{-1}AP-\lambda I=B-\lambda I</math>
| |
| − |
| |
| − | <math> P^{-1}AP=B</math> ובסה"כ הראנו שהמטריצות A וB דומות.
| |
| − |
| |
| − |
| |
| − | '''אם ל<math>f_{A}(x)</math> שני שורשים אז בהכרח מתקיים:'''
| |
| − |
| |
| − | <math>f_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})</math>
| |
| − |
| |
| − | וגם, <math>m_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})</math>
| |
| − |
| |
| − | או <math>m_{A}(x)=(x-\lambda _{1})(x-\lambda _{2})</math>
| |
| − |
| |
| − | נראה שוב, שלמטריצות אותה צורת ג'ורדן עבור שני המקרים הללו:
| |
| − |
| |
| − |
| |
| − | '''מקרה 1:''' <math>m_{A}(x)=(x-\lambda _{1})(x-\lambda _{2})</math>
| |
| − |
| |
| − | צורת הג'ורדן של המטריצה הנ"ל הינה סכום ישר של צורות ג'ורדן של שתי המטריצות המקיימות את התנאים הבאים:
| |
| − |
| |
| − | <math>f_{A_{1}}(x)=(x-\lambda_{1} )^{2},
| |
| − | m_{A_{1}}(x)=(x-\lambda_{1} )</math>
| |
| − |
| |
| − | מטריצה כזו הינה מהצורה: <math>\lambda _{1} I=\begin{pmatrix}
| |
| − | \lambda _{1} & 0\\
| |
| − | 0& \lambda _{1}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | והבלוק השני מגודל 1 הינו מהצורה <math>\begin{pmatrix}
| |
| − | \lambda _{2}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | ובסה"כ צורת הג'ורדן של המטריצה הינה: <math>J_{A}=J_{B}=\begin{pmatrix}
| |
| − | \lambda _{1} & 0& 0\\
| |
| − | 0& \lambda _{1} &0 \\
| |
| − | 0& 0& \lambda _{2}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | הראנו שמדובר באותה צורת ג'ורדן ולכן המטריצות A וB דומות.
| |
| − |
| |
| − |
| |
| − | '''מקרה 2:''' <math>m_{A}(x)=(x-\lambda _{1})^{2}(x-\lambda _{2})</math>
| |
| − |
| |
| − | במקרה זה הבלוקים הנוצרים (באופן זהה) הינם: <math>\begin{pmatrix}
| |
| − | \lambda _{1} & 1\\
| |
| − | 0& \lambda _{1} \\
| |
| − | \end{pmatrix}</math>
| |
| − | ו- <math>\begin{pmatrix}
| |
| − | \lambda _{2}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | ולכן צורת הג'ורדן של המטריצה הינה: <math>J_{A}=J_{B}=\begin{pmatrix}
| |
| − | \lambda _{1} & 1 & 0\\
| |
| − | 0& \lambda _{1} & 0\\
| |
| − | 0& 0& \lambda _{2}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | בסה"כ, במקרה זה לA וB אותה צורת ג'ורדן ולכן הן דומות.
| |
| − |
| |
| − |
| |
| − | '''לסיכום, הראנו שבכל מצב אפשרי המטריצות A וB דומות ומכאן שהן דומות.
| |
| − |
| |
| − | מ.ש.ל.'''
| |
| − |
| |
| − |
| |
| − | == פתרון פשוט יותר ==
| |
| − | (בלי להעביר לצורה נילפוטנטית)
| |
| | | | |
| | '''הגדרה:''' | | '''הגדרה:''' |
בסופו של דבר הראנו שהפולינום האופייני והמינימלי מגדירים באופן יחיד את צורת הג'ורדן ולכן נניח יש ל-A ול-B אתו פוינום אופיינו ומינימלי נקבל:
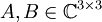 יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות
יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות  ו
ו  דומות.
דומות.
 הוא
הוא 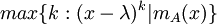
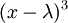 כמו שהראנו קודם
כמו שהראנו קודם
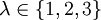
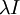 ולכן היא יחידה
ולכן היא יחידה
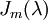 הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ
הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ 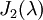 ,
,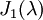
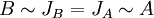
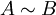
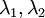 כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות :
כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות :
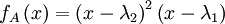
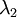
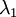 הוא 1)
ולכן יש צורת ג'ורדן יחידה אלכסונית
הוא 1)
ולכן יש צורת ג'ורדן יחידה אלכסונית
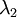 ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם:
ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם: