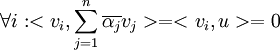פתרון לתרגיל 1.8 בחוברת לינארית
מתוך Math-Wiki
תרגיל 1.8
יהיה  ממ"פ ממימד
ממ"פ ממימד  . יהיו וקטורים
. יהיו וקטורים 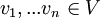 . נגדיר את מטריצת גרהם
. נגדיר את מטריצת גרהם  ע"י
ע"י 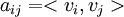 . הוכח:
. הוכח:
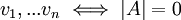 ת"ל
ת"ל
פתרון
נסתכל על צירוף לינארי כללי של עמודות  :
:
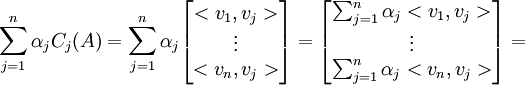
זה שווה עפ"י כמו לינאריות במשתנה שני ל
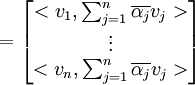
זה שווה לאפס אם
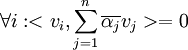
טענת עזר (נוכיח אותה מיד): 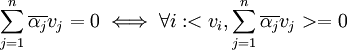
לכן הגענו למסקנה ש
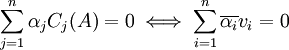
לכן
יש צירוף לינארי לא טריוויאלי של עמודות המטריצה  אם"ם יש צירוף לינארי לא טריוויאלי של הוקטורים
אם"ם יש צירוף לינארי לא טריוויאלי של הוקטורים 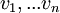 .
.
נובע מיידית ש 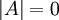
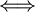 עמודות
עמודות  ת"ל
ת"ל 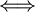 הוקטורים
הוקטורים 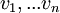 ת"ל
ת"ל
מ.ש.ל
הוכחת טענת העזר
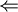
נניח
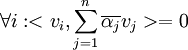
אזי גם
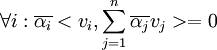
ולכן גם הסכום שלהם שווה אפס
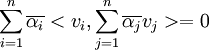
ולפי לינאריות במשתנה ראשון זה שווה
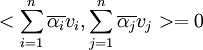
אבל הסכום בשני הצדדים הוא אותו סכום בדיוק! נסמן 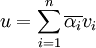 ולכן
ולכן 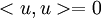 וזה נכון רק אם
וזה נכון רק אם 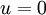 כלומר
כלומר 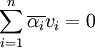
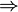
בכיוון ההפוך, נניח 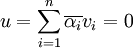 לכן ברור ש
לכן ברור ש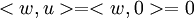 לכל וקטור
לכל וקטור 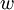 , ולכן
, ולכן