הבדלים בין גרסאות בדף "פתרון משוואה ממעלה 3"
(←שיטה שנייה (מאוחרת יותר)) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
| − | הדרך לפתרון משוואה ממעלה 3 מיוחסת | + | הדרך לפתרון משוואה ממעלה 3 מיוחסת לטארטאגליה (Tartaglia). אנו נציג שתי שיטות למצוא שורש כלשהו של המשוואה. מציאת השורשים האחרים תוסבר בסוף. |
הערה: השיטה עובדת מעל כל שדה שהמאפיין שלו אינו 2 או 3. | הערה: השיטה עובדת מעל כל שדה שהמאפיין שלו אינו 2 או 3. | ||
| + | ==לפני שמתחילים== | ||
| + | בהינתן משוואה <math>x^3+ax^2+bx+c=0</math> ניתן להציב <math>x=y-\frac{a}{3}</math> . | ||
| − | + | המשוואה שתתקבל מההצבה תהיה מהצורה <math>y^3+py+q=0</math> עבור מספרים <math>p,q</math> כלשהם. ברור כי מספיק לפתור את המשוואה ב- <math>y</math> כי <math>y=y_0</math> הוא פתרון אם ורק אם <math>x=y_0-\frac{a}{3}</math> הוא פתרון של המשוואה ב- <math>x</math> . | |
| − | + | ||
| − | '''לכן, מעכשיו נניח שהמשוואה שלנו היא מהצורה <math>y^3+py+q=0</math>.''' | + | '''לכן, מעכשיו נניח שהמשוואה שלנו היא מהצורה <math>y^3+py+q=0</math> .''' |
| − | '''הערה:''' אם מסיבה כזו או אחרת אתם יכולים לזהות בקלות שורש של המשוואה (לדוגמא, אם <math>p=0</math> או <math>q=0</math>), אל תשתמשו בשיטות לעיל. הן עלולות להיכשל בגלל חלוקה ב-0. | + | '''הערה:''' אם מסיבה כזו או אחרת אתם יכולים לזהות בקלות שורש של המשוואה (לדוגמא, אם <math>p=0</math> או <math>q=0</math>), אל תשתמשו בשיטות לעיל. הן עלולות להיכשל בגלל חלוקה ב- <math>0</math> . |
| − | == שיטה ראשונה ( | + | ==שיטה ראשונה (טארטאגליה)== |
| − | + | נחפש <math>u,v</math> כך שיתקיים | |
| − | נחפש <math>u,v</math> כך שיתקיים <math>u^3+v^3=-q</math> | + | :<math>u^3+v^3=-q</math> |
| + | :<math>uv=-\frac{p}{3}</math> . | ||
'''טענה:''' במצב זה, <math>y=u+v</math> הוא שורש של המשוואה. | '''טענה:''' במצב זה, <math>y=u+v</math> הוא שורש של המשוואה. | ||
'''הוכחה:''' נציב ונבדוק: | '''הוכחה:''' נציב ונבדוק: | ||
| + | <center><math>y^3+py+q=u^3+3u^2v+3uv^2+v^3+p(u+v)+q</math></center> | ||
| − | <math> | + | <center><math>=(u^3+v^3)+3uv(u+v)+p(u+v)+q=-q-p(u+v)+p(u+v)+q=0</math></center> |
'''מש"ל.''' | '''מש"ל.''' | ||
| − | כדי למצוא <math>u,v</math> נשים לב ש-<math>u^3\cdot v^3=-p^3 | + | כדי למצוא <math>u,v</math> נשים לב ש- <math>u^3\cdot v^3=-\frac{p^3}{27}</math> ולכן <math>u^3,v^3</math> הם שורשים של המשוואה הריבועית <math>t^2+p^3/27-q=0</math> . נשתמש בנוסחה לפתרון משוואה ריבועית כדי לקבל את הפתרונות <math>t_1,t_2</math> ואז נבחר <math>u=\sqrt[3]{t_1},v=\sqrt[3]{t_2}</math> . |
| − | + | ||
| − | == שיטה | + | ==שיטה שניה (מאוחרת יותר)== |
| + | נציב <math>y=\alpha\cos(\theta)</math> כאשר <math>\alpha=\sqrt{-\frac{4p}{3}}</math> . אם נשתמש בזהות <math>\cos(3\theta)=4\cos^3(\theta)-3\cos(\theta)</math> נקבל: | ||
| − | + | <center><math>y^3+py+q=0=\alpha^3\cos^3(\theta)+p\alpha\cos(\theta)+q=\frac{\alpha^3\bigl(\cos(3\theta)+3\cos(\theta)\bigr)}{4}-p\alpha\cos(\theta)</math></center> | |
| − | <math> | + | <center><math>=\tfrac{\alpha^3}{4}\cos(3\theta)+\alpha\left(\tfrac{3\alpha^2}{4}+p\right)\cos(\theta)+q=\tfrac{\alpha^3}{4}\cos(3\theta)+q</math></center> |
| − | לכן, מספיק למצוא <math>\theta</math> כך ש-<math>\cos 3\theta=-4q\alpha^ | + | לכן, מספיק למצוא <math>\theta</math> כך ש- <math>\cos(3\theta)=-\frac{4q}{\alpha^3}</math> כדי ש- <math>y=\alpha\cos(\theta)</math> יהיה פתרון. |
| − | בדרך כלל נצטרך להשתמש ב-<math>\arccos</math> מרוכב כדי לחלץ את <math>3\theta</math> ואז נצטרך להפעיל <math>\cos</math> מרוכב על <math>\theta</math> (כי הוא כנראה יהיה מספר מרוכב). | + | בדרך כלל נצטרך להשתמש ב- <math>\arccos</math> מרוכב כדי לחלץ את <math>3\theta</math> ואז נצטרך להפעיל <math>\cos</math> מרוכב על <math>\theta</math> (כי הוא כנראה יהיה מספר מרוכב). |
גרסה אחרונה מ־17:20, 6 ביוני 2016
הדרך לפתרון משוואה ממעלה 3 מיוחסת לטארטאגליה (Tartaglia). אנו נציג שתי שיטות למצוא שורש כלשהו של המשוואה. מציאת השורשים האחרים תוסבר בסוף.
הערה: השיטה עובדת מעל כל שדה שהמאפיין שלו אינו 2 או 3.
לפני שמתחילים
בהינתן משוואה 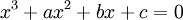 ניתן להציב
ניתן להציב 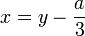 .
.
המשוואה שתתקבל מההצבה תהיה מהצורה 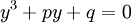 עבור מספרים
עבור מספרים 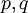 כלשהם. ברור כי מספיק לפתור את המשוואה ב-
כלשהם. ברור כי מספיק לפתור את המשוואה ב-  כי
כי 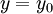 הוא פתרון אם ורק אם
הוא פתרון אם ורק אם 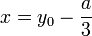 הוא פתרון של המשוואה ב-
הוא פתרון של המשוואה ב-  .
.
לכן, מעכשיו נניח שהמשוואה שלנו היא מהצורה 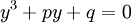 .
.
הערה: אם מסיבה כזו או אחרת אתם יכולים לזהות בקלות שורש של המשוואה (לדוגמא, אם 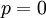 או
או 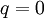 ), אל תשתמשו בשיטות לעיל. הן עלולות להיכשל בגלל חלוקה ב-
), אל תשתמשו בשיטות לעיל. הן עלולות להיכשל בגלל חלוקה ב-  .
.
שיטה ראשונה (טארטאגליה)
נחפש 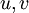 כך שיתקיים
כך שיתקיים
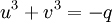
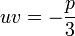 .
.
טענה: במצב זה, 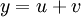 הוא שורש של המשוואה.
הוא שורש של המשוואה.
הוכחה: נציב ונבדוק:
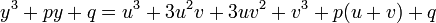
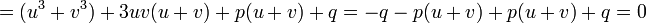
מש"ל.
כדי למצוא 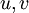 נשים לב ש-
נשים לב ש- 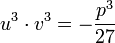 ולכן
ולכן 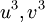 הם שורשים של המשוואה הריבועית
הם שורשים של המשוואה הריבועית 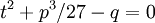 . נשתמש בנוסחה לפתרון משוואה ריבועית כדי לקבל את הפתרונות
. נשתמש בנוסחה לפתרון משוואה ריבועית כדי לקבל את הפתרונות 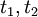 ואז נבחר
ואז נבחר ![u=\sqrt[3]{t_1},v=\sqrt[3]{t_2}](/images/math/b/4/7/b47159b520f02596a47127b912b5ca12.png) .
.
שיטה שניה (מאוחרת יותר)
נציב 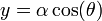 כאשר
כאשר 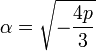 . אם נשתמש בזהות
. אם נשתמש בזהות 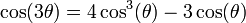 נקבל:
נקבל:
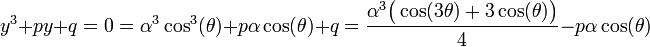
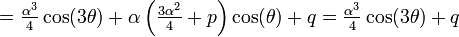
לכן, מספיק למצוא 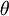 כך ש-
כך ש- 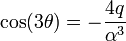 כדי ש-
כדי ש- 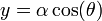 יהיה פתרון.
בדרך כלל נצטרך להשתמש ב-
יהיה פתרון.
בדרך כלל נצטרך להשתמש ב- 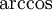 מרוכב כדי לחלץ את
מרוכב כדי לחלץ את 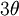 ואז נצטרך להפעיל
ואז נצטרך להפעיל 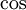 מרוכב על
מרוכב על 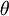 (כי הוא כנראה יהיה מספר מרוכב).
(כי הוא כנראה יהיה מספר מרוכב).