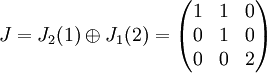הבדלים בין גרסאות בדף "פתרון 4 (אלעד איטח)"
(יצירת דף עם התוכן "א. אחרי חישובים נקבל שהפולינום האופייני של A הוא <math>f_{A}(x)=\left | xI-A \right |=(x-1)^{2}(x-2)</math> ב. לפולינ...") |
Noamlifshitz (שיחה | תרומות) |
||
| שורה 2: | שורה 2: | ||
ב. לפולינום המינימאלי של A יש אותם גורמים אי-פריקים כמו לפולינום האופייני של A. | ב. לפולינום המינימאלי של A יש אותם גורמים אי-פריקים כמו לפולינום האופייני של A. | ||
| − | אחרי חישוב נקבל ש- <math>A-I)(A-2I)\neq 0 </math> כלומר, לא קיים פולינום ממעלה נמוכה יותר מזו של הפולינום האופייני של A | + | אחרי חישוב נקבל ש- <math>(A-I)(A-2I)\neq 0 </math> כלומר, לא קיים פולינום ממעלה נמוכה יותר מזו של הפולינום האופייני של A |
שיש לו אותם גורמים אי-פריקים שמאפס את A. הפולינום האופייני של A הוא פולינום מתוקן ומהמעלה הנמוכה ביותר שמאפס את A (לפי משפט קיילי-המילטון). | שיש לו אותם גורמים אי-פריקים שמאפס את A. הפולינום האופייני של A הוא פולינום מתוקן ומהמעלה הנמוכה ביותר שמאפס את A (לפי משפט קיילי-המילטון). | ||
לכן הפולינום המינימאלי של A הוא <math>m_{A}(x)=f_{A}(x)=(x-1)^{2}(x-2)</math> | לכן הפולינום המינימאלי של A הוא <math>m_{A}(x)=f_{A}(x)=(x-1)^{2}(x-2)</math> | ||
גרסה מ־09:05, 4 בינואר 2012
א. אחרי חישובים נקבל שהפולינום האופייני של A הוא 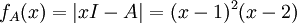
ב. לפולינום המינימאלי של A יש אותם גורמים אי-פריקים כמו לפולינום האופייני של A.
אחרי חישוב נקבל ש- 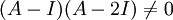 כלומר, לא קיים פולינום ממעלה נמוכה יותר מזו של הפולינום האופייני של A
שיש לו אותם גורמים אי-פריקים שמאפס את A. הפולינום האופייני של A הוא פולינום מתוקן ומהמעלה הנמוכה ביותר שמאפס את A (לפי משפט קיילי-המילטון).
לכן הפולינום המינימאלי של A הוא
כלומר, לא קיים פולינום ממעלה נמוכה יותר מזו של הפולינום האופייני של A
שיש לו אותם גורמים אי-פריקים שמאפס את A. הפולינום האופייני של A הוא פולינום מתוקן ומהמעלה הנמוכה ביותר שמאפס את A (לפי משפט קיילי-המילטון).
לכן הפולינום המינימאלי של A הוא 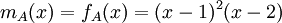 ג. הע"ע של A הם שורשי הפולינום האופייני של A, שהם 2 ו-1.
ג. הע"ע של A הם שורשי הפולינום האופייני של A, שהם 2 ו-1.
ד. נגדיר 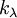 -הריבוי האלגברי של ע"ע למדה ו-
-הריבוי האלגברי של ע"ע למדה ו-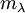 הריבוי הגיאומטרי שלו.
הריבוי האלגברי של ע"ע למדה מוגדר בתור האינדקס הגדול ביותר k שעבורו
הריבוי הגיאומטרי שלו.
הריבוי האלגברי של ע"ע למדה מוגדר בתור האינדקס הגדול ביותר k שעבורו 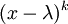 מחלק את הפולינום האופייני של A. לכן,
מחלק את הפולינום האופייני של A. לכן, 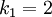
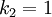 הריבוי הגיאומטרי של כל ע"ע קטן או
שווה לריבוי האלגברי שלו וגם גדול או שווה ל-1. לכן,
הריבוי הגיאומטרי של כל ע"ע קטן או
שווה לריבוי האלגברי שלו וגם גדול או שווה ל-1. לכן, 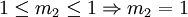 הריבוי הגיאומטרי של ע"ע מוגדר בתור המימד של המרחב העצמי המתאים לע"ע זה. לפיכך,
הריבוי הגיאומטרי של ע"ע מוגדר בתור המימד של המרחב העצמי המתאים לע"ע זה. לפיכך, 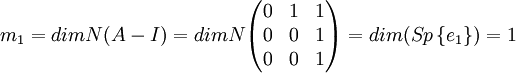
ה.הפולינום האופייני של A מתפרק לגורמים ליניאריים, ולכן קיימת צורת ז'ורדן ל-A.
מס' הבלוקים הקשורים לכל ע"ע שווה לריבוי הגיאומטרי שלו, ולכן לכל אחד מהע"ע יש בלוק אחד.
A היא מסדר 3, ולכן צורת הז'ורדן שלה היא מסדר 3, והיא מכילה בלוק מסדר 2 ובלוק מסדר 1.
הסדר של הבלוק הגדול ביותר (ובמקרה זה, גם היחיד) של כל ע"ע למדה הוא החזקה של הגורם 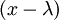 בפולינום המינימאלי של A. לכן, הבלוק הקשור לע"ע 2 הוא מסדר 1 והבלוק הקשור לע"ע 1 הוא מסדר 2.
לסיכום, צורת הז'ורדן של A היא
בפולינום המינימאלי של A. לכן, הבלוק הקשור לע"ע 2 הוא מסדר 1 והבלוק הקשור לע"ע 1 הוא מסדר 2.
לסיכום, צורת הז'ורדן של A היא