פתרונות לקורס לינארית 2 לתיכוניסטים תש"ע - תרגיל 3
מתוך Math-Wiki
תרגיל 3
5.21
ניתן דוגמאות נגדיות לכל הסעיפים:
א. 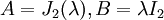
ב. 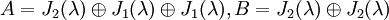
- איך אנו יודעים שהן לא דומות ללא משפט ז'ורדן? מכיוון שהריבוי הגיאומטרי של
 שונה בין שתי המטריצות (בA הוא 3 ובB הוא 2. קל לראות את זה מחישוב ישיר של המרחב העצמי).
שונה בין שתי המטריצות (בA הוא 3 ובB הוא 2. קל לראות את זה מחישוב ישיר של המרחב העצמי). - מדוע הריבוי הגיאומטרי חייב להיות שווה בין מטריצות דומות? כי מטריצה הדומה למטריצה אחרת למעשה מייצגת את אותו האופרטור רק בשינוי קואורדינטות. לכן מימד המרחב העצמי חייב להיות זהה, רק הוקטור משתנה (כי הוא למעשה אותו וקטור רק בקואורדינטות אחרות.
ג.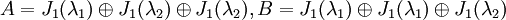
5.22
א.
- נתון
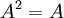 לכן ברור ש
לכן ברור ש 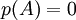 עבור
עבור 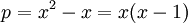 .
. - הפולינום המינימלי מחלק כל פולינום שמאפס את המטריצה לכן הפולינום המינימלי הוא
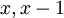 או
או 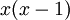
- אם
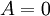 אזי
אזי 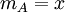 . אם
. אם 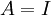 אזי
אזי 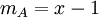 . אף מטריצה אחרת לא מאפסת את שני הפולינום האלה, לכן עבור כל מטריצה אחרת
. אף מטריצה אחרת לא מאפסת את שני הפולינום האלה, לכן עבור כל מטריצה אחרת 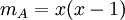
ב.
- הע"ע מאפסים את הפולינום המינימלי ולכן האופציות הן 0 ו/או 1.
ג.
- הפירוק נתון כבר בסעיף א'.
ד.
- הפולינום המינימלי מתפרק לגורמים לינאריים, לכן המטריצה ניתנת לשילוש, לכן היא דומה למטריצה משולשית שעל האלכסון שלה נמצאים הע"ע של המטריצה.
- אם
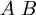 אזי
אזי 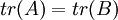 הוכחה: למדנו ש
הוכחה: למדנו ש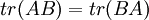 . לכן אם
. לכן אם 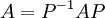 אז
אז 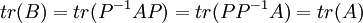
- לכן
 דומה למטריצה משולשית
דומה למטריצה משולשית 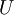 ולכן
ולכן 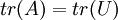 . האלכסון של
. האלכסון של 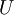 בנוי מאחדות ואפסים, והאורך שלו הוא
בנוי מאחדות ואפסים, והאורך שלו הוא  . לכן
. לכן