הבדלים בין גרסאות בדף "שדות - תכונות בסיסיות"
מתוך Math-Wiki
(יצירת דף עם התוכן " == איברים אלגבריים וטרנסצנדנטיים == '''הגדרה:''' יהיה <math>F</math> שדה. הרחבה של <math>F</math> היא כינוי...") |
|||
| שורה 1: | שורה 1: | ||
| − | |||
== איברים אלגבריים וטרנסצנדנטיים == | == איברים אלגבריים וטרנסצנדנטיים == | ||
| שורה 5: | שורה 4: | ||
'''הגדרה:''' יהיה <math>F</math> שדה. הרחבה של <math>F</math> היא כינוי לכל שדה <math>K</math> המכיל את <math>F</math>. לרוב כותבים גם <math>L/K</math>. | '''הגדרה:''' יהיה <math>F</math> שדה. הרחבה של <math>F</math> היא כינוי לכל שדה <math>K</math> המכיל את <math>F</math>. לרוב כותבים גם <math>L/K</math>. | ||
| − | אם <math>K/F</math> היא הרחבת שדות, אז באופן טבעי <math>K</math> הוא מרחב וקטורי מעל <math>F</math>. המימד של <math>K</math> מעל <math>F</math> יסומן ב-<math>[K:F]</math>. | + | אם <math>K/F</math> היא הרחבת שדות, אז באופן טבעי <math>K</math> הוא מרחב וקטורי מעל <math>F</math>. המימד של <math>K</math> מעל <math>F</math> יסומן ב-<math>[K:F]</math> (הוא אינו חייב להיות סופי). |
| + | |||
| + | '''טענה ("נוסחת המכפלה"):''' יהיו <math>F\subseteq K\subseteq L</math> שדות. אזי <math>[L:F]=[L:K]\cdot[K:F]</math>. | ||
| + | |||
| + | '''הרעיון של ההוכחה:''' אם <math>A</math> הוא בסיס ל-<math>L</math> כמרחב וקטורי מעל <math>K</math> ו-<math>B</math> הוא בסיס ל-<math>K</math> כמרחב וקטורי מעל <math>F</math> אז הקבוצה <math>\{ab~|~a\in A, b\in B\}</math> היא בסיס ל-<math>L</math> כמרחב וקטורי מעל <math>F</math> והיא בעלת <math>[L:K][K:F]</math> איברים (זה לא טריוויאלי). | ||
| + | |||
'''הגדרה:''' תהי <math>K/F</math> הרחבת שדות ו-<math>a\in K</math>. האיבר <math>a</math> נקרא אלגברי מעל <math>F</math> אם קיים פולינום <math>f(x)</math> כך ש-<math>f(a)=0</math>. אם לא קיים פולינום כזה, <math>a</math> נקרא טרנסצנדנטי מעל <math>F</math>. | '''הגדרה:''' תהי <math>K/F</math> הרחבת שדות ו-<math>a\in K</math>. האיבר <math>a</math> נקרא אלגברי מעל <math>F</math> אם קיים פולינום <math>f(x)</math> כך ש-<math>f(a)=0</math>. אם לא קיים פולינום כזה, <math>a</math> נקרא טרנסצנדנטי מעל <math>F</math>. | ||
גרסה מ־14:45, 24 בנובמבר 2011
איברים אלגבריים וטרנסצנדנטיים
הגדרה: יהיה  שדה. הרחבה של
שדה. הרחבה של  היא כינוי לכל שדה
היא כינוי לכל שדה  המכיל את
המכיל את  . לרוב כותבים גם
. לרוב כותבים גם 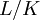 .
.
אם 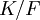 היא הרחבת שדות, אז באופן טבעי
היא הרחבת שדות, אז באופן טבעי  הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל  . המימד של
. המימד של  מעל
מעל  יסומן ב-
יסומן ב-![[K:F]](/images/math/5/9/f/59f3c52d355ea1c639439971525b4478.png) (הוא אינו חייב להיות סופי).
(הוא אינו חייב להיות סופי).
טענה ("נוסחת המכפלה"): יהיו 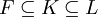 שדות. אזי
שדות. אזי ![[L:F]=[L:K]\cdot[K:F]](/images/math/a/9/5/a95da03d6476c4b99059aec6796d0a8c.png) .
.
הרעיון של ההוכחה: אם  הוא בסיס ל-
הוא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  ו-
ו- הוא בסיס ל-
הוא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  אז הקבוצה
אז הקבוצה 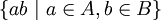 היא בסיס ל-
היא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  והיא בעלת
והיא בעלת ![[L:K][K:F]](/images/math/f/f/f/fff655cf82db99fc56717c5530ac013b.png) איברים (זה לא טריוויאלי).
איברים (זה לא טריוויאלי).
הגדרה: תהי 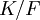 הרחבת שדות ו-
הרחבת שדות ו-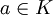 . האיבר
. האיבר  נקרא אלגברי מעל
נקרא אלגברי מעל  אם קיים פולינום
אם קיים פולינום  כך ש-
כך ש-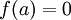 . אם לא קיים פולינום כזה,
. אם לא קיים פולינום כזה,  נקרא טרנסצנדנטי מעל
נקרא טרנסצנדנטי מעל  .
.