הבדלים בין גרסאות בדף "שדות - תכונות בסיסיות"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏איברים אלגבריים וטרנסצנדנטיים)
(←‏הרחבות של שדות)
שורה 12: שורה 12:
 
'''תכונה:''' אם <math>F</math> שדה אז כל חיתוך של תתי שדות של <math>F</math> הוא גם שדה.
 
'''תכונה:''' אם <math>F</math> שדה אז כל חיתוך של תתי שדות של <math>F</math> הוא גם שדה.
  
−
'''הגדרה:''' נניח ש-<math>L</math> שדה ו-<math>F,K</math> תת שדות של <math>L</math>. הקומפוזיטום של <math>F,K</math> הוא תת השדה הקטן ביותר המכיל את <math>F,K</math>. הוא יסומן ב-<math>LK</math>.
+
'''הגדרה:''' נניח ש-<math>L</math> שדה ו-<math>F,K</math> תת שדות של <math>L</math>. הקומפוזיטום של <math>F,K</math> הוא תת השדה הקטן ביותר המכיל את <math>F,K</math>. הוא יסומן ב-<math>FK</math>.
−
 
+
−
 
+
  
 
== איברים אלגבריים וטרנסצנדנטים ==
 
== איברים אלגבריים וטרנסצנדנטים ==

גרסה מ־15:02, 24 בנובמבר 2011

הרחבות של שדות

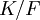הגדרה: יהיה F שדה. הרחבה של F היא כינוי לכל שדה K המכיל את F. לרוב כותבים גם K/F. באופן טבעי K הוא מרחב וקטורי מעל F. המימד של K מעל F יסומן ב-[K:F] (הוא אינו חייב להיות סופי).

דוגמא: 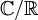\mathbb{C}/\mathbb{R} היא הרחבת שדות ממימד סופי. 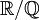\mathbb{R}/\mathbb{Q} היא הרחבת שדות ממימד אינסופי.

טענה: יהיו 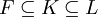F\subseteq K\subseteq L שדות. אזי [L:F]=[L:K]\cdot[K:F].

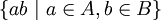הרעיון של ההוכחה: אם A הוא בסיס ל-L כמרחב וקטורי מעל K ו-B הוא בסיס ל-K כמרחב וקטורי מעל F אז הקבוצה \{ab~|~a\in A, b\in B\} היא בסיס ל-L כמרחב וקטורי מעל F והיא בעלת [L:K][K:F] איברים (זה לא טריוויאלי).

תכונה: אם F שדה אז כל חיתוך של תתי שדות של F הוא גם שדה.

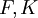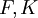הגדרה: נניח ש-L שדה ו-F,K תת שדות של L. הקומפוזיטום של F,K הוא תת השדה הקטן ביותר המכיל את 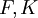F,K. הוא יסומן ב-FK.

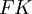איברים אלגבריים וטרנסצנדנטים

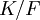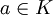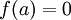הגדרה: תהי K/F הרחבת שדות ו-a\in K. האיבר a נקרא אלגברי מעל F אם קיים פולינום f(x) כך ש-f(a)=0. אם לא קיים פולינום כזה, a נקרא טרנסצנדנטי מעל F.

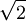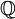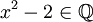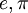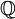דוגמא: \sqrt{2} הוא אלגברי מעל \mathbb{Q} כי הוא מאפס את x^2-2\in\mathbb{Q}. לעומת זאת, ניתן להוכיח כי המספרים e,\pi הם טרנסצנדנטיים מעל \mathbb{Q}.

הערה: לא קשה להראות כי כמות המספרים המרוכבים האלגבריים מעל 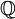\mathbb{Q} היא בת מנייה. לכן, בהכרח קיימים ב-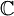\mathbb{C} (וגם ב-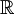\mathbb{R}) איברים טרנסצנדנטיים. (זו הוכחה לא קונסטרוקטיבית לכך שקיימים מספרים טרנצנדנטיים).

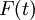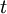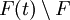דוגמא: יהיה F שדה ויהי F(t) שדה השברים של F[t]. קל לבדוק כי t טרנסצנדנטי מעל F. למעשה, כל איבר ב-F(t)\setminus F הוא טרנסצנדנטי.

מקור: https://math-wiki.com/index.php?title=שדות_-_תכונות_בסיסיות&oldid=16327