הבדלים בין גרסאות בדף "שדות - תכונות בסיסיות"
(←איברים אלגבריים - מבט מעמיק) |
|||
| שורה 45: | שורה 45: | ||
== תרגילים - כדי לראות שהבנתם עד עכשיו == | == תרגילים - כדי לראות שהבנתם עד עכשיו == | ||
| − | '''תרגיל:''' תהי <math>L/F</math> הרחבת שדות ו-<math>a_1,\ldots,a_n\in L</math> אלגבריים מעל <math>F</math>. הראו כי <math>F[a_1,\ldots,a_n]</math> שדה. הראו כי זה תת השדה הקטן ביותר המכיל את <math>F</math> ואת <math>a_1,\ldots,a_n</math>. (הערה: <math>F[a_1,\ldots,a_n]</math> מוגדר באופן אינדוקטיבי ע"י <math>F[a_1,\ldots,a_n]=F[a_1,\ldots,a_{n-1}][a_n]</math>. קיימות גם הגדרות שקולות אחרות.) | + | '''תרגיל:''' תהי <math>L/F</math> הרחבת שדות ו-<math>a_1,\ldots,a_n\in L</math> אלגבריים מעל <math>F</math>. הראו כי <math>F[a_1,\ldots,a_n]</math> שדה והמימד שלו מעל <math>F</math> סופי. הראו כי זה תת השדה הקטן ביותר המכיל את <math>F</math> ואת <math>a_1,\ldots,a_n</math>. (הערה: <math>F[a_1,\ldots,a_n]</math> מוגדר באופן אינדוקטיבי ע"י <math>F[a_1,\ldots,a_n]=F[a_1,\ldots,a_{n-1}][a_n]</math>. קיימות גם הגדרות שקולות אחרות.) |
'''תרגיל:''' תהי <math>L/F</math> הרחבת שדות, <math>a_1,\ldots,a_n\in L</math> אלגבריים מעל <math>F</math> ו-<math>F\subseteq K\subseteq L</math>. הוכיחו כי הקומפוזיטום של <math>F[a_1,\ldots,a_n]</math> ו-<math>K</math> הוא <math>K[a_1,\ldots,a_n]</math>. | '''תרגיל:''' תהי <math>L/F</math> הרחבת שדות, <math>a_1,\ldots,a_n\in L</math> אלגבריים מעל <math>F</math> ו-<math>F\subseteq K\subseteq L</math>. הוכיחו כי הקומפוזיטום של <math>F[a_1,\ldots,a_n]</math> ו-<math>K</math> הוא <math>K[a_1,\ldots,a_n]</math>. | ||
| שורה 62: | שורה 62: | ||
'''דוגמא:''' לפי מה שעכשיו הראינו, אוסף האיברים האלגבריים מעל <math>\mathbb{Q}</math> ב-<math>\mathbb{C}</math> הוא שדה. (למעשה, זה הסגור האלגברי של <math>\mathbb{Q}</math>.) | '''דוגמא:''' לפי מה שעכשיו הראינו, אוסף האיברים האלגבריים מעל <math>\mathbb{Q}</math> ב-<math>\mathbb{C}</math> הוא שדה. (למעשה, זה הסגור האלגברי של <math>\mathbb{Q}</math>.) | ||
| + | |||
| + | '''דוגמא:''' יהי <math>F</math> שדה ויהי <math>K=F(t)</math> (שדה השברים של <math>F[t]</math> = שדה הפונקציות הרציונליות במשתנה <math>t</math>). אזי האיברים האלגבריים מעל <math>K</math> הם רק השדה <math>F</math>. | ||
| + | |||
| + | '''טענה:''' יהיו <math>F\subseteq K\subseteq L</math> שדות כך ש-<math>K/F</math> הרחבה אלגברית. אזי איבר <math>a\in L</math> הוא אלגברי מעל <math>K</math> אם ורק אם הוא אלגברי הוא אלגברי מעל <math>F</math>. | ||
| + | |||
| + | '''הוכחה:''' כוון אחד ברור מאליו -- אם <math>a</math> אלגברי מעל <math>F</math> אז הוא גם אלגברי מעל <math>K</math>. הכוון השני לא טריוויאלי. נניח ש-<math>a</math> אלגברי מעל <math>K</math> אזי קיים פולינום <math>0\neq f(x)\in K[x]</math> כך ש-<math>f(a)=0</math>. יהיו <math>b_0,b_1,b_2,\ldots,b_n\in K</math> מקדמי הפולינום <math>f</math>. היות ו-<math>K/F</math> הרחבה אלגברית, אז כל האיברים <math>b_0,b_1,\ldots,b_n</math> אלגבריים מעל <math>F</math>. לכן, לפי תרגיל מקודם, <math>K_0=F[b_0,\ldots,b_n]</math> הוא שדה ממימד סופי מעל <math>F</math>. בנוסף, <math>f(x)\in K_0[x]</math> ולכן <math>a</math> אלגברי מעל <math>K_0</math>. לפי טענה ממקודם, זה אומר ש-<math>[K_0[a]:K_0]<\infty</math>. לכן <math>[K_0[a]:F]=[K_0[a]:K_0]\cdot [K_0:F]<\infty</math>. לפי מסקנה מקודם, זה אומר שההרחבה <math>K_0[a]/F</math> אלגברית ולכן <math>a</math> אלגברי מעל <math>F</math>. | ||
| + | |||
| + | '''הערה:''' בהוכחה היינו צריכים להגדיר את <math>K_0</math> כי לא היה נתון ש-<math>[K:F]<\infty</math>. | ||
גרסה מ־10:54, 25 בנובמבר 2011
תוכן עניינים
הרחבות של שדות
הגדרה: יהיה  שדה. הרחבה של
שדה. הרחבה של  היא כינוי לכל שדה
היא כינוי לכל שדה  המכיל את
המכיל את  . לרוב כותבים גם
. לרוב כותבים גם 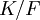 . באופן טבעי
. באופן טבעי  הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל  . המימד של
. המימד של  מעל
מעל  יסומן ב-
יסומן ב-![[K:F]](/images/math/5/9/f/59f3c52d355ea1c639439971525b4478.png) (הוא אינו חייב להיות סופי).
(הוא אינו חייב להיות סופי).
דוגמא: 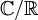 היא הרחבת שדות ממימד סופי.
היא הרחבת שדות ממימד סופי. 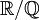 היא הרחבת שדות ממימד אינסופי.
היא הרחבת שדות ממימד אינסופי.
טענה: יהיו 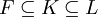 שדות. אזי
שדות. אזי ![[L:F]=[L:K]\cdot[K:F]](/images/math/a/9/5/a95da03d6476c4b99059aec6796d0a8c.png) .
.
הרעיון של ההוכחה: אם  הוא בסיס ל-
הוא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  ו-
ו- הוא בסיס ל-
הוא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  אז הקבוצה
אז הקבוצה 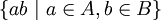 היא בסיס ל-
היא בסיס ל- כמרחב וקטורי מעל
כמרחב וקטורי מעל  והיא בעלת
והיא בעלת ![[L:K][K:F]](/images/math/f/f/f/fff655cf82db99fc56717c5530ac013b.png) איברים (זה לא טריוויאלי).
איברים (זה לא טריוויאלי).
תכונה: אם  שדה אז כל חיתוך של תתי שדות של
שדה אז כל חיתוך של תתי שדות של  הוא גם שדה.
הוא גם שדה.
הגדרה: נניח ש- שדה ו-
שדה ו-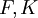 תת שדות של
תת שדות של  . הקומפוזיטום של
. הקומפוזיטום של 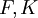 הוא תת השדה הקטן ביותר המכיל את
הוא תת השדה הקטן ביותר המכיל את 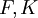 . הוא יסומן ב-
. הוא יסומן ב-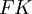 .
.
איברים אלגבריים וטרנסצנדנטים
הגדרה: תהי 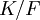 הרחבת שדות ו-
הרחבת שדות ו-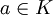 . האיבר
. האיבר  נקרא אלגברי מעל
נקרא אלגברי מעל  אם קיים פולינום
אם קיים פולינום 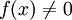 כך ש-
כך ש-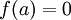 . אם לא קיים פולינום כזה,
. אם לא קיים פולינום כזה,  נקרא טרנסצנדנטי מעל
נקרא טרנסצנדנטי מעל  .
.
דוגמא: 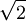 הוא אלגברי מעל
הוא אלגברי מעל 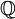 כי הוא מאפס את
כי הוא מאפס את 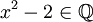 . לעומת זאת, ניתן להוכיח כי המספרים
. לעומת זאת, ניתן להוכיח כי המספרים 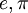 הם טרנסצנדנטיים מעל
הם טרנסצנדנטיים מעל 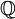 .
.
הערה: לא קשה להראות כי כמות המספרים המרוכבים האלגבריים מעל 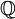 היא בת מנייה. לכן, בהכרח קיימים ב-
היא בת מנייה. לכן, בהכרח קיימים ב-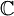 (וגם ב-
(וגם ב-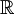 ) איברים טרנסצנדנטיים. (זו הוכחה לא קונסטרוקטיבית לכך שקיימים מספרים טרנצנדנטיים).
) איברים טרנסצנדנטיים. (זו הוכחה לא קונסטרוקטיבית לכך שקיימים מספרים טרנצנדנטיים).
דוגמא: יהיה  שדה ויהי
שדה ויהי 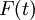 שדה השברים של
שדה השברים של ![F[t]](/images/math/c/7/7/c7724caea94513d8a26fba05263d2996.png) . קל לבדוק כי
. קל לבדוק כי 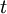 טרנסצנדנטי מעל
טרנסצנדנטי מעל  . למעשה, כל איבר ב-
. למעשה, כל איבר ב-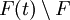 הוא טרנסצנדנטי.
הוא טרנסצנדנטי.
הערה: אם 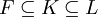 שדות ו-
שדות ו-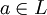 אלגברי מעל
אלגברי מעל  אז הוא גם אלגברי מעל
אז הוא גם אלגברי מעל  . (נובע ישירות ע"י שימוש בהגדרה מכך ש-
. (נובע ישירות ע"י שימוש בהגדרה מכך ש-![F[x]\subseteq K[x]](/images/math/0/9/7/097db3a258f42d0cbb4b020c2c79db9c.png) .)
.)
הגדרה: הרחבת שדות 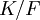 נקראת אלגברית אם כל איבר ב-
נקראת אלגברית אם כל איבר ב- אלגברי מעל
אלגברי מעל  .
.
סימון: תהי 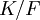 הרחבת שדות ו-
הרחבת שדות ו-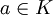 . מסמנים
. מסמנים ![F[a]=\{f(a)~|~f\in F[x]\}](/images/math/f/1/0/f106dc5930d6628418eec3b6f3b1c85d.png) .
.
טענה: תהי 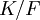 הרחבת שדות ו-
הרחבת שדות ו-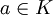 . אזי
. אזי  אלגברי מעל
אלגברי מעל  אם ורק אם המימד של
אם ורק אם המימד של ![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) כמרחב וקטורי מעל
כמרחב וקטורי מעל  סופי. במקרה זה
סופי. במקרה זה ![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) שדה.
שדה.
הוכחה: כוון אחד: נניח ש-![\dim_FF[a]=n<\infty](/images/math/8/4/d/84d1d168885182f7f532d75dd49df906.png) . אזי הקבוצה
. אזי הקבוצה 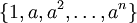 היא בגודל
היא בגודל  ולכן תלויה לינארית מעל
ולכן תלויה לינארית מעל  . לכן קיימים
. לכן קיימים 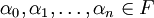 , לא כולם 0, כך ש-
, לא כולם 0, כך ש-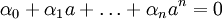 . אם נגדיר
. אם נגדיר ![f(x)=\alpha_0+\alpha_1x+\ldots+\alpha_nx^n\in F[x]](/images/math/c/c/7/cc7746d2c2cd1288c8ced3b4dd2965ce.png) אז
אז 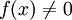 ובעצם הראינו
ובעצם הראינו 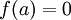 . לכן
. לכן  אלגברי מעל
אלגברי מעל  .
.
כוון שני: נניח שקיים 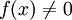 כך ש-
כך ש-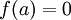 . נסמן
. נסמן
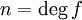 . מספיק להראות ש-
. מספיק להראות ש-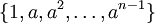 קבוצה פורשת (מעל
קבוצה פורשת (מעל  ) ל-
) ל-![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) . יהי
. יהי ![b\in F[a]](/images/math/9/e/a/9eae7fd7789f6f5a3ddd69f05df1ac51.png) אזי
אזי 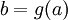 עבור
עבור ![g(x)\in F[x]](/images/math/e/8/a/e8a6f386186ed748e56a9d481f6b418d.png) כלשהו. קיימים פולינומים
כלשהו. קיימים פולינומים ![q(x),r(x)\in F[x]](/images/math/e/1/e/e1eeb1f7fb12b709a3c977f94ecf2352.png) כך ש-
כך ש-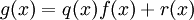 וגם
וגם 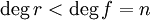 . אזי
. אזי 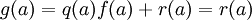 ו-
ו-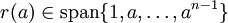 כי
כי 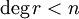 .
.
כדי לראות שבמקרה זה ![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) שדה, נשים לב ש-
שדה, נשים לב ש-![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) הוא תחום שלמות ממימד סופי מעל
הוא תחום שלמות ממימד סופי מעל  ולכן סיימנו הודות לתרגיל הבא:
ולכן סיימנו הודות לתרגיל הבא:
תרגיל: יהי  תחום שלמות ו-
תחום שלמות ו-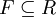 שדה כך ש-
שדה כך ש-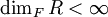 . אזי
. אזי  שדה. [רמז: לכל
שדה. [רמז: לכל 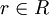 ההעתקה
ההעתקה 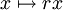 היא העתקה לינארית חד חד ערכית (מדוע?).]
היא העתקה לינארית חד חד ערכית (מדוע?).]
מסקנה: אם 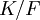 הרחבת שדות ממעלה סופית (כלומר
הרחבת שדות ממעלה סופית (כלומר ![[K:F]<\infty](/images/math/f/b/f/fbf19b862a78c2eefb5fbbdc0b427bb2.png) היא הרחבה אלגברית.
היא הרחבה אלגברית.
תרגילים - כדי לראות שהבנתם עד עכשיו
תרגיל: תהי 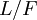 הרחבת שדות ו-
הרחבת שדות ו-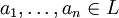 אלגבריים מעל
אלגבריים מעל  . הראו כי
. הראו כי ![F[a_1,\ldots,a_n]](/images/math/a/3/d/a3d29ded52d4eab01a1e5ec1eaddbc5b.png) שדה והמימד שלו מעל
שדה והמימד שלו מעל  סופי. הראו כי זה תת השדה הקטן ביותר המכיל את
סופי. הראו כי זה תת השדה הקטן ביותר המכיל את  ואת
ואת 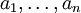 . (הערה:
. (הערה: ![F[a_1,\ldots,a_n]](/images/math/a/3/d/a3d29ded52d4eab01a1e5ec1eaddbc5b.png) מוגדר באופן אינדוקטיבי ע"י
מוגדר באופן אינדוקטיבי ע"י ![F[a_1,\ldots,a_n]=F[a_1,\ldots,a_{n-1}][a_n]](/images/math/e/5/8/e58dbdcb96da1f05f59a8879e4789a8e.png) . קיימות גם הגדרות שקולות אחרות.)
. קיימות גם הגדרות שקולות אחרות.)
תרגיל: תהי 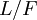 הרחבת שדות,
הרחבת שדות, 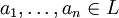 אלגבריים מעל
אלגבריים מעל  ו-
ו-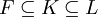 . הוכיחו כי הקומפוזיטום של
. הוכיחו כי הקומפוזיטום של ![F[a_1,\ldots,a_n]](/images/math/a/3/d/a3d29ded52d4eab01a1e5ec1eaddbc5b.png) ו-
ו- הוא
הוא ![K[a_1,\ldots,a_n]](/images/math/b/4/2/b424bada0552d7f95c3902e4499cc4cd.png) .
.
איברים אלגבריים - מבט מעמיק
טענת עזר: תהי 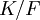 הרחבת שדות ו-
הרחבת שדות ו-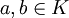 אלגבריים. אזי
אלגבריים. אזי ![F[a,b]/F](/images/math/e/e/5/ee57c4617f8dba11f862896ffc191f85.png) הרחבה אלגברית.
הרחבה אלגברית.
הוכחה: לפי טענה מקודם מספיק להראות ש-![[F[a,b]:F]<\infty](/images/math/d/c/1/dc1406369c2a672bbc0aff5018e9c6d2.png) . מתקיים
. מתקיים ![[F[a,b]:F]=[F[a,b]:F[a]]\cdot [F[a]:F]](/images/math/6/7/f/67f03f8970b9fa85d98958387b308714.png) ולכן מספיק להראות סופיות של כל אחד מהגורמים במכפלה. לפי אותה טענה
ולכן מספיק להראות סופיות של כל אחד מהגורמים במכפלה. לפי אותה טענה ![[F[a]:F]<\infty](/images/math/4/5/1/45143dd94d04d408d468735318c9b4d8.png) כי
כי  אלגברי מעל
אלגברי מעל  . בנוסף,
. בנוסף, 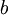 אלגברי מעל
אלגברי מעל  ולכן גם מעל
ולכן גם מעל ![F[a]](/images/math/2/9/3/2934f44c838546efd120d1d9071425fa.png) . כעת, אותה טענה גם אומרת כי
. כעת, אותה טענה גם אומרת כי ![[F[a,b]:F[a]]<\infty](/images/math/d/b/f/dbffb8c947c8e2b8ba528aff0c81b24c.png) ולכן גמרנו.
ולכן גמרנו.
מסקנה: אם 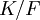 הרחבת שדות ו-
הרחבת שדות ו-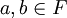 אלגבריים מעל
אלגבריים מעל  , אז גם
, אז גם 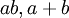 אלגבריים מעל
אלגבריים מעל  .
.
תרגיל: בהנחות של המסקנה, אם 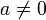 אז גם
אז גם 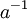 אלגברי.
אלגברי.
מסקנה: תהי 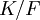 הרחבת שדות. נסמן ב-
הרחבת שדות. נסמן ב- את כל האיברים ב-
את כל האיברים ב- שאלגבריים מעל
שאלגבריים מעל  . אזי
. אזי  שדה. למעשה,
שדה. למעשה,  הוא תת השדה הגדול ביותר של
הוא תת השדה הגדול ביותר של  שאלגברי מעל
שאלגברי מעל  .
.
דוגמא: לפי מה שעכשיו הראינו, אוסף האיברים האלגבריים מעל 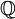 ב-
ב-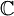 הוא שדה. (למעשה, זה הסגור האלגברי של
הוא שדה. (למעשה, זה הסגור האלגברי של 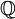 .)
.)
דוגמא: יהי  שדה ויהי
שדה ויהי 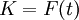 (שדה השברים של
(שדה השברים של ![F[t]](/images/math/c/7/7/c7724caea94513d8a26fba05263d2996.png) = שדה הפונקציות הרציונליות במשתנה
= שדה הפונקציות הרציונליות במשתנה 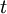 ). אזי האיברים האלגבריים מעל
). אזי האיברים האלגבריים מעל  הם רק השדה
הם רק השדה  .
.
טענה: יהיו 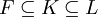 שדות כך ש-
שדות כך ש-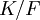 הרחבה אלגברית. אזי איבר
הרחבה אלגברית. אזי איבר 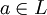 הוא אלגברי מעל
הוא אלגברי מעל  אם ורק אם הוא אלגברי הוא אלגברי מעל
אם ורק אם הוא אלגברי הוא אלגברי מעל  .
.
הוכחה: כוון אחד ברור מאליו -- אם  אלגברי מעל
אלגברי מעל  אז הוא גם אלגברי מעל
אז הוא גם אלגברי מעל  . הכוון השני לא טריוויאלי. נניח ש-
. הכוון השני לא טריוויאלי. נניח ש- אלגברי מעל
אלגברי מעל  אזי קיים פולינום
אזי קיים פולינום ![0\neq f(x)\in K[x]](/images/math/7/0/c/70c08ba251a2cbd7f572594796c98276.png) כך ש-
כך ש-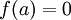 . יהיו
. יהיו 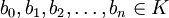 מקדמי הפולינום
מקדמי הפולינום  . היות ו-
. היות ו-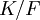 הרחבה אלגברית, אז כל האיברים
הרחבה אלגברית, אז כל האיברים 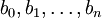 אלגבריים מעל
אלגבריים מעל  . לכן, לפי תרגיל מקודם,
. לכן, לפי תרגיל מקודם, ![K_0=F[b_0,\ldots,b_n]](/images/math/e/b/d/ebd7f56829efbc8127282ad510f7f189.png) הוא שדה ממימד סופי מעל
הוא שדה ממימד סופי מעל  . בנוסף,
. בנוסף, ![f(x)\in K_0[x]](/images/math/a/f/f/aff14275bd913c474733ad530021ef39.png) ולכן
ולכן  אלגברי מעל
אלגברי מעל 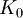 . לפי טענה ממקודם, זה אומר ש-
. לפי טענה ממקודם, זה אומר ש-![[K_0[a]:K_0]<\infty](/images/math/8/2/6/82661301e99443dec99894297b48c0d6.png) . לכן
. לכן ![[K_0[a]:F]=[K_0[a]:K_0]\cdot [K_0:F]<\infty](/images/math/0/9/1/091a27be35de322bf410bfa5f8ed3bc5.png) . לפי מסקנה מקודם, זה אומר שההרחבה
. לפי מסקנה מקודם, זה אומר שההרחבה ![K_0[a]/F](/images/math/e/9/1/e91de0cd66f0f0d390993db894231a63.png) אלגברית ולכן
אלגברית ולכן  אלגברי מעל
אלגברי מעל  .
.
הערה: בהוכחה היינו צריכים להגדיר את 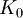 כי לא היה נתון ש-
כי לא היה נתון ש-![[K:F]<\infty](/images/math/f/b/f/fbf19b862a78c2eefb5fbbdc0b427bb2.png) .
.