גרסה מ־20:51, 23 בפברואר 2012

3.3

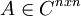שאלת תלמיד: בהוכחה אפשר לקחת באופן מפורש $\epsilon=\frac{1}{2}min\left \{ [A\cdot |v|]_{i} \right \}_{1 \leq i\leq n }$ , נכון? (כאשר $A \in C^{nxn}$ )

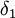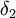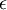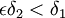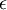תשובה: הרבה יותר קל לחשוב קונספטואלית (בלי חישובים): נתונים שני וקטורים, האחד חיובי והשני אי-שלילי. ניקח את האיבר הקטן ביותר של הוקטור החיובי, נניח שהוא $\delta_1$ . ניקח את האיבר הגדול ביותר של הוקטור האי-שלילי, נקרא לו $\delta_2$ . ברור שיש $\epsilon$ כך ש $\epsilon\delta_2 < \delta_1$ , וממילא כל רכיבי הוקטור השני, אחרי שנכפילם ב $\epsilon$ , יהיו קטנים יותר מכל רכיבי הוקטור הראשון.

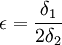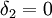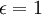אם אתה מתעקש על משהו של ממש, ניקח למשל $\epsilon=\frac{\delta_1}{2\delta_2}$ , ואם $\delta_2=0$ אז ניקח למשל $\epsilon=1$ .

@@ שורה 8: / שורה 8: @@
 <math>\delta_2</math>. ברור שיש <math>\epsilon</math> כך ש
 <math>\epsilon\delta_2 < \delta_1 </math>,
- וממילא כל רכיבי הוקטור השני, אחרי שנכפילם ב <math>\epsilon</math>, יהיו קטנים יותר מכל רכיבי הוקטור הראשון.
+וממילא כל רכיבי הוקטור השני, אחרי שנכפילם ב <math>\epsilon</math>, יהיו קטנים יותר מכל רכיבי הוקטור הראשון.
 אם אתה מתעקש על משהו של ממש, ניקח למשל <math>\epsilon=\frac{\delta_1}{2\delta_2}</math>, ואם <math>\delta_2=0</math> אז ניקח למשל <math>\epsilon=1</math>.

הבדלים בין גרסאות בדף "שיחה:הסודות של גוגל"

גרסה מ־20:51, 23 בפברואר 2012

3.3

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים