גרסה מ־15:08, 23 בנובמבר 2013

חזרה לדף הקורס

גלול לתחתית העמוד

תוכן עניינים

1 הוספת שאלה חדשה
2 שאלות

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

שאלות

שאלה על תרגיל 1 מהמערכת של moodle

אני נכנסתי אל תוך המערכת ורציתי לראות אילו תרגילים קיבלנו בתור ש"ב כאשר שנכנסתי בפעם השנייה לתרגיל1 המערכת אומרת ומציעה אופצייה "המשך את הניסיון האחרון " השאלה שלי היא אם אני אלחץ על הכפתור-אני לא יוכל יותר להיכנס כמה פעמיים שאני ארצה עד לפני סוף הגשה? אשמח לתשובה

אתה יכול להיכנס כמה פעמים שאתה רוצה עד שאתה מגיש.

כשאתה מגיש את התרגיל המערכת מודיעה לך בצורה ברורה שזו הגשה סופית ולא תוכל לשנות יותר ושואלת אותך האם אתה בטוח שאתה רוצה להגיש.

חוץ מזה, את תרגיל 1 ספציפית המערכת נותנת לכם להגיש כמה פעמים שאתם רוצים - בדיוק בשביל זה. אל תפחדו לעשות טעויות השבוע, תשחקו עם המערכת כדי להכיר אותה.

--איתמר שטיין 10:10, 15 באוקטובר 2013 (IDT)

הארכת מועד ההגשה באינפי

שלום,

אני תלמיד של ד"ר הורוביץ שלא הספיק להשלים את שיעורי הבית במועד שצוין (29/10 18:00). במהלך סוף השבוע , אתר ה"מודל" היה מושבת וכתוצאה מכך רבים נאלצו להמתין, דבר שגזל את זמן הכנת השיעורים. בנוסף, תרגילי הבית של המרצים האחרים (ביתן ואגרונובסקי) הוארכו לעוד מספר ימים.

לאחראים על האתר , אנא מכם האריכו את מועד ההגשה לעוד מספר ימים.

תודה

שתיי שאלות

1. למה בין כל שניי מספרים, קיים מספר רציונלי? 2. איך מוכיחים שלכל מספר ממשי x, קיימת סדרת רציונליים שמתכנסת אליו? ולמה ניתן לבחור את הסדרה עולה או יורדת?

תודה מראש!!!!

תשובה:

1. זה לא משפט טריוויאלי. מוכיחים אותו עם עקרון ארכימדס.

בסיכומי הרצאות שנמצאות כאן עקרון ארכימדס מופיע בסוף ההרצאה הראשונה וההוכחה לטענה מופיעה בתחילת ההרצאה השניה.

אם יש דברים לא ברורים בהוכחה שם תשאל שוב ואני אענה.

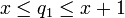2. אחרי שאתה כבר יודע שבין כל שני מספרים קיים מספר רציונאלי אתה עושה ככה: נניח ש $x$ זה המספר הממשי שלנו. אז קיים מספר רציונאלי $x\leq q_1 \leq x+1$ זה האיבר הראשון של הסדרה.

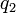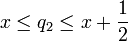עכשיו נבחר מספר רציונאלי $q_2$ כך ש $x \leq q_2 \leq x+ \frac{1}{2}$ זה האיבר השני.

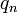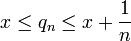וכך הלאה נבחר את $q_n$ כך ש $x \leq q_n \leq x+ \frac{1}{n}$ .

אז נקבל שהסדרה 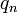$q_n$ היא סדרה של רציונאלים שמתכנסת ל $x$ .

אפשר להכריח את הסדרה להיות יורדת, אם למשל בוחרים

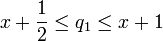
$x+\frac{1}{2} \leq q_1 \leq x+1$

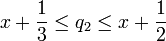
$x+\frac{1}{3} \leq q_2 \leq x+\frac{1}{2}$

וכן הלאה

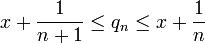$x+\frac{1}{n+1} \leq q_n \leq x+\frac{1}{n}$ .

ובדומה אפשר להכריח אותה להיות עולה אם בוחרים

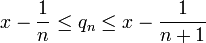$x-\frac{1}{n} \leq q_n \leq x-\frac{1}{n+1}$ .

מקווה שזה ברור --איתמר שטיין (שיחה) 06:32, 7 בנובמבר 2013 (EST)

תודה רבה על התשובה...בכל אופן יש לי שאלה לגבי ההוכחה שהצעת כאן. בהחלט נראה שהסדרות שנתת כאן מתכנסות ל-x. אבל לא אמורים להוכיח את זה איכשהו? מה שכתבת מהווה הוכחה? כי זה נראה לי כמו לטעון שהסדרה 1 חלקי n מתכנסת ל-0, מבלי להוכיח זאת. אפשר להוכיח את מה שכתבת איכשהו? זו צריכה להיות הוכחה בכתיב אפסילון, לא?

תשובה: נכון. זה לא מהווה הוכחה שזה מתכנס. כדי להוכיח צריך באמת להשתמש בכתיב 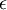$\epsilon$ וכו'. אבל את זה קל לעשות במקרה הזה.

בשלב מסוים נתחיל להשמיט טיעונים כאלה שקל להשלים.--איתמר שטיין (שיחה) 07:33, 11 בנובמבר 2013 (EST)

ש"ב

אני תלמיד של ד"ר ביתן ובתשובות בשיעורי הבית מספר 3 רשמתי בתשובה 1- והוא רשם לי טעות ושהתשובה הנכונה היא -1 האם אפשר בבקשה לתקן לי את הציון?

כן, תשלח לי מייל (Steinita@walla.com) עם השם שלך וכתובת המייל שאיתה נרשמת ל moodle.

בפעם הבאה תלחץ LeftCntrl+Shift לפני הזנת תשובה מספרית כדי שזה יהיה משמאל לימין.

--איתמר שטיין (שיחה) 01:05, 8 בנובמבר 2013 (EST)

שאלה לגבי הוכחת המשפט : מתכנסת ==>חסומה

הוכחתי את המשפט כך: נניח an מתכנסת לגבול L

לכן לכל e>o קיים n0 טבעי כך שלכל n>n0 :

zz |an-L|<e zz לכן zz L-e<an<L+e zz.

ניקח את zz M = max{a1,a2,...,an0,L+e} zz ו- zz m = min{a1,a2,...,L-e} zz

לכן לכל n טבעי מתקיים: zz m<an<M zz.

ראיתי פתרון לשאלה הזו שבה בחרו את אפסילון להיות 1.

( זה הפתרון: http://math-wiki.com/images/2/21/Sol3Infi12011.pdf#page=1&zoom=auto,0,810 )

בהוכחה שלי, כפי שניתן לראות, לא בחרתי אפסילון ספציפי.

הבדל נוסף בין הפתרון שלי לפתרון המצורף, הוא שכתוב שם, "קיים n0 כך ש...", ואז כתוב: "ניקח n1>n0...".

גם את זה לא עשיתי...עבדתי רק עם n0.

האם ההבדלים שניי ההבדלים הללו בין הפתרון שלי לפתרון המצורף הם הבדלים מהותיים? או שגם הפתרון שלי קביל?

אם יש משמעות להבדלים הללו, אשמח להסבר.

לגבי n1 שהופיע שם נראה לי שהוא פשוט נובע מכך שהגדרת הגבול שהתייחסו אליה שם היא .... לכל

n>n_0

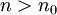ולא גדול או שווה. בהנחה שעובדים עם ההגדרה השקולה להתכנסות שבה יש גדול או שווה אפשר לעבוד רק עם n0.

לגבי השאלה השניה קבוצה היא חסומה אם קיים.... לאור העובדה שבהגדרת הגבול יש את העניין של לכל אפסילון צריך לבחור אפסילון מסויים זה יכול להיות אחד וזה יכול להיות אפסילון שרירותי אבל מה שבטוח משתמשים כאן בכך שאם טענה מסוימת מתקיימת לכל איבר בקבוצה לא ריקה אז קיים איבר בקבוצה שהטענה מתקיימת לגביו. לצורך הענין אם בהגדרת הגבול היה רשום לכל אפסילון ששייך לקבוצה מסוימת ולא היה ברור אם הקבוצה ריקה או לא אי אפשר היה לעבור מטענת לכל לטענת קיים. בקיצור 1 לא חשוב אבל צריך להגיד משהו על המעבר בין לכל לקיים.--מני (שיחה) 11:57, 10 בנובמבר 2013 (EST)

תרגיל-רוני ביתן:ההוכחה בין שאלה 8 לשאלה 9

האם זה לא נובע ישירות ממשפט בולצאנו ווירשטראס?

לא שאני רואה. אני אסביר שוב מה הטענה אומרת: ברור שקבוצת הגבולות החלקיים חסומה. ולכן ברור שיש לה חסם עליון ותחתון

אבל זה בכלל לא ברור למה החסמים העליון והתחתון עצמם הם גבולות חלקיים (למה שתהיה סדרה שמתכנסת אליהם?)--איתמר שטיין (שיחה) 07:41, 11 בנובמבר 2013 (EST)

תרגיל 4 של רוני ביתן שאלה 10

ניסיתי לשלול אפשרויות בעזרת מקרה פרטי של סדרה מתכנסת,האם קיימת דרך של הוכחה המסתמכת על המשפטים שלמדנו?

לשלול אפשרויות בעזרת מקרים פרטיים זה רעיון טוב. אבל כל טענה נכונה שיש בתרגילי הבית - אפשר להוכיח אותה ישירות בעזרת הכלים שיש לכם (בלי להסתמך על זה ששוללים את כל האחרים).--איתמר שטיין (שיחה) 07:36, 11 בנובמבר 2013 (EST)

-אני אנסח מחדש,מהי דרך ההוכחה לתרגיל הזה,מה הפתרון כביכול

תשובה: נראה לי שהכי נוח לחשוב על זה בצורה טופולגית.

אתה יודע שגבולות חלקיים של $a_n$ זה נקודות הצטברות של הקבוצה. הגבול החלקי העליון זאת נקודת ההצטברות הכי גדולה.

לקחת את 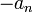$-a_n$ זה פשוט לעשות שיקוף סביב $0$ . ואז קל להבין מה יוצא הגבול העליון של $a_n$ .

מה שכתבתי כאן זה לא הוכחה כמובן, רק האינטואיציה - הוכחה מלאה תופיע בתשובות על התרגיל.--איתמר שטיין (שיחה) 03:33, 15 בנובמבר 2013 (EST)

דיוק אחרי הנקודה העשרונית בכתיבת תשובות

בתרגיל החמישי של ד"ר ביתן יש מספר גבולות שהם חזקות של e, שאחד מהם יוצא מספר הקטן מ-0.01 וכתוב דיוק של שתי ספרות אחרי הנקודה, אז פשוט לכתוב 0? --Omer rosler (שיחה) 15:19, 17 בנובמבר 2013 (EST)

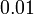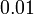תשובה: אם יוצאת לך תשובה קטנה מ $0.01$ אז גם $0$ וגם $0.01$ יתקבלו ע"י המערכת.--איתמר שטיין (שיחה) 01:01, 18 בנובמבר 2013 (EST)

האם מבחני ההתכנסות דו כיווניים?

למשל,אם ידוע שטור An מתכנס אז האם אני יכול לאמר שהגבול של |An+1\An| קטן מ1?(לפי מבחן דלמבר)

לא, למשל 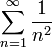$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}$ מתכנס אבל הגבול של 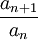$\frac{a_{n+1}}{a_n}$ הוא 1.--איתמר שטיין (שיחה) 01:02, 18 בנובמבר 2013 (EST)

קריטריון קושי להתכנסות סדרה

האם אני יכול לעשות בקריטריון קושי על נוסחת נסיגה רדוקציה של |Am-An| ל|An+1-An|? מכיוון שm תמיד גדול או שווה לn+1 (עבור m גדול מn(

אם הבנתי אותך נכון - אז כן.

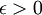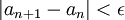במילים אחרות: אם אתה יודע שקריטריון קושי מתקיים. אתה יודע גם שלכל $\epsilon>0$ , החל משלב מסוים בסדרה מתקיים $|a_{n+1}-a_n|<\epsilon$ .

אבל: ההפך לא נכון. אם אתה יודע שלכל 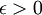$\epsilon>0$ , החל משלב מסוים בסדרה מתקיים 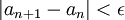$|a_{n+1}-a_n|<\epsilon$ - זה לא אומר שקריטריון קושי מתקיים וזה לא אומר שהסדרה מתכנסת.--איתמר שטיין (שיחה) 01:06, 18 בנובמבר 2013 (EST)

תרגיל 6 של רוני ביתן שאלה 1

השאלה הזו הופיעה בתרגיל הקודם עבור טור חיובי,אפשרי להשתמש במה שידוע לנו על הטור החיובי לגבי הטור הכללי?(האם קיימת דרך הוכחה כזו)

אתה יכול להניח שאתה יודע שזה נכון עבור טורים חיוביים. אבל שים לב שזה נכון עבור טורים חיוביים לפי מבחן ההשוואה.

ומבחן ההשוואה לא עובד בשביל טורים כללים.--איתמר שטיין (שיחה) 03:57, 19 בנובמבר 2013 (EST)

שאלה

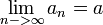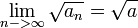נתון: $\lim_{n->\infty}a_n{}=a$ הוכח: $\lim_{n->\infty}\sqrt{a_n{}}=\sqrt{a}$ .

ארשום את ההוכחה. יש לי שאלה לגבי מעבר מסוים בהוכחה:

עיבוד הנוסחה נכשל (שגיאת תחביר): \left | \sqrt{a_n{}} \right -\sqrt{a}|=\left | (\sqrt{a_n{}}-\sqrt{a})(\sqrt{a_n{}}+

כעת, מה שאני רוצה לומר, זה ש-

@@ שורה 186: / שורה 186: @@
 ארשום את ההוכחה. יש לי שאלה לגבי מעבר מסוים בהוכחה:
+  <math>\left | \sqrt{a_n{}} \right -\sqrt{a}|=\left | (\sqrt{a_n{}}-\sqrt{a})(\sqrt{a_n{}}+</math>
-  <math>\left | \sqrt{a_n{}} \right -\sqrt{a}|=\left | (\sqrt{a_n{}}-\sqrt{a})(\sqrt{a_n{}}+\sqrt{a})/(\sqrt{a_n{}}+\sqrt{a})|=\left | (a_n{}-a)/(\sqrt{a_n{}}+\sqrt{a}) \right |\leq \left | a_n{}-a \right |\cdot 1/\sqrt{a}</math>
 כעת, מה שאני רוצה לומר, זה ש-

הבדלים בין גרסאות בדף "שיחה:88-132 אינפי 1 סמסטר א' תשעד"

גרסה מ־15:08, 23 בנובמבר 2013

תוכן עניינים

הוספת שאלה חדשה

שאלות

שאלה על תרגיל 1 מהמערכת של moodle

הארכת מועד ההגשה באינפי

שתיי שאלות

ש"ב

שאלה לגבי הוכחת המשפט : מתכנסת ==>חסומה

תרגיל-רוני ביתן:ההוכחה בין שאלה 8 לשאלה 9

תרגיל 4 של רוני ביתן שאלה 10

דיוק אחרי הנקודה העשרונית בכתיבת תשובות

האם מבחני ההתכנסות דו כיווניים?

קריטריון קושי להתכנסות סדרה

תרגיל 6 של רוני ביתן שאלה 1

שאלה

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים