תקציר שימושי מחשב, סמסטר ב תשעג, גיא בלשר
תאריך עדכון אחרון: 29 ביוני 2013
תוכן עניינים
תוכנה 1: MATLAB
הערה: ב־MATLAB בסוף כך שורת הוראה יש להוסיף ; על מנת שלא תתבצע הדפסה, אך אם רוצים הדפסה אין להוסיף ; בסוף השורה.
עבודה בסיסית ב־MATLAB
משתנים
משתנה הוא סמל המסמן כמות, איבר של קבוצה, או ערך לוגי, העשויים להשתנות (מתוך ויקיפדיה).
השמה למשתנה - הכנסת ערך אליו. ב־MATLAB (דוגמות):
x=3
z=pi
w=4+5*i
פעולות בסיסיות עם משתנים (a,b מציינים מספרים):
| הפעולה | הסימן ב־MATLAB |
|---|---|
| חיבור | a+b |
| חיסור | a-b |
| כפל | a*b |
| חילוק | / |
| חזקה | a^b |
| לוגריתם טבעי (ln) | (log(a |
| שורש ריבועי | (sqrt(a |
| ערך שלם / רצפה | (floor(a |
| שארית חלוקה (רק עבור שלמים) | (mod(a,b |
להוספת הערה בסוף שורה כותבים את הסימן % ולאחריו את ההערה.
בחילוק שני מספרים שלמים, המנה היא (floor(x,y והשארית היא (mod(x,y.
משתנים קבועים: i,j - ה־i המרוכב, 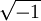 , pi - פאי.
, pi - פאי.
הדפסת ערך משתנה:
(disp(value
מטריצות
פעולות בסיסיות עם משתנים (A,B מציינים מטריצות):
| הפעולה | ההוראה ב־MATLAB |
|---|---|
הגדרת מטריצת אפסים בגודל 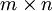
|
(A=zeros(m,n |
| איבר בשורה x ובעמודה y | (A(x,y |
| חיבור מטריצות | A+B |
| חיסור מטריצות | A-B |
| כפל במובן מטריצות | A*B |
| כפל איבר־איבר | A.*B |
| חילוק (כפל בהופכית) | A/B |
| חילוק איבר־איבר | A./B |
| מימדי מטריצה (וקטור) | (size(A |
| שחלוף (transpose) | 'A |
ועוד...
הערה 1: האינדקסים במטריצה מתחילים מ־1.
הערה 2: אם נעשתה פנייה לאיבר שאינו במערך והושם בו ערך, MATLAB ירחיב באופן אוטומטי את המערך, ובמקומות שנוספו יושמו אפסים.
מערכים: מטריצה מגודל nx1
פעולות בסיסיות עם מערכים (v מייצג וקטור, m,n,p מייצגים מספר כלשהו):
| הפעולה | ההוראה ב־MATLAB |
|---|---|
| אתחול (הצבת אפסים) | (v=zeros(n,1 |
| האיבר ה־n-י | (v(n |
| אורך הוקטור | (length(v |
| וקטור המכיל את המספרים הטבעיים עד n | v=1:n |
| וקטור המכיל את כל המספרים מ־m עד n בקפיצות p | v=m:p:n |
דוגמה: בכתיבה 1:5 יווצר הווקטור [5 4 3 2 1]. בכתיבה 1:2:5 יווצר הוקטור [5 3 1].
ניתן להגדיר וקטור גם באופן הבא: [w=[3 9 10 11 4 (במקום רווחים ניתן להשתמש בפסיקים). על מנת להגדיר מטריצה באופן דומה מוסיפים ; כדי לרדת שורה.
ניתן לקבל וקטור מאינדקסים מסוימים. למשל, עבור w שהוגדר,
[w(1:2:5)=w([1 3 5])=[3 10 4
פעולות בוליאניות
פעולות בוליאניות מחזירות 0 (שקר) או 1 (אמת). דוגמות (a,b מספרים):
| הפעולה | הסימון ב־MATLAB |
|---|---|
| האם שני ערכים שווים | a==b |
| קטן | ab |
| קטן שווה | a<=b |
| גדול שווה | a>=b |
| אינו שווה | =~ |
&& - וגם, || - או
תנאים
תנאי פשוט:
(תנאי) if
הוראות לביצוע
end
תנאי מורכב:
(תנאי) if
(הוראות לביצוע)
else
(הוראות לביצוע)
end
תנאי יותר מורכב:
(תנאי) if
(הוראות לביצוע)
elseif
(הוראות לביצוע)
else
(הוראות לביצוע)
end
לולאת for
לולאת for - ביצוע אותו רצף הוראות מספר ידוע מראש של פעמים.
תכנות:
(וקטור המכיל את ערכי i הדרושים)=for i
(הוראות לביצוע)
end
הערה: אמנם i הוא קבוע, אך ניתן להציב בו ערך. על מנת להחזירו להיות ה־i המרוכב, נכתוב את ההוראה clear i.
לולאת while
לולאת while - ביצוע אותו רצף הוראות מספר שאינו ידוע מראש של פעמים אך עם תנאי לעצירה.
תכנות:
(תנאי לעצירה, תנאי בוליאני) while
(הוראות לביצוע)
end
תרגילים
תרגיל 1 - עצרת
חשבו את 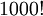 .
.
פתרון 1 - לולאת for:
;n=1 for i=2:1000 ;n=n*i end ;(disp(n
פתרון 2 - לולאת while:
;n=1 ;i=1 while i<=1000 ;n=n*i ;i=i+1 end ;(disp(n
תרגיל 2 - מספרים ראשוניים
צרו וקטור המכיל את כל המספרים הראשוניים מ־1 עד 1000
;כמה ראשוניים מצאנו % found=0
;וקטור עם המספרים הראשוניים % []=primes
for p=1:1000
;yesno=1
;k=2
while k<=sqrt(p) && yesno==1
if mod(p,k)==0
;yesno=0
end
;k=k+1
end
if yesno==1
;found=found+1
;primes(found)=p
end
end
תרגיל 3 - פירוק מספר שלם לגורמים ראשוניים
פרקו מספר שלם 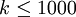 לגורמים ראשוניים (אפשר להשתמש בוקטור primes מהתרגיל הקודם).
לגורמים ראשוניים (אפשר להשתמש בוקטור primes מהתרגיל הקודם).
;k=252
while k>1
;i=2
while mod(k,primes(i))!~=0
;i=i+1
end
;((disp(primes(i
;(k=k/primes(i
end
יישומים מתמטיים
מחלק משותף גדול ביותר gcd
עבור 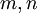 שלמים, המספר השלם הגדול ביותר המחלק גם את
שלמים, המספר השלם הגדול ביותר המחלק גם את 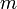 וגם את
וגם את  ייקרא המחלק המשותף הגדול ביותר ויסומן
ייקרא המחלק המשותף הגדול ביותר ויסומן 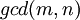 .
.
;m=12
;n=30
if n<m
;t=m
;m=n
;n=t
end
for i=1:m
if mod(m,i)==0 && mod(n,i)=0
;gcd=i
end
end
;(disp(gcd
קבלת מינימום
ישנן שלוש דרכים לקבל את המספר המינימלי מבין 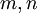 .
.
דרך ראשונה - ([min([m,n
דרך שנייה - תנאי
דרך שלישית - 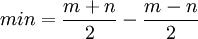
אלגוריתם אוקלידס
אלגוריתם אוקלידס נועד למציאת מחלק משותף מקסימלי בין שני מספרים שלמים 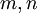 .
.
האלגוריתם
נניח 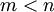 . נגדיר:
. נגדיר:
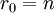
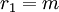
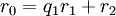 כאשר
כאשר 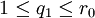 ,
, 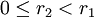
ובאינדוקציה 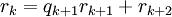
עד שנגיע ל־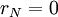 .
.
בהכרח נעצור כי 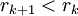 .
.
לפי אלגוריתם זה, ה־gcd הינו 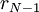 .
.
דוגמה
נבחר 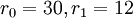 .
.
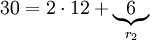
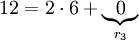
ולכן 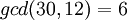
הוכחת האלגוריתם
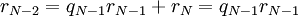
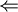
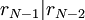 .
.
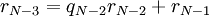 .
.
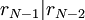 וגם
וגם 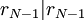
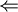
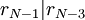
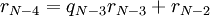 .
.
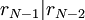 וגם
וגם 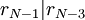
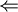
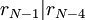
<BR
באינדוקציה, נקבל 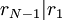 וגם
וגם 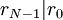 .
.
מדוע 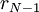 הוא המחלק המשותף הגדול ביותר? נניח
הוא המחלק המשותף הגדול ביותר? נניח 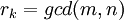 , אזי
, אזי 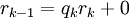 .
.
בהכרח נגיע למחלק המשותף המקסימלי מפני שבשלב ה־k־י, 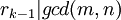 וגם
וגם 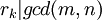 , לכן
, לכן 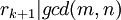 .
.
תכנות
;m=12 ;n=30 if n<m ;r1=n ;r0=m else ;r1=m ;r0=n end while r1>0 ;(r2=mod(r0,r1 ;r0=r1 ;r1=r2 end ;gcd=r0
דוגמה
עבור 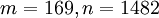
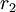
|
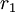
|
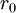
|
|---|---|---|
| 169 | 1482 | |
| 130 | 130 | 169 |
| 39 | 39 | 130 |
| 13 | 13 | 39 |
| 0 | 0 | 13 |
gcd(169,1482)=13
עבור 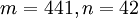
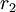
|
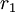
|
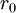
|
|---|---|---|
| 42 | 441 | |
| 21 | 21 | 42 |
| 0 | 0 | 21 |
gcd(42,441)=21
פתרון מערכת משוואות - ניוטון-רפסון
תהי  פונקציה, צריך למצוא
פונקציה, צריך למצוא  כך ש־
כך ש־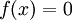 .
.
האלגוריתם והוכחתו
נתחיל מנקודה כלשהי, ובכל פעם נעביר דרכה משיק ונקבל נקודה חדשה - ששיעור ה־x שלה זהה לשיעור ה־x של החיתוך עם ציר x של המשיק. המחשת האלגוריתם
נתון  . נחשב את משוואת הישר
. נחשב את משוואת הישר 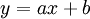 ,
, 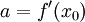 , עובר בנקודה
, עובר בנקודה 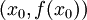 (משוואת המשיק):
(משוואת המשיק):
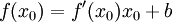
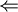
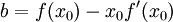
כלומר, הישר המשיק ל־ הינו
הינו 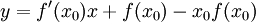 . נמצא את
. נמצא את 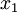 . חיתוך עם ציר
. חיתוך עם ציר  :
:
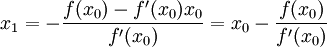 .
.
לכן, 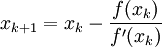 . נמשיך באיטרציות עד ש־
. נמשיך באיטרציות עד ש־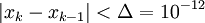
טענה: 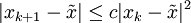 עבור
עבור 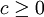 , כאשר
, כאשר 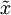 הינו השורש האמיתי.
הינו השורש האמיתי.
תכנות
נתונה פונקציה f ופונקציה 'g=f. השגיאה הרצויה delta.
;x0=1 ;x1=x0+2*delta while abs(x0-x1)>delta ;(x1=x0-f(x0)/g(x0 ;t=x1 ;x1=x0 ;x0=t end
פונקציות
פונקציה הינה רצף הוראות שנועד להתבצע עם נתונים מסוימים. למשל, פונקציה יכולה לקבל מספר ולהדפיס האם הוא ראשוני. פונקציה יכולה להחזיר ערך (או מערך עם כמה ערכים) או לא להחזיר ערך.
תכנות ב־MATLAB:
(קלט) שם הפונקציה = [פלט] function (הוראות לביצוע) end
תרגילים
תרגיל 1 - האם ראשוני
כתבו פונקציה שתקבל מספר טבעי 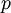 . הפונקציה תחזיר 1 אם הוא ראשוני ו־0 אחרת.
. הפונקציה תחזיר 1 אם הוא ראשוני ו־0 אחרת.
(function [yn]=isprime(p
;yn=1
;k=2
while k<=sqrt(p) && yn==1
if mod(p,k)==0
;yn=0
end
;k=k+1
end
end
בהסתמך על הפונקציה הנ"ל, כתבו תוכנית שתיצור וקטור של המספרים הראשוניים עד למספר טבעי נתון  .
.
;[]=primes
;0=found
for k=1:n
1==(if isprime(k
;found=found+1
;primes(found)=k
end
end
תרגיל 2 - האם וקטור הוא פרמוטציה (תמורה)
כתבו פונקציה המקבלת וקטור ובודקת אם הוא פרמוטציה של 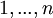 .
.
(function [yn] = ispermut (v
;(n=length(v
;(found=zeros(n,1
for i=1:n
;yn=1
if v(i)<1 || v(i)>n
;yn=0
else
;found(v(i))=1
end
end
;sum=0
for i=1:n
;(sum=sum+found(i
end
;(yn=(sum==n
end
מבני נתונים
המטרה: לכתוב פונקציות להוספה, למחיקה, לחיפוש ולמיון במערך. נחלק את הפעולות לשני מקרים: המערך אינו ממוין והמערך ממוין.
מערך שאינו ממוין
נגדיר איזשהו מערך:
;[v=[79,100,31,5,84
ונבצע עליו את הפעולות הבאות:
הוספה
(function [u] = add2array (v,k הפונקציה מוסיפה איבר k למערך v ומחזירה u % ;u=v ;u(end+1)=k end
מחיקה
אפשרות 1:
(function [u] = deleteFromArray (v,p הפונקציה מוחקת את האיבר ה־p־י במערך ומחזירה u % ;(u=zeros(length(v)-1,1 ;(u(1:p-1)=v(1:p-1 ;(u(p:length(v)-1)=v(p+1:end end
אפשרות 2:
(function [u] = deleteFromArray2 (v,p הפונקציה מוחקת את האיבר ה־p־י במערך ומחזירה u % ;(u=zeros(length(v)-1,1 for i=1:p-1 ;(u(i)=v(i end (for i=p+1:length(v ;(u(i-1)=v(i end end
חיפוש
(function [p] = findInArray (v,x
הפונקציה מחזירה את המקום במערך שבו x נמצא או אפס אם x אינו במערך %
;k=1
;p=0
;(n=length(v
while p==0 && k<=n
if v(k)==x
;p=k
else
;k=k+1
end
end
end
מערך ממוין
כעת נניח שיש לנו מערך ממוין v, למשל מהקטן לגדול.
מחיקה
בדיוק כמו במערך שאינו ממוין.
חיפוש
ישנן שתי שיטות חיפוש: חיפוש בינארי ואריה במדבר.
חיפוש בינארי:
(function [p] = binarySearch (v,x
;(n=length(v
;L=1
;H=n
while L<H-1
;(M=floor((L+H)/2
(if x<v(M
;H=M
else
;L=M
end
end
(if x==v(H
;p=H
else
;p=L
end
end
מספר הפעולות בחיפוש בינארי: 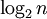
הוספה
אם x קטן מ־(v(1, נכניס אותו בהתחלה. אחרת נחפש את x ונכניס אותו אחרי L.
מיון פשוט
ראשית, נכתוב פונקציית עזר:
(function [m,p] = findSmallest (v,k
הפונקציה מוצאת את המקום p ואת הערך m הנמצא במערך v והמינימלי מהמקום ה־k־י והלאה %
;p=k
;(m=v(k
;(n=length(v
for i=k+1:n
if v(i)<m
;p=i
;(m=v(i
end
end
end
כעת, נכתוב את התוכנית למיון:
for i=1:n-1 ;(m,p]=findSmallest(v,i] ;(v(p)=v(i ;v(i)=m end
יעילות
אם אנו חושדים שזמן הריצה 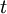 כתלות ב־
כתלות ב־ פרופורציוני ל־
פרופורציוני ל־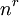 :
:
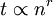
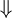
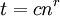
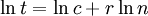
לכן 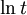 כתלות ב־
כתלות ב־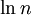 הינו קו ישר ששיפועו
הינו קו ישר ששיפועו 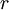 , וכך ניתן למצוא את
, וכך ניתן למצוא את 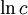 כחיתוך עם ציר y.
כחיתוך עם ציר y.
מספר הגדרות ודוגמות
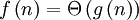 אם
אם 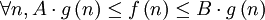 .
.
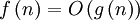 אם
אם 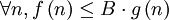 .
.
דוגמה:
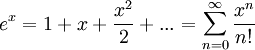 , לכן
, לכן 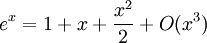 .
.
באופן מדויק: 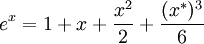 כאשר
כאשר 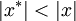 , ולכן
, ולכן 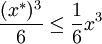 .
.
דוגמה נוספת:
בחיפוש בינארי מבוצעות 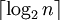 פעולות, ולכן היעילות הינה
פעולות, ולכן היעילות הינה 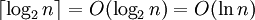 .
.
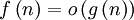 אם
אם 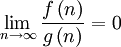 .
.
דוגמה:
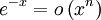 כי
כי 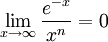
דוגמה נוספת:
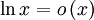 וגם
וגם 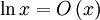 .
.
רקורסיה
מתוך פונקציה שאנו מגדירים ניתן לקרוא לעצמה.
ברקורסיה חשוב לזכור:
- תנאי עצירה
- "צעד" הרקורסיה - זימון הפעולה בתוך עצמה
תרגיל 1 - חישוב עצרת
נזכור כי:
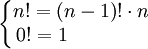
ונכתוב פונקציה מתאימה:
(function [f] = fact (n if n==0 ;f=1 else ;(f=n*fact(n-1 end end
תרגיל 2 - מקדמים בינומיים
המקדם הבינומי  מונה כמה אפשרויות יש לנו לבחירת
מונה כמה אפשרויות יש לנו לבחירת  איברים מתוך
איברים מתוך  ללא בחירת איבר פעמיים וללא חשיבות לסדר.
ללא בחירת איבר פעמיים וללא חשיבות לסדר.
נוסחה סגורה לחישוב: 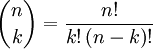
ממשולש פסקל אנו מקבלים נוסחת נסיגה לחישובם: 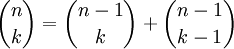 .
.
נכתוב פונקציה מתאימה:
(function [b] = binomial (n,k if k==0 || k==n ;b=1 else ;(b=binomial(n-1,k)+binomial(n-1,k-1 end end
תרגיל 3 - איחוד מערכים ממוינים
המטרה: לאחד שני מערכים ממוינים u,v למערך ממוין
הפונקציה המתאימה:
(function [w] = merge (u,v
;(nu=length(u
;(nv=length(v
;nw=nu+nv
;(w=zeros(nw,1
if nu==0
;w=v
elseif nv==0
;w=u
else
;ku=1
;kv=1
for kw=1:nw
((if (ku<=nu) && (kv>nv || u(ku)<v(kv
;(w(kw)=u(ku
;ku=ku+1
else
;(w(kw)=v(kv
;kv=kv+1
end
end
end
end
תרגיל 4 - מיון מערך
המטרה: למיין מערך ביעילות 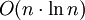
הביצוע: כל פעם נחלק לשני תת־מערכים, נמיין אותם ונאחד (באמצעות הפעולה מתרגיל 3)
הפונקציה המתאימה:
(function [w] = mergeSort (v ;(n=length(v if n<=1 ;w=v else ;(m=floor(n/2 ;((w1=mergeSort(v(1:m ;((w2=mergeSort(v(m+1:n ;(w=merge(w1,w2 end end
משוואות לינאריות
תהי מערכת משוואות 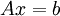 כאשר
כאשר 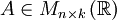 ,
, 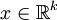 ו־
ו־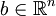 . אזי:
. אזי:
- למערכת אין פתרון אם
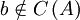 .
. - למערכת יש פתרון יחיד אם
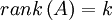 , כלומר
, כלומר 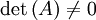 .
. - למערכת יש אינסוף פתרונות אם
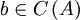 .
.
במקרים 1 ו־3 מתקיים 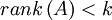 ,
, 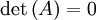 .
.
הערה: 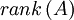 - מספר העמודות הבת"ל ב־
- מספר העמודות הבת"ל ב־ .
.
מקרה 2: פתרון יחיד
שלוש אפשרויות לחישוב הפתרון על ידי MATLAB:
- x=inv(A)*b
- x=A\b
- x=pinv(A)*b
אפשרויות 2 ו־3 מתאימה גם אם  אינה הפיכה / ריבועית.
אינה הפיכה / ריבועית.
מקרה 1: אין פתרון
התאמת קו ישר לאוסף נקודות
עבור סדרת N נקודות, 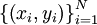 , ננסה להתאים ישר
, ננסה להתאים ישר 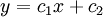 הקרוב להן ביותר (קו מגמה).
הקרוב להן ביותר (קו מגמה).
נגדיר מטריצה  :
:
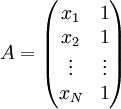
ו־וקטור  :
:
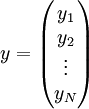
ונפתור את מערכת המשוואות 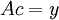 . הפתרון
. הפתרון 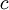 שנקבל הינו הווקטור
שנקבל הינו הווקטור 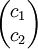
פתרון המערכת: ניעזר ברגרסיה לינארית
נגדיר פונקציה 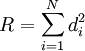 כאשר
כאשר 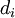 הינו המרחק של הנקודה ה־i־ית מהישר (אנך לציר x), שהוא בעצם הפרשי ה־y. כלומר,
הינו המרחק של הנקודה ה־i־ית מהישר (אנך לציר x), שהוא בעצם הפרשי ה־y. כלומר, 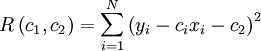 . המינימום של הפונקציה הזו ייתן לנו את הפתרון המקורב ביותר לנקודות, כזה שסכום ריבועי המרחקים שלו מהנקודות הנתונות מינימלי - הכי קרוב.
. המינימום של הפונקציה הזו ייתן לנו את הפתרון המקורב ביותר לנקודות, כזה שסכום ריבועי המרחקים שלו מהנקודות הנתונות מינימלי - הכי קרוב.
נגזור ונקבל נגזרות חלקיות:
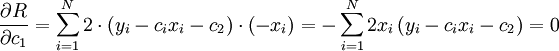
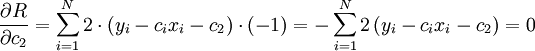
נמשיך לפתור:
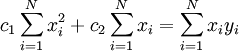
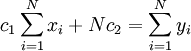
בעצם, קיבלנו מערכת משוואות השקולה למערכת 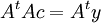 (למי שאינו מאמין, ניתן לבדוק).
(למי שאינו מאמין, ניתן לבדוק).
נחשב את 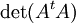 כדי לדעת מתי אין פתרון יחיד למערכת:
כדי לדעת מתי אין פתרון יחיד למערכת:
![\det\left ( A^t A \right )=N\sum_{i=1}^{N}x_i^2-\left ( \sum_{i=1}^{N}x_i \right )^2=N^2 \left [ \frac{\sum_{i=1}^{N}x_i^2}{N}-\left ( \frac{\sum_{i=1}^{N}x_i}{N} \right )^2 \right ]](/images/math/f/5/6/f5690af09a7f2d2420290122fe6513b7.png)
למה: 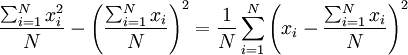
הוכחה: נסמן את הממוצע 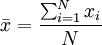 . אזי:
. אזי:
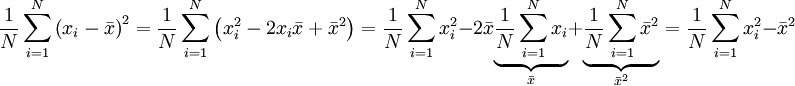
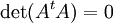 אם ורק אם
אם ורק אם 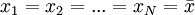 . לכן, קיים פתרון ריבועים מינימליים (Least squares solution).
. לכן, קיים פתרון ריבועים מינימליים (Least squares solution).