תקציר תורת הגרפים, סמסטר א תשע״ג
מתוך Math-Wiki
בתקציר זה, אלא אם צוין אחרת, נסמן ![[n]:=\{1,2,\dots,n\}](/images/math/c/9/4/c949f738b9e523559d2b78c75bbe0126.png) .
.  גרפים.
גרפים.  הוא זוג לא סדור (אלא אם מדובר בגרפים לא מכוונים) ומכפלה קרטזית
הוא זוג לא סדור (אלא אם מדובר בגרפים לא מכוונים) ומכפלה קרטזית 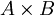 של קבוצות היא קבוצת הזוגות הלא סדורים של איברי
של קבוצות היא קבוצת הזוגות הלא סדורים של איברי 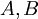 .
.
הגדרות
- גרף הוא זוג
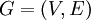 כך ש־
כך ש־ קבוצת קודקודים (נקראים גם "צמתים") ו־
קבוצת קודקודים (נקראים גם "צמתים") ו־ רב קבוצה של זוגות לא סדורים של קודקודים (הזוגות נקראים "צלעות" או "קשתות").
רב קבוצה של זוגות לא סדורים של קודקודים (הזוגות נקראים "צלעות" או "קשתות"). - לולאה היא צלע
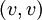 כאשר
כאשר 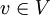 .
. - גרף פשוט הוא גרף ללא לולאות וללא ריבוי צלעות (כלומר, אף צלע לא מופיע פעמיים ב־
 ).
). - גרף מכוון הוא גרף בו הצלעות הן זוגות סדורים.
- אי־הכוונה של גרף מכוון היא הפיכתו לגרף לא מכוון ע״י הפיכת צלעותיו לזוגות לא סדורים.
- הכוונה של גרף לא מכוון היא הפיכתו לגרף מכוון. תיתכן יותר מהכוונה אפשרית אחת.
- הכוונה מעגלית היא הכוונה שבה יש מעגל מכוון.
- גרף סופי הוא גרף בו
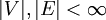 .
. - סדר של גרף הוא מספר הקודקודים בו, כלומר
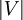 . לעתים מסומן
. לעתים מסומן 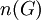 .
. - מידה של גרף היא מספר הצלעות –
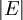 . לעתים מסומנת
. לעתים מסומנת 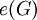 או
או 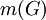 .
. - דרגה של קודקוד
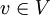 היא מספר הצלעות העוברות בו. מסומנת
היא מספר הצלעות העוברות בו. מסומנת 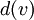 או
או 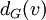 .
.
- הדרגה המקסימלית:
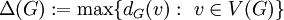 .
. - הדרגה המינימלית:
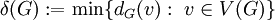 .
. - דרגות החוץ והפנים של קודקוד בגרף מכוון הן
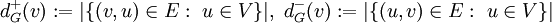 בהתאמה, כלומר מספר הצלעות היוצאות ומספר הצלעות הנכנסות לקודקוד בהתאמה.
בהתאמה, כלומר מספר הצלעות היוצאות ומספר הצלעות הנכנסות לקודקוד בהתאמה.
- הדרגה המקסימלית:
- איחוד של גרפים פשוטים
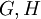 הוא
הוא 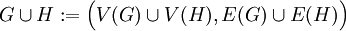 . באותו אופן מוגדר איחוד זר.
. באותו אופן מוגדר איחוד זר. - קבוצת השכנים של קודקוד
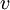 בגרף
בגרף  היא
היא 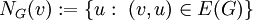 . אם
. אם 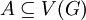 אז
אז 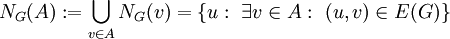 .
.
סוגי גרפים נפוצים
- גרף ריק
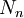 הוא הגרף שסדרו
הוא הגרף שסדרו  ומידתו 0.
ומידתו 0. - גרף מלא/שלם
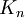 הוא הגרף שסדרו
הוא הגרף שסדרו  ובין כל שני קודקודים יש צלע אחת בדיוק.
ובין כל שני קודקודים יש צלע אחת בדיוק.
- קליקה בגרף היא תת־גרף מלא.
- מספר הקליקה של גרף
 מסומן
מסומן 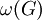 ושווה לסדר המקסימלי של קליקה ב־
ושווה לסדר המקסימלי של קליקה ב־ .
.
- מסילה
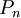 היא הגרף שסדרו
היא הגרף שסדרו  ושניתן לסדר את קודקודיו כ־
ושניתן לסדר את קודקודיו כ־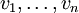 ואז
ואז 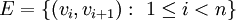 .
. - מעגל
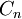 (
(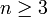 ) הוא הגרף שסדרו
) הוא הגרף שסדרו  ושניתן לסדר את קודקודיו כ־
ושניתן לסדר את קודקודיו כ־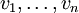 ואז
ואז 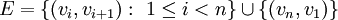 .
.
- מותן (girth) של גרף
 הוא אורך המעגל הקטן ביותר בגרף, ומסומן
הוא אורך המעגל הקטן ביותר בגרף, ומסומן 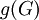 . אם אין בגרף מעגלים (יער) אז
. אם אין בגרף מעגלים (יער) אז 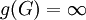 .
.
- מותן (girth) של גרף
- גרף d־רגולרי הוא גרף שבו דרגת כל קודקוד היא
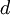 .
.
- גרף d+־רגולרי הוא גרף מכוון שבו דרגת החוץ של כל קודקוד היא
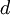 . באותו אופן מגדירים גרף
. באותו אופן מגדירים גרף 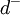 ־רגולרי.
־רגולרי.
- גרף d+־רגולרי הוא גרף מכוון שבו דרגת החוץ של כל קודקוד היא
- גרף דו־צדדי (דו״צ) הוא גרף פשוט
 שבו קיימת חלוקה
שבו קיימת חלוקה 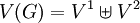 כך ש־
כך ש־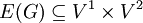 .
.
- גרף דו־צדדי מלא
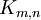 הוא הגרף שקודקודיו הם
הוא הגרף שקודקודיו הם 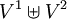 (כאשר
(כאשר 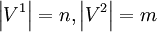 ) וצלעותיו
) וצלעותיו 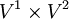 .
. - גרף r־צדדי הוא גרף
 בו יש חלוקה
בו יש חלוקה 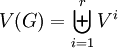 ל־
ל־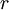 תתי־קבוצות כך שלכל
תתי־קבוצות כך שלכל 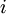 הקודקודים ב־
הקודקודים ב־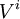 אינם שכנים, כלומר
אינם שכנים, כלומר 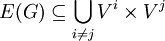 .
. - גרף r־צדדי מלא הוא גרף
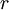 ־צדדי
־צדדי  בו
בו 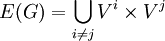 , כלומר שני קודקודים הם שכנים אם״ם הם נמצאים בצדדים שונים.
, כלומר שני קודקודים הם שכנים אם״ם הם נמצאים בצדדים שונים. - גרף r־צדדי סימטרי הוא גרף
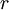 ־צדדי בו
־צדדי בו ![\forall i\in[r]:\ \left|V^i\right|\in\left\{\left\lfloor\frac{|V(G)|}r\right\rfloor,\left\lceil\frac{|V(G)|}r\right\rceil\right\}](/images/math/b/0/1/b01f5acb8288083d3e489e1b18e79127.png) .
. - גרף טורן
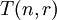 הוא הגרף ה־
הוא הגרף ה־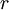 ־צדדי סימטרי מלא מסדר
־צדדי סימטרי מלא מסדר  .
.
- גרף דו־צדדי מלא
- גרף מסומן הוא גרף שקודקודיו סומנו ע״י
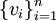 . שני גרפים מסומנים הם זהים אם״ם קיים איזומורפיזם
. שני גרפים מסומנים הם זהים אם״ם קיים איזומורפיזם 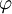 בינהם כך ש־
בינהם כך ש־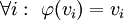 .
.
עצים
- יער הוא גרף פשוט ללא מעגלים.
- עץ הוא יער קשיר.
- עלה הוא קודקוד בעץ שדרגתו 1.
- עץ פורש הוא תת־גרף פורש קשיר ללא מעגלים.
הילוכים
- הילוך בגרף הוא סדרת קודקודים (חזרות מותרות) כך שכל קודקוד שכן של הסמוכים לו. כלומר, זו סדרה
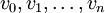 כך ש־
כך ש־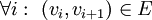 .
.
- אורך ההילוך הוא
 – מספר הצלעות שבו, כלומר מספר הקודקודים פחות 1.
– מספר הצלעות שבו, כלומר מספר הקודקודים פחות 1. - ההילוך סגור אם
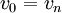 .
.
- אורך ההילוך הוא
- המרחק בין שני קודקודים
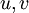 הוא המרחק המינימלי של הילוך בינהם (אם יש כזה) ומסומן
הוא המרחק המינימלי של הילוך בינהם (אם יש כזה) ומסומן 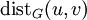 .
. - הקוטר של גרף הוא
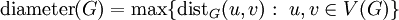 .
. - מסלול הוא הילוך שבו אין צלעות חוזרות.
- מסילה היא הילוך שבו אין קודקודים חוזרים, למעט אם הקודקוד הראשון שווה לקודקוד האחרון.
- רכיב קשירות בגרף לא מכוון הוא מחלקת שקילות של יחס השקילות
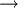 המקיים
המקיים 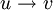 אם״ם יש מסילה בין
אם״ם יש מסילה בין 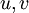 .
. - מספר רכיבי הקשירות בגרף
 יסומן
יסומן 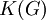 .
. - גרף קשיר הוא גרף שבו יש רכיב קשירות אחד.
- מסלול אוילר בגרף ללא לולאות הוא מסלול המכיל את כל צלעות הגרף.
- אוילריאן הוא גרף בו קיים מסלול אוילר סגור.
- סמי־אוילריאן הוא גרף בו קיים מסלול אוילר.
- מסילה המילטוניאנית בגרף היא מסילה המכילה את כל קודקודיו.
- מעגל המילטוניאני הוא מסילה המילטוניאנית סגורה.
- המילטוניאן הוא גרף בו קיים מעגל המילטוניאני.
- הילוך אקראי: יהי
 גרף לא מכוון וסופי. במצב ההתחלתי
גרף לא מכוון וסופי. במצב ההתחלתי 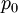 נמצאים על הקודקוד
נמצאים על הקודקוד 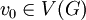 בהסתברות 1, ובכל צעד פונים לשכן של הקודקוד הנוכחי כאשר לכל שכן הסתברות שווה. ההילוך שנוצר מקודקודים אלו נקרא הילוך אקראי.
בהסתברות 1, ובכל צעד פונים לשכן של הקודקוד הנוכחי כאשר לכל שכן הסתברות שווה. ההילוך שנוצר מקודקודים אלו נקרא הילוך אקראי. - הסתברות החזרה בזמן
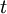 היא ההסתברות שלאחר
היא ההסתברות שלאחר 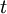 צעדים נהיה על הקודקוד בו התחלנו, ומסומנת
צעדים נהיה על הקודקוד בו התחלנו, ומסומנת 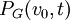 כאשר
כאשר 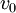 הקודקוד ההתחלתי.
הקודקוד ההתחלתי. - הסתברות החזרה הממוצעת בזמן
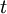 היא
היא 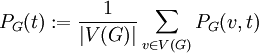 .
.
איזומורפיזם
- איזומורפיזם בין מגרף
 לגרף
לגרף 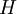 הוא פונקציה
הוא פונקציה 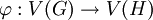 חח״ע ועל ששומרת צלעות, כלומר
חח״ע ועל ששומרת צלעות, כלומר 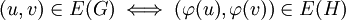 לכל
לכל 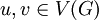 . אם קיים איזומורפיזם בין
. אם קיים איזומורפיזם בין 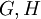 אז נאמר שהם איזומורפיים ונסמן
אז נאמר שהם איזומורפיים ונסמן 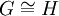 (זה יחס שקילות).
(זה יחס שקילות). - גרף טרנזיטיבי קודקודים הוא גרף
 בו לכל
בו לכל 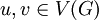 קיים אוטומורפיזם
קיים אוטומורפיזם 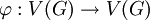 כך ש־
כך ש־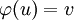 .
.
גרפים הנוצרים מגרפים אחרים
תת־גרף
- השמטת צלע
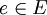 מגרף
מגרף  היא הפיכת הגרף ל־
היא הפיכת הגרף ל־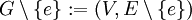 .
. - השמטת קודקוד
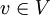 מגרף
מגרף  היא הפיכת הגרף ל־
היא הפיכת הגרף ל־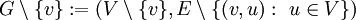 .
. - תת־גרף הוא הגרף המתקבל מסדרה של השמטות קודקודים ו/או צלעות.
- תת־גרף פורש הוא תת־גרף המתקבל מסדרה של השמטות צלעות בלבד.
- תת־גרף מושרה הוא תת־גרף המתקבל מסדרה של השמטות קודקודים בלבד.
חלוקה
- חלוקה אלמנטרית של צלע
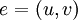 בגרף
בגרף  היא
היא 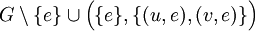 .
. - חלוקה של גרף היא היא גרף המתקבל מסדרה של חלוקות אלמנטריות.
כיווץ
- כיווץ של גרף
 בצלע
בצלע 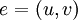 הוא
הוא 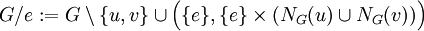 .
. - מינור של גרף פשוט הוא גרף המתקבל ממנו ע״י סדרה של השמטות קודקודים, השמטות צלעות וכיווצי צלעות.
- תכונה מונוטונית של גרף היא תכונה הסגורה תחת מינור, כלומר אם גרף מקיים אותה אז כל מינור שלו מקיים אותה.
גרף משלים
- הגרף המשלים של גרף
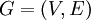 הוא
הוא 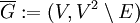 .
.
גרף הקו
- גרף הקו של גרף פשוט
 מסומן
מסומן 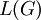 ומוגדר כגרף שקודקודיו הם
ומוגדר כגרף שקודקודיו הם 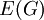 וצלעותיו הם זוגות של צלעות שיש להן קודקוד משותף ב־
וצלעותיו הם זוגות של צלעות שיש להן קודקוד משותף ב־ , כלומר
, כלומר 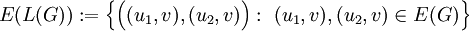 .
.
מכפלה קרטזית של גרפים
- המכפלה הקרטזית של הגרפים
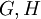 היא גרף המסומן כ־
היא גרף המסומן כ־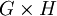 . קודקודיו הם
. קודקודיו הם 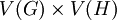 (כשהקודקודים הם זוגות סדורים) וצלעותיו
(כשהקודקודים הם זוגות סדורים) וצלעותיו 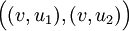 כאשר
כאשר 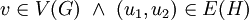 או
או 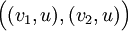 כאשר
כאשר 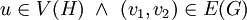 .
. - קובייה n־מימדית היא
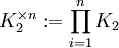 .
.
שיכון
- שיכון של גרף
 ב־
ב־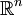 הוא העתקה חח״ע
הוא העתקה חח״ע 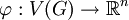 . כל צלע
. כל צלע 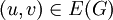 מועתקת למסילה רציפה ופשוטה (כלומר, שאינה חותכת את עצמה) מ־
מועתקת למסילה רציפה ופשוטה (כלומר, שאינה חותכת את עצמה) מ־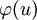 ל־
ל־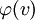 .
. - שיכון נאות הוא שיכון אם אין חיתוך צלעות לא טריוויאלי, כלומר התמונות של הצלעות ב־
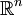 חותכות זו את זו רק בתמונות של קודקודי הגרף.
חותכות זו את זו רק בתמונות של קודקודי הגרף. - גרף מישורי הוא גרף שניתן לשיכון נאות ב־
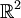 .
. - פאה של שיכון נאות ב־
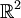 היא רכיב קשירות ב־
היא רכיב קשירות ב־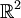 לאחר שהוציאו ממנו את התמונה של השיכון.
לאחר שהוציאו ממנו את התמונה של השיכון. - גרף חוץ־מישורי הוא גרף שניתן לשכן באופן נאות במישור כך שקודקודיו על מעגל וצלעותיו קטעים ישרים.
גופים אפלטוניים
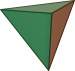
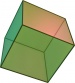
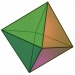
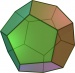
- גוף אפלטוני הוא פאון תלת־מימדי שכל פאותיו מצולעים משוכללים חופפים. הגופים האפלטונים הם הטטרהדרון (
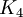 ), ההקסהדרון (קובייה,
), ההקסהדרון (קובייה, 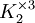 ), האוקטהדרון (
), האוקטהדרון (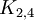 ), הדודקהדרון והאיקוסהדרון.
), הדודקהדרון והאיקוסהדרון. - פאון דואלי של גוף אפלטוני הוא הפאון המתקבל לאחר שלכל פאה בגוף האפלטוני שמים קודקוד במרכז ומחברים צלעות בין קודקודים של פאות להן צלע משותפת.
צביעה
- k־צביעת קודקודים או k־צביעה בגרף
 ללא לולאות היא פונקציה
ללא לולאות היא פונקציה ![f:V(G)\to[k]](/images/math/e/a/b/eab1759eb741794690c1108f8b83f0ac.png) .
. - k־צביעה כשרה היא
 ־צביעה
־צביעה  שבה לכל צלע
שבה לכל צלע 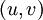 מתקיים
מתקיים 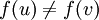 . כלומר, קודקודים שכנים צבועים בצבעים שונים.
. כלומר, קודקודים שכנים צבועים בצבעים שונים. - מספר הצביעה או המספר הכרומטי של גרף
 מסומן כ־
מסומן כ־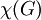 ומוגדר כ־
ומוגדר כ־ המינימלי עבורו קיימת
המינימלי עבורו קיימת  ־צביעה כשרה.
־צביעה כשרה. - גרף k־צביע הוא גרף שקיימת לו
 ־צביעה כשרה, כלומר
־צביעה כשרה, כלומר 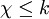 .
. - פולינום הצביעה בגרף פשוט וסופי מסומן
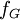 . לכל
. לכל  טבעי
טבעי 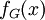 מוגדר כמספר ה־
מוגדר כמספר ה־ ־צביעות הכשרות. לשאר ה־
־צביעות הכשרות. לשאר ה־ ־ים
־ים 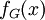 הוא ההשלמה של
הוא ההשלמה של 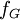 לפולינום.
לפולינום. - k־צביעת צלעות בגרף
 היא פונקציה
היא פונקציה ![f:E(G)\to[k]](/images/math/7/8/c/78ccad804542cf851e26fba5d6956d93.png) .
. - k־צביעת צלעות כשרה היא
 ־צביעת צלעות בה אם לשתי צלעות יש קודקוד משותף אז הן צבועות בצבעים שונים.
־צביעת צלעות בה אם לשתי צלעות יש קודקוד משותף אז הן צבועות בצבעים שונים. - אינדקס הצביעה
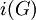 של גרף
של גרף  הוא ה־
הוא ה־ המינימלי עבורו קיימת
המינימלי עבורו קיימת  ־צביעת צלעות כשרה.
־צביעת צלעות כשרה.
שידוך
- שידוך בגרף
 הוא התאמה חח״ע ועל
הוא התאמה חח״ע ועל 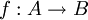 כאשר
כאשר 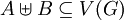 ו־
ו־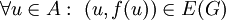 .
. - שידוך מושלם
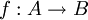 הוא שידוך בו
הוא שידוך בו 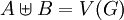 .
. - שידוך מלא מ־
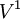 ל־
ל־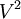 בגרף
בגרף  דו־צדדי ש־
דו־צדדי ש־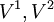 הם צדדיו הינו התאמה חח״ע (לאו דווקא על)
הם צדדיו הינו התאמה חח״ע (לאו דווקא על) 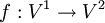 כך ש־
כך ש־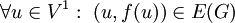 .
.
אי־תלות
- קבוצה בלתי־תלויה של צלעות בגרף
 היא תת־קבוצה של
היא תת־קבוצה של 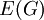 שבה אין שתי צלעות בעלות קודקוד משותף.
שבה אין שתי צלעות בעלות קודקוד משותף. - קבוצה בלתי־תלויה של קודקודים בגרף
 היא תת־קבוצה של
היא תת־קבוצה של 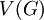 שמשרה גרף ריק, כלומר שבה אין שני קודקודים שכנים.
שמשרה גרף ריק, כלומר שבה אין שני קודקודים שכנים. -
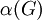 הוא הגודל המקסימלי של קבוצה בלתי־תלויה של קודקודים ב־
הוא הגודל המקסימלי של קבוצה בלתי־תלויה של קודקודים ב־ .
.
בעיות קיצון
- בעיית טורן: בהנתן גרף
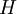 (או קבוצת גרפים
(או קבוצת גרפים 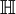 ) ומספר טבעי
) ומספר טבעי  יש למצוא את המידה המקסימלית האפשרית בגרף פשוט מסדר
יש למצוא את המידה המקסימלית האפשרית בגרף פשוט מסדר  שאין לו תת־גרף איזומורפי ל־
שאין לו תת־גרף איזומורפי ל־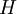 (או לאחד מהגרפים ב־
(או לאחד מהגרפים ב־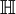 ). מספר זה מסומן כ־
). מספר זה מסומן כ־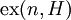 או
או 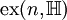 וגרף כזה נקרא גרף מרבי נמנע
וגרף כזה נקרא גרף מרבי נמנע 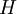 (או
(או 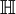 ).
). - מספר רמזי
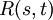 הוא הסדר המינימלי כך שאם
הוא הסדר המינימלי כך שאם  גרף מסדר זה אז
גרף מסדר זה אז 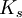 תת־גרף של
תת־גרף של  או ש־
או ש־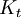 תת־גרף של
תת־גרף של 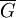 .
.
תורת הגרפים האלגברית
- מטריצת השכנות של גרף סופי
 (מכוון או לא) כך ש־
(מכוון או לא) כך ש־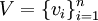 היא
היא 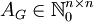 שבה
שבה 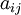 הוא מספר הצלעות מ־
הוא מספר הצלעות מ־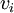 ל־
ל־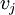 .
. - נסמן
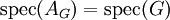 כרב־קבוצה של הע״ע של
כרב־קבוצה של הע״ע של 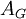 (כאשר כל ע״ע מופיע בריבוי השווה לריבוי האלגברי שלו).
(כאשר כל ע״ע מופיע בריבוי השווה לריבוי האלגברי שלו). - מטריצת הדרגות של גרף
 מסדר
מסדר  שקודקודיו
שקודקודיו 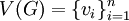 היא המטריצה
היא המטריצה 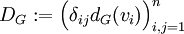 .
. - הלפלסיאן של
 הוא
הוא 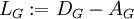 .
.
משפטים
-
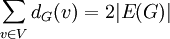 .
. -
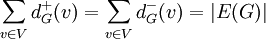 .
. - אם
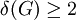 אז יש ב־
אז יש ב־ מעגל.
מעגל. -
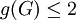 אם״ם הגרף לא פשוט.
אם״ם הגרף לא פשוט. - גרף הוא ריק אם״ם הוא 0־רגולרי.
- גרף 1־רגולרי ופשוט הוא איחוד זר של צלעות.
- גרף 2־רגולרי ופשוט הוא איחוד זר של מעגלים.
- אם גרף סופי ופשוט הוא
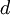 ־רגולרי כך ש־
־רגולרי כך ש־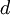 אי־זוגי אזי הגרף מסדר זוגי.
אי־זוגי אזי הגרף מסדר זוגי. - גרף פשוט הוא עץ אם״ם בין כל שני קודקודים יש מסילה יחידה.
- בכל עץ סופי מסדר גדול מ־1 יש עלה.
- גרף הוא עץ אם״ם הוא קשיר מינימלי, כלומר הוא קשיר וכל השמטת צלע יוצרת תת־גרף לא קשיר.
- גרף הוא עץ אם״ם הוא מקסימלי ללא מעגלים, כלומר הוא עץ וכל הוספת צלע יוצרת מעגל.
- לכל גרף קשיר וסופי קיים עץ פורש.
- משפט קיילי: יש
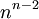 עצים מסומנים מסדר
עצים מסומנים מסדר  .
. - משפט מטריצה–עץ/משפט עצים פורשים: כידוע, מינור
![A[i,j]](/images/math/2/4/e/24edb2ea71428b08548c56890a88df9b.png) של מטריצה
של מטריצה  הוא המטריצה המתקבלת מהשמטת השורה ה־
הוא המטריצה המתקבלת מהשמטת השורה ה־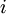 והעמודה ה־
והעמודה ה־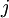 . נסמן
. נסמן 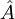 כמינור המוחק את השורה והעמודה האחרונות. עתה יהי
כמינור המוחק את השורה והעמודה האחרונות. עתה יהי  גרף לא מכוון וסופי מסדר הגדול מ־1. מספר העצים הפורשים שלו שווה ל־
גרף לא מכוון וסופי מסדר הגדול מ־1. מספר העצים הפורשים שלו שווה ל־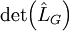 .
. - בעיית הסוכן הנוסע: נתו גרף קשיר וסופי ורוצים למצוא את ההילוך הקצר ביותר העובר דרך כל קודקודי הגרף. הפתרון הכי יעיל לא ידוע, אבל יש פתרון הנותן הילוך שאורכו לכל היותר פי 2 מהפתרון המינימלי: מוצאים עץ פורש לגרף ומבצעים עליו חיפוש DFS.
- ביער מסדר
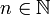 עם
עם  רכיבי קשירות יש
רכיבי קשירות יש 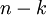 צלעות.
צלעות. - גרף הוא יער אם״ם אין לו מינור שאיזומורפי ל־
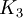 .
. - כל מסילה היא מסלול.
- קיים הילוך בין שני קודקודים אם״ם קיימת מסילה בינהם.
- גרף הוא קשיר אם״ם הוא אינו איחוד זר של שני גרפים.
- משפט אוילר: גרף קשיר וסופי ללא לולאות הוא אוילריאן אם״ם דרגות כל הקודקודים זוגיות.
- גרף
 קשיר וסופי ללא לולאות הוא סמי־אוילריאן שאינו אוילריאן אם״ם דרגות כל הקודקודים זוגיות פרט לשני קודקודים.
קשיר וסופי ללא לולאות הוא סמי־אוילריאן שאינו אוילריאן אם״ם דרגות כל הקודקודים זוגיות פרט לשני קודקודים. - משפט דיראק: יהי
 גרף פשוט מסדר
גרף פשוט מסדר  . אם
. אם 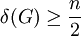 אז
אז  המילטוניאן.
המילטוניאן. - אם
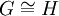 אז הפרמטרים הבאים שווים:
אז הפרמטרים הבאים שווים:
- סדר:
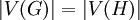 .
. - מידה:
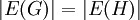 .
. - מספר רכיבי הקשירות:
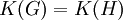 .
. - וקטור דרגות (וקטור דרגות של גרף הוא וקטור שרכיביו הם דרגות הקודקודים מסודרות בסדר יורד חלש).
- קוטר:
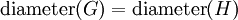 .
.
- סדר:
-
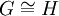 אם״ם
אם״ם 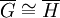 .
. -
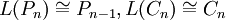 .
. - הקובייה ה־
 מימדית
מימדית 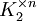 איזומורפית ל־
איזומורפית ל־![B_n:=(\mathcal P([n]),\{(I,J):\ I\subset J\subseteq[n]\ \and\ |I|=|J|-1\})](/images/math/7/1/7/717404881e128a759b193f59e049b966.png) ול־
ול־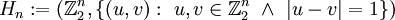 .
. - לכל גרף עם מספר בן מנייה של קודקודים קיים שיכון נאות ב־
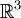 כך שהתמונות של הצלעות הן קטעים ישרים. אם הגרף הוא סופי ופשוט אז שיכון נאות מתאים הוא, לדוגמה,
כך שהתמונות של הצלעות הן קטעים ישרים. אם הגרף הוא סופי ופשוט אז שיכון נאות מתאים הוא, לדוגמה, 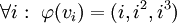 כאשר
כאשר 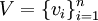 .
. - משפט הפאון של אוילר: לכל גרף מישורי סופי קשיר מסדר
 וממידה
וממידה 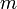 מספר הפאות
מספר הפאות  לא תלוי בשיכון הנאות ומקיים
לא תלוי בשיכון הנאות ומקיים 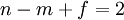 .
. - יהי
 גרף פשוט וקשיר מסדר
גרף פשוט וקשיר מסדר 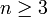 . אם
. אם  מישורי אז
מישורי אז 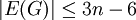 .
. - יהי
 פשוט וקשיר מסדר
פשוט וקשיר מסדר  ומותן
ומותן 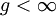 . אם
. אם  מישורי אז
מישורי אז 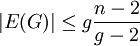 .
. - לכל גרף מישורי פשוט סופי
 מתקיים
מתקיים 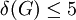 .
. - משפט קורטובסקי: גרף אינו מישורי אם״ם יש לו תת־גרף שאיזומורפי לחלוקה של
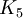 או של
או של 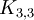 .
. - גרף הוא חוץ־מישורי אם״ם אין לו מינור שאיזומורפי ל־
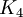 או ל־
או ל־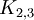 .
. - השערת וגנר: כל תכונה היא מונוטונית אם״ם היא מוגדרת ע״י קבוצה סופית של מינורים אסורים, כלומר קיים מספר סופי של גרפים שאיזומורפים למינור כלשהו של
 אם״ם הוא אינו מקיים את התכונה.
אם״ם הוא אינו מקיים את התכונה. - משפט רוברטסון–סימור: השערת וגנר נכונה.
- הגרף של כל גוף אפלטוני הוא מישורי.
- לכל גרף
 פשוט
פשוט 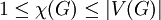 .
. 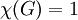 אם״ם
אם״ם  גרף ריק ו־
גרף ריק ו־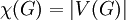 אם״ם הוא גרף מלא.
אם״ם הוא גרף מלא. - משפט ברוקס: לכל גרף
 פשוט וסופי
פשוט וסופי 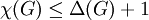 ושוויון מתקיים אם״ם
ושוויון מתקיים אם״ם 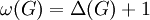 או אם
או אם  איחוד זר של מעגלים ומסילות ויש מעגל מסדר אי־זוגי.
איחוד זר של מעגלים ומסילות ויש מעגל מסדר אי־זוגי. - יהא
 פשוט וסופי.
פשוט וסופי. 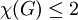 אם״ם אין ב־
אם״ם אין ב־ מעגלים מאורך אי־זוגי.
מעגלים מאורך אי־זוגי. - גרף הוא 2־צביע אם״ם הוא דו־צדדי.
- בעיית 4 הצבעים: לכל גרף מישורי סופי פשוט
 הוא 4־צביע.
הוא 4־צביע. -
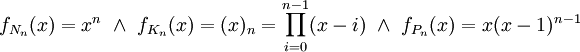 .
. -
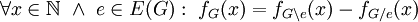 .
. -
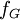 פולינום מתוקן ודרגתו
פולינום מתוקן ודרגתו 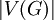 .
. -
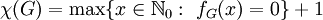 .
. - משפט סטנלי: מספר ההכוונות הלא מעגליות של
 הוא
הוא 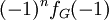 .
. - לכל גרף
 סופי
סופי 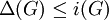 . אם הוא לא ריק אז
. אם הוא לא ריק אז 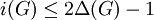 .
. - אם
 דו־צדדי ו־
דו־צדדי ו־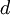 ־רגולרי אז
־רגולרי אז 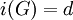 .
. - אם
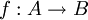 שידוך אז
שידוך אז 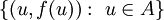 קבוצה בלתי־תלויה.
קבוצה בלתי־תלויה. - משפט הול (Hall): לכל גרף דו־צדדי שצדדיו
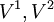 קיים שידוך מלא מ־
קיים שידוך מלא מ־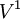 ל־
ל־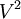 אם״ם
אם״ם 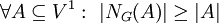 .
. - משפט טורן: הגרף המרבי נמנע
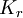 היחיד מסדר
היחיד מסדר  הוא
הוא 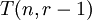 .
. - אם
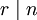 אז
אז 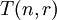 הוא
הוא 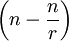 ־רגולרי ו־
־רגולרי ו־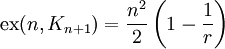 .
. - למת לחיצות הידיים: עבור כל גרף פשוט מסדר 6 או ש־
 מכיל משולש או ש־
מכיל משולש או ש־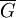 מכיל משולש. (למעשה,
מכיל משולש. (למעשה, 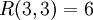 .)
.) -
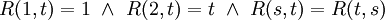 ואם
ואם 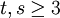 אז
אז 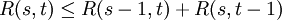 .
. -
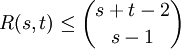 .
. - אם
 לא מכוון אז
לא מכוון אז 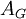 סימטרית.
סימטרית. - לכל גרף סופי מתקיים
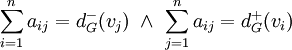 .
. - העקבה
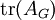 היא מספר הלולאות ב־
היא מספר הלולאות ב־ .
. - יהי
 פשוט ולא מכוון. אזי
פשוט ולא מכוון. אזי 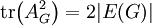 .
. - יהי
 לא מכוון. אזי
לא מכוון. אזי 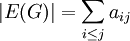 .
. - מספר ההילוכים מ־
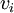 ל־
ל־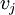 מאורך
מאורך 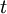 הוא
הוא 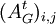 .
. - מספר ההילוכים הסגורים מאורך
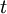 ב־
ב־ הוא
הוא 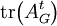 (כאשר שני הילוכים שמתחילים בנקודות שונות הם שונים גם אם הם עוברים על אותן נקודות).
(כאשר שני הילוכים שמתחילים בנקודות שונות הם שונים גם אם הם עוברים על אותן נקודות). - אם
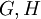 סופיים ולא מכוונים אז
סופיים ולא מכוונים אז 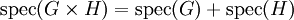 .
. - אם
 גרף
גרף 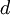 ־רגולרי אז
־רגולרי אז 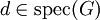 וו״ע מתאימים הם
וו״ע מתאימים הם 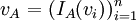 לכל רכיב קשירות
לכל רכיב קשירות 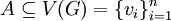 .
. - יהא
 סופי ולא מכוון.
סופי ולא מכוון.  דו־צדדי אם״ם מתקיים התנאי הבא:
דו־צדדי אם״ם מתקיים התנאי הבא:  ע״ע של
ע״ע של 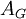 מריבוי אלגברי
מריבוי אלגברי  אם״ם
אם״ם 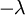 ע״ע מאותו ריבוי.
ע״ע מאותו ריבוי. - הלפלסיאנים של שני גרפים זהים אם״ם יש להם תתי־גרפים פורשים איזומורפיים.
- הלפלסיאן של גרף לא מכוון הוא מטריצה סימטרית.
- הלפלסיאן אינו מטריצה הפיכה.
- אם
 לא מכוון סופי אז
לא מכוון סופי אז 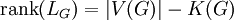 .
. - בגרף טרנזיטיבי קודקודים
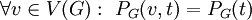 .
. - יהא
 לא מכוון, סופי ו־
לא מכוון, סופי ו־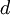 ־רגולרי מסדר
־רגולרי מסדר  . אזי
. אזי 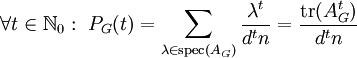 .
.