תרגול 12 תשעז
חזרה לדף מערכי התרגול.
תוכן עניינים
הגדרות בסיסיות לפונקציות
הגדרה: יהיו 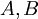 קבוצות ו-
קבוצות ו- יחס בינהן. אזי:
יחס בינהן. אזי:
- התחום של R הינו
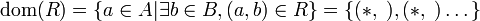
- התמונה של R הינה
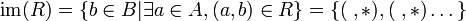
הערה: ישירות מהגדרה מתקיים כי 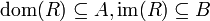 .
.
דוגמה:
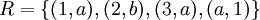 אזי התחום הוא
אזי התחום הוא 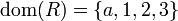 והתמונה הינה
והתמונה הינה 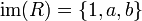 .
.
הגדרה:
- יחס
 מ-
מ- ל-
ל- נקרא על אם
נקרא על אם 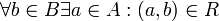 כלומר
כלומר 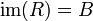 .
. - יחס
 מ-
מ- ל-
ל- נקרא מלא אם
נקרא מלא אם 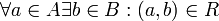 כלומר
כלומר 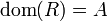
- יחס
 נקרא חד ערכי אם
נקרא חד ערכי אם ![[(x,b)\in R] \and [(x,d) \in R] \rightarrow (d=b)](/images/math/8/b/a/8ba1cf7695007d890739c921bba19ad7.png) כלומר אין איבר מ-
כלומר אין איבר מ- שמתאים לשני איברים שונים מ-
שמתאים לשני איברים שונים מ- .
.
הגדרה:
יחס חד ערכי ומלא נקרא פונקציה; נסמן במקרה זה 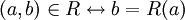 .
ובאופן כללי
.
ובאופן כללי 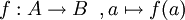 .
(
.
( נקרא תחום (הגדרה) של הפונקציה ו-
נקרא תחום (הגדרה) של הפונקציה ו- נקרא הטווח של הפונקציה.)
נקרא הטווח של הפונקציה.)
פונקציה נקראת חד-חד ערכית אם בנוסף היחס ההפוך הוא חד ערכי.
כלומר:
 חח"ע אמ"מ
חח"ע אמ"מ 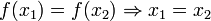 אמ"מ
אמ"מ 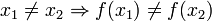 .
.
הגדרה:
תהא  קבוצה. פונקציית הזהות היא פונקציה
קבוצה. פונקציית הזהות היא פונקציה 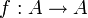 המקיימת
המקיימת 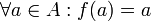 . נהוג לסמנה
. נהוג לסמנה 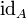 . פונקציית הזהות היא חח"ע ועל.
. פונקציית הזהות היא חח"ע ועל.
דוגמאות
באופן רשלני (וחסכוני), כאשר אנחנו מגדירים פונקציה לא תמיד נשתמש בכמת "לכל" לגבי איברי תחום ההגדרה.
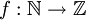 כאשר
כאשר 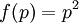 חח"ע ואינה על.
חח"ע ואינה על.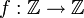 כאשר
כאשר 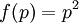 אינה חח"ע ואינה על.
אינה חח"ע ואינה על.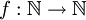 כאשר
כאשר 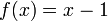 לא מוגדרת כי
לא מוגדרת כי 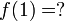 .
.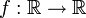 כאשר
כאשר 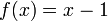 חח"ע ועל.
חח"ע ועל.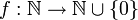 כאשר
כאשר 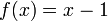 חח"ע ועל.
חח"ע ועל.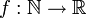 כאשר
כאשר 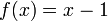 חח"ע ואינה על.
חח"ע ואינה על.- תהא פונקציה
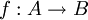 אזי
אזי 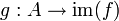 המוגדרת לכל
המוגדרת לכל 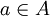 לפי
לפי 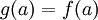 היא על (במילים: פשוט חושבים על הטווח של
היא על (במילים: פשוט חושבים על הטווח של  להיות התמונה של
להיות התמונה של  ).
). - תהא
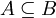 אזי הפונקציה
אזי הפונקציה 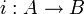 המוגדרת לכל
המוגדרת לכל 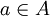 לפי
לפי 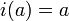 נקראת פונקציה ההכלה (אם
נקראת פונקציה ההכלה (אם 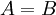 זו פונקצית הזהות). פונקצית ההכלה היא חח"ע.
זו פונקצית הזהות). פונקצית ההכלה היא חח"ע.
תרגיל
תהיינה 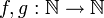 פונקציות כך ש-
פונקציות כך ש-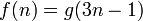 .
.
הוכיחו שאם  על, אז
על, אז  לא חח"ע.
לא חח"ע.
פתרון
נסמן 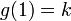 כיון ש-
כיון ש- על אזי קיים
על אזי קיים 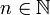 כך ש
כך ש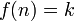 . מהנתון נקבל ש-
. מהנתון נקבל ש-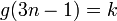 . כעת, כיון ש-
. כעת, כיון ש- 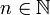 אזי ברור ש-
אזי ברור ש-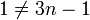 , ולכן אילו שני איברים שונים שנשלחים לאותו איבר. לכן
, ולכן אילו שני איברים שונים שנשלחים לאותו איבר. לכן  לא חח"ע.
לא חח"ע.
תרגיל
נסמן ב-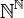 את אוסף הפונקציות מהטבעיים לעצמם.
את אוסף הפונקציות מהטבעיים לעצמם.
נתבונן בפונקציה 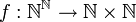 המוגדרת ע"י
המוגדרת ע"י 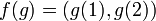 האם היא חח"ע? האם היא על?
האם היא חח"ע? האם היא על?
פתרון
הפונקציה לא חח"ע כי יש הרבה פונקציות שנותנות ל-1,2 (יחד!) את אותם ערכים.
היא כן על: לכל זוג סדור 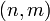 הפונקציה ששולחת את 1 ל-
הפונקציה ששולחת את 1 ל- , ואת 2 ל-
, ואת 2 ל-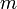 , היא המקור (את שאר הטבעיים נשלח לאן שנרצה).
, היא המקור (את שאר הטבעיים נשלח לאן שנרצה).
תרגיל
יהיו  ו-
ו- קבוצות סופיות בעלות עוצמה זהה. הוכיחו שכל פונקציה מ-
קבוצות סופיות בעלות עוצמה זהה. הוכיחו שכל פונקציה מ- ל-
ל- הינה על אם"ם היא חח"ע.
הינה על אם"ם היא חח"ע.
הוכחה:
נסמן 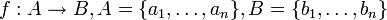 . כאשר כל האיברים ב-
. כאשר כל האיברים ב- שונים זה מזה וכנ"ל ב-
שונים זה מזה וכנ"ל ב- .
.
נניח  חח"ע אזי
חח"ע אזי 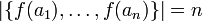 כיוון ש-
כיוון ש-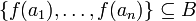 ובשניהם יש אותו מספר איברים, מתקיים שיוון ולכן
ובשניהם יש אותו מספר איברים, מתקיים שיוון ולכן  על.
על.
נניח  על. נניח בשלילה ש-
על. נניח בשלילה ש- אינה חח"ע אזי
אינה חח"ע אזי 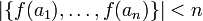 (כי יש שני איברים שנשלחים לאותו מקום) ואז
(כי יש שני איברים שנשלחים לאותו מקום) ואז  אינה על, שזו סתירה.
אינה על, שזו סתירה.
הערה: הדבר אינו נכון אם  ו-
ו- קבוצות אינסופיות. נסו למצוא דוגמה.
קבוצות אינסופיות. נסו למצוא דוגמה.
תרגיל
תהא  קבוצה. נגדיר פונקציה
קבוצה. נגדיר פונקציה 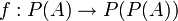 ע"י:
ע"י: 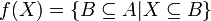 האם היא חח"ע? על?
האם היא חח"ע? על?
פתרון
חח"ע: כן. תהיינה 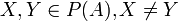 אם
אם 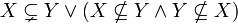 אזי
אזי 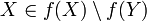 . אחרת
. אחרת 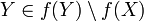 . כלומר
. כלומר 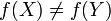 .
.
על: לא. נבחר 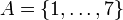 . למשל לקבוצה
. למשל לקבוצה 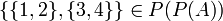 אין מקור. אין תת קבוצה שהאוסף הזה הוא בדיוק אוסף הקבוצות המכילות אותה.
אין מקור. אין תת קבוצה שהאוסף הזה הוא בדיוק אוסף הקבוצות המכילות אותה.
הרכבת פונקציות והפיכות
הגדרה:
יהיו 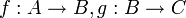 שתי פונקציות אזי ההרכבה של
שתי פונקציות אזי ההרכבה של  על
על  היא פונקציה
היא פונקציה 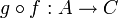 המוגדרת על ידי הכלל
המוגדרת על ידי הכלל 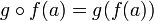 .
.
הערה: אם מתייחסים לפונקציות כאל יחסים - מקבלים את ההגדרה של הרכבת יחסים.
משפט:
- אם
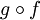 חח"ע אזי
חח"ע אזי  חח"ע.
חח"ע. - אם
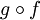 על אזי
על אזי  על.
על. - מסקנה: אם
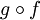 חח"ע ועל אזי
חח"ע ועל אזי  חח"ע ו-
חח"ע ו- על.
על.
תכונות של הרכבת פונקציות:
- הרכבה היא קיבוצית. כלומר
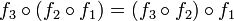 .
. - הרכבה אינה (בהכרח) חילופית כלומר לא מתקיים בהכרח כי
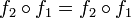 . למשל לפונקציות מעל הטבעיים
. למשל לפונקציות מעל הטבעיים 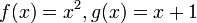 אזי
אזי 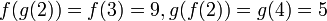 ולכן
ולכן 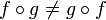 .
. - לכל פונקציה
 מתקיים
מתקיים 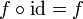 וגם
וגם 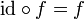 . שימו לב לתחומי ההגדרה והטווחים של הפונקציות שנדרשים כדי שהטענות האלו יהיו נכונות.
. שימו לב לתחומי ההגדרה והטווחים של הפונקציות שנדרשים כדי שהטענות האלו יהיו נכונות.
פונקציות הפיכות
הגדרה: תהי  פונקציה
פונקציה 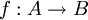 . פונקציה
. פונקציה 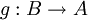 תקרא הפונקציה ההופכית ל-
תקרא הפונקציה ההופכית ל- אם
אם 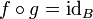 וגם
וגם 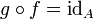 . במקרה זה נסמן את
. במקרה זה נסמן את  על ידי
על ידי 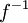 , ונאמר שהפונקציה
, ונאמר שהפונקציה  היא הפיכה.
היא הפיכה.
שימו לב שאם  פונקציה הפיכה, אז גם
פונקציה הפיכה, אז גם 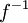 היא פונקציה הפיכה, ומתקיים
היא פונקציה הפיכה, ומתקיים 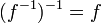 .
.
תרגיל
(לדלג, היה בהרצאה): הוכיחו כי פונקציה  הפיכה אם"ם היא חח"ע ועל.
הפיכה אם"ם היא חח"ע ועל.
פתרון
אם  הפיכה, אזי
הפיכה, אזי 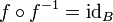 וגם
וגם 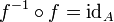 . מכיוון שפונקציית הזהות הינה חח"ע ועל, נובע ש-
. מכיוון שפונקציית הזהות הינה חח"ע ועל, נובע ש- חח"ע ועל לפי משפט קודם.
חח"ע ועל לפי משפט קודם.
אם  חח"ע ועל, אז נגדיר
חח"ע ועל, אז נגדיר 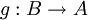 ע"י: עבור
ע"י: עבור 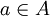 קיים (כי
קיים (כי  על)
על) 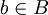 יחיד (כי
יחיד (כי  חח"ע) כך ש-
חח"ע) כך ש-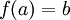 . נגדיר
. נגדיר 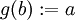 . תרגיל: בדקו כי
. תרגיל: בדקו כי  היא ההופכית של
היא ההופכית של  .
.
דוגמאות
- פונקציות
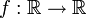 המוגדרות לפי:
המוגדרות לפי:
-
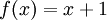 הפיכה וההופכית היא
הפיכה וההופכית היא 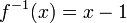 .
. -
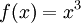 הפיכה וההופכית היא
הפיכה וההופכית היא 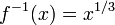 .
. -
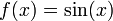 אינה הפיכה כי איננה חח"ע למשל
אינה הפיכה כי איננה חח"ע למשל 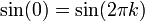 לכל
לכל 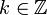 .
.
-
- תהא
 קבוצה. פונקציות
קבוצה. פונקציות 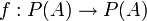 המוגדרות לפי:
המוגדרות לפי:
-
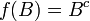 הפיכה וההופכית היא
הפיכה וההופכית היא 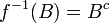 .
. - תהא
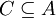 תת קבוצה.
תת קבוצה. 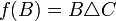 הפיכה וההופכית היא
הפיכה וההופכית היא 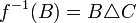 .
.
-
- תהא
 קבוצה. אזי אפשר (בעזרת חומר שראינו בתרגול על יחסי שקילות)
קבוצה. אזי אפשר (בעזרת חומר שראינו בתרגול על יחסי שקילות)
להגדיר 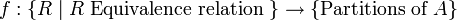 ע"י
ע"י 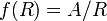 והיא תהיה חח"ע ועל, וכבר ראינו את הפונקציה ההופכית לה.
והיא תהיה חח"ע ועל, וכבר ראינו את הפונקציה ההופכית לה.
תרגיל
יהיו 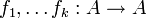 שכולן הפיכות\חח"ע\על. הוכיחו שההרכבה
שכולן הפיכות\חח"ע\על. הוכיחו שההרכבה 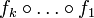 הפיכה\חח"ע\על.
הפיכה\חח"ע\על.
פתרון
למעשה אפשר לעשות אינדוקציה על המשפט מן ההרצאה.
חח"ע: נניח 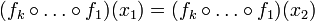 אזי מחח"ע של
אזי מחח"ע של 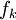 נקבל כי
נקבל כי 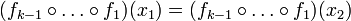 באופן דומה נמשיך (או באינדוקציה) ונקבל
באופן דומה נמשיך (או באינדוקציה) ונקבל 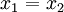 .
.
על: יהא 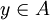 כיוון ש-
כיוון ש-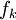 על, קיים
על, קיים 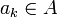 כך ש-
כך ש-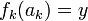 באותו אופן קיים
באותו אופן קיים 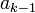 כך ש
כך ש 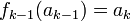 נמשיך באופן דומה (או באינקודציה)
ונקבל עיבוד הנוסחה נכשל (שגיאת תחביר): (f_k \circ \dots \circ f_1)(a_1)=(f_k \circ \dots \circ f_2)(a_2)=\\ \dots =f_k\circ f_{k-1} (a_{k-1}) = f_k(a_k)=y
נמשיך באופן דומה (או באינקודציה)
ונקבל עיבוד הנוסחה נכשל (שגיאת תחביר): (f_k \circ \dots \circ f_1)(a_1)=(f_k \circ \dots \circ f_2)(a_2)=\\ \dots =f_k\circ f_{k-1} (a_{k-1}) = f_k(a_k)=y
הפיכות: נובע מחח"ע יחד עם על.
תרגיל
הוכיחו כי אם 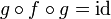 אז
אז  הפיכה.
הפיכה.
הוכחה:
הרכבה של פונקציה חח"ע 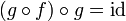 גורר שהפונקציה
גורר שהפונקציה  הימנית חח"ע.
הימנית חח"ע.
הרכבה של פונקציה על 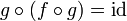 גורר שהפונקציה
גורר שהפונקציה  השמאלית על.
השמאלית על.
קיבלנו ש- חח"ע ועל, כלומר הפיכה. נכפול את הנתון ב-
חח"ע ועל, כלומר הפיכה. נכפול את הנתון ב-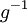 מימין ומשמאל ונקבל כי
מימין ומשמאל ונקבל כי 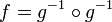 ואז
ואז  הפיכה כהרכבה של פונקציות הפיכות.
הפיכה כהרכבה של פונקציות הפיכות.