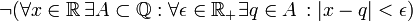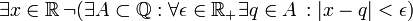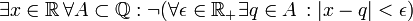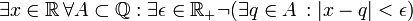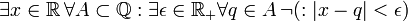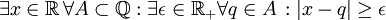הבדלים בין גרסאות בדף "תרגול 2 תשעז"

גרסה מ־13:14, 29 בנובמבר 2016

תוכן עניינים

1 כמתים ופרדיקטים
- 1.1 פרדיקטים
- 1.2 כמתים
2 שלילת פסוקים

כמתים ופרדיקטים

פרדיקטים

בניגוד לאטומים שהם ללא משתנים הפרדיקטים הינם פונקציות התלויות במשתנים. לדוגמא ניתן להגדיר את הפרדיקט 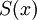$S(x)$ להיות x הינו סטודנט באוניברסיטה.

גם אטומים וגם פרדיקטים יכולים להיות אמיתיים (מסמנים 1 או T) או שקריים (מסמנים 0 או F). המינוח המקובל הוא שאטום/פרדיקט הוא בעל ערך אמת T (במידה שהוא נכון) או בעל ערך אמת F (במידה שאינו נכון).

כיוון שאטומים הם ללא משתנים הם יכולים להיות T או F אבל לא שניהם. לעומתם, פרדיקטים הם תלויים במשתנים ולכן ערך האמת שלהם יקבע לפי ההצבה במשתנים. למשל הפרדיקט 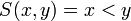$S(x,y)=x<y$ יהיה נכון במקרה ש 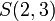$S(2,3)$ ולא נכון במקרה ש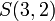 $S(3,2)$

כמתים

בנוסף, לקשרים ניתן להוסיף כמתים.

הכמת "לכל" 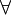$\forall$ והכמת "קיים"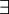 $\exist$

תפקיד מרכזי של הכמת הוא להבהיר את כוונת הטענה. למשל הטענה ש "סטונדט הוא יצור חרוץ" יכולה לקבל 2 משמעויות בעזרת הכמתים. או "כל סטודנט הוא יצור חרוץ" או "קיים סטודנט שהוא יצור חרוץ".

הטענה הראשונה טוענת לגבי כלל הסטודנטים (אם רוצים להוכיח כי הטענה נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם חרוצים ואם רוצים להוכיח כי הטענה לא נכונה מספיק למצוא סטודנט אחד שאינו חרוץ).

לעומתה הטענה השניה טוענת שניתן למצוא סטודנט אחד (לפחות) שהוא חרוץ (אם רוצים להוכיח את הטענה צריך למצוא סטודנט שהוא חרוץ ואם רוצים להוכיח כי הטענה לא נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם אינם חרוצים).

תרגיל: הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים).

פתרון: ההצרנה 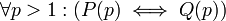$\forall p >1 : (P(p)\iff Q(p))$ כאשר

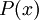$P(x)$ הוא הפרדיקט "x" הוא ראשוני.
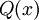$Q(x)$ הוא הפרדיקט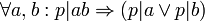 $\forall a,b : p|ab \Rightarrow (p|a \lor p|b)$

שלילת פסוקים

מהי השלילה של הפסוק "לכל סיר יש מכסה המתאים לו", או "לכל מאכל, יש מישהו שמכין אותו טעים"?

בעת שלילה של פסוק לוגי, הכמתים 'לכל' ו'קיים' מתחלפים זה עם זה, והשלילה עוברת הלאה. את השלילה על הקשרים ניתן לבצע באמצעות טאוטולוגיות וטבלאות אמת.

לדוגמא:

"לכל אדם בעולם קיים דג עם מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם"

השלילה היא:

"קיים אדם כך שלא קיים דג עם מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם"

נמשיך:

"קיים אדם שלכל דג בעולם לא נכון ש(יש לו מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם)"

כלומר

"קיים אדם שלכל דג בעולם יש מספר קשקשים שונה מגיל האדם וגם אורכו של הדג שונה מעשירית אורך האדם"

הערה: סדר הכמתים הוא חשוב (כמו בעברית) - לדוגמא: יש הבדל בין "לכל סיר קיים מכסה" לבין "קיים מכסה שמתאים לכל סיר".דוגמא: הצרן את המשפט "לכל מספר טבעי יש מספר טבעי הגדול ממנו" פתרון: 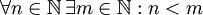$\forall n\in\mathbb{N}\,\exists m\in\mathbb{N}:n<m$ לעומת זאת 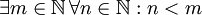$\exists m\in\mathbb{N}\,\forall n\in\mathbb{N}:n<m$ פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.

תרגיל: הצרן את המשפט "כל מספר ממשי ניתן לקרב ע"י מספרים רציונאליים בקירוב טוב כרצוננו"

פתרון: 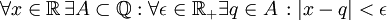$\forall x\in\mathbb{R}\,\exists A\subset\mathbb{Q}:\forall\epsilon\in\mathbb{R}_{+}\exists q\in A\,:|x-q|<\epsilon$ .

מה היא שלילתו של המשפט?

פתרון: נכתוב את הרמות השונות

$\neg(\forall x\in\mathbb{R}\,\exists A\subset\mathbb{Q}:\forall\epsilon\in\mathbb{R}_{+}\exists q\in A\,:|x-q|<\epsilon )$
$\exists x\in\mathbb{R}\,\neg( \exists A\subset\mathbb{Q}:\forall\epsilon\in\mathbb{R}_{+}\exists q\in A\,:|x-q|<\epsilon )$
$\exists x\in\mathbb{R}\, \forall A\subset\mathbb{Q}:\neg(\forall\epsilon\in\mathbb{R}_{+}\exists q\in A\,:|x-q|<\epsilon )$
$\exists x\in\mathbb{R}\, \forall A\subset\mathbb{Q}:\exists\epsilon\in\mathbb{R}_{+}\neg(\exists q\in A\,:|x-q|<\epsilon )$
$\exists x\in\mathbb{R}\, \forall A\subset\mathbb{Q}:\exists\epsilon\in\mathbb{R}_{+}\forall q\in A\,\neg(:|x-q|<\epsilon )$
$\exists x\in\mathbb{R}\,\forall A\subset\mathbb{Q}:\exists\epsilon\in\mathbb{R}_{+}\forall q\in A\,:|x-q|\geq\epsilon$

תרגילים: דוגמאות של הצרנת ושלילת המושגים 'תלות לינארית', 'גבול סדרה', 'חח"ע', וכדומה

@@ שורה 65: / שורה 65: @@
 תרגילים:
 דוגמאות של הצרנת ושלילת המושגים 'תלות לינארית', 'גבול סדרה', 'חח"ע', וכדומה
-==קבוצות קשרים שלמות==
-תרגיל: הוכח באמצעות טבלאות אמת שניתן להציג את הקשרים 'גרירה' ו'וגם' באמצעות 'או' ושלילה בלבד
-פתרון:
-מתקיים <math>A\to B \equiv \neg A \or B</math>
-ומתקיים <math>A \and B \equiv \neg(\neg A \or \neg B)</math>
-===צורות נורמליות: CNF ,DNF===
-ישנן שתי "צורות נורמליות" להצגת '''כל''' פסוקית - DNF ו CNF.
-===DNF===
-ביטוי בצורת DNF מורכב מאוסף "פסוקיות" המחוברות ביניהן על ידי פעולות "או".  כל פסוקית בעצמה מורכבת מאטומים המחוברים ביניהם על ידי פעולות "וגם". כל אטום הוא משתנה או שלילת משתנה.
-בצורה סכמטית: <math>D_1 \lor D_2 \lor \dots \lor D_n</math> כאשר כל <math>D_i</math> מהצורה <math>p_1\land p_2 \land \dots \land p_m</math> וכל <math>p_i</math> שווה למשתנה <math>x</math>
-או לשלילתו <math>\lnot x</math>.
-דוגמא: נמצא את צורת DNF של טבלת האמת הבאה:
-{| border="1" align="center" style="text-align:center;"
-|<math>f(x_1,x_2,x_3)</math>
-| <math>x_3</math>
-|<math>x_2</math>
-|<math>x_1</math>
-|-
-|0
-|0
-|0
-|0
-|-
-|0
-|0
-|0
-|1
-|-
-|1
-|0
-|1
-|0
-|-
-|1
-|1
-|0
-|0
-|-
-|0
-|0
-|1
-|1
-|-
-|1
-|1
-|0
-|1
-|-
-|0
-|1
-|1
-|0
-|-
-|0
-|1
-|1
-|1
-|-
-|}
-נתמקד בשורות שערך האמת שלהן הוא 1 (שורות 3, 4, 6).
-לשורה 3 נתאים את הפסוקית   <math>D_1=\lnot x_1 \land x_2 \land \lnot x_3</math>
-מה עשינו? החלפנו כל משתנה שערכו 0 בשלילה שלו, וכל משתנה שערכו 1 השארנו בלי לגעת.
-מה יצא לנו מזה? שימו לב שרק הצבה של ערכי האמת של <math>x_1,x_2,x_3</math> שמופיעים בשורה 3 תתן ערך אמת 1 ב <math>D_1</math>. כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 0 ב <math>D_1</math>.
-באופן דומה נייצר <math>D_2</math> עבור שורה 4 ו <math>D_3</math> עבור שורה 6:
-<math>D_2=\lnot x_1 \land\lnot x_2 \land x_3, \quad D_3=x_1\land \lnot x_2 \land x_3</math>
-כעת ה DNF של טבלת האמת היא פשוט
-<math>D_1\or D_2 \or D_3=(\lnot x_1 \land x_2 \land \lnot x_3) \or (\lnot x_1 \land \lnot x_2 \land x_3) \or (x_1 \land \lnot x_2 \land x_3)</math>.
-===CNF===
-ביטוי בצורת CNF מורכב מאוסף "פסוקיות" המחוברות ביניהן על ידי פעולות "וגם". כל פסוקית בעצמה מורכבת מאטומים המחוברים ביניהם על ידי פעולות "או". כל אטום הוא משתנה או שלילת משתנה.
-בצורה סכמטית: <math>C_1 \land C_2 \land \dots \land C_n</math> כאשר כל <math>C_i</math> מהצורה
-<math>q_1\lor q_2 \lor \dots \lor q_m</math> וכל <math>q_i</math> שווה למשתנה <math>x</math>
-או לשלילתו <math>\lnot x</math>.
-נדגים על הדוגמא לעיל.
-נתמקד בשורות שערך האמת שלהן הוא 0 (שורות 1, 2, 5, 7, 8)
-לשורה 1 נתאים את הפסוקית   <math>C_1= x_1 \lor x_2 \lor  x_3</math>
-מה עשינו? כל משתנה שערכו 0 השארנו בלי לגעת, וכל משתנה שערכו 1 החלפנו בשלילתו.
-מה יצא לנו מזה? שימו לב שרק הצבה של ערכי האמת של <math>x_1,x_2,x_3</math> שמופיעים בשורה 1 תתן ערך אמת 0 ב <math>C_1</math>. כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 1 ב <math>C_1</math>.
-באופן דומה נייצר <math>C_2,C_3,C_4,C_5</math> עבור שורות 2 , 5, 7 ו-8:
-<math>C_2= x_1 \lor \lnot x_2 \lor \lnot x_3, C_3=\lnot x_1\lor \lnot x_2 \lor x_3</math>
-<math> C_4=x_1 \lor \lnot x_2 \lor \lnot x_3, C_5= \lnot x_1 \lor \lnot x_2 \lor \lnot x_3</math>
-כעת ה CNF של טבלת האמת היא פשוט
-<math>C_1  \land C_2 \land C_3 \land C_4 \land C_5 </math>
-הרחבה על עניינים אלו (תרגול זה וקודמו) ניתן למצוא פה [[88-101 חשיבה מתמטית]]

הבדלים בין גרסאות בדף "תרגול 2 תשעז"

גרסה מ־13:14, 29 בנובמבר 2016

תוכן עניינים

כמתים ופרדיקטים

פרדיקטים

כמתים

שלילת פסוקים

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים