תרגול 5 מדמח קיץ תשעז
תוכן עניינים
יחסי סדר
הגדרה: יחס R על A נקרא אנטי-סימטרי אם מתקיים ![\forall x,y\in A:[(x,y)\in R]\and[(y,x)\in R] \rightarrow (x=y)](/images/math/b/2/7/b27500f5e820926a1e38f94ccc781069.png)
כלומר, אם 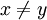 אז לא יכול להיות שמתקיים היחס בין x לבין y וגם היחס בין y לx.
אז לא יכול להיות שמתקיים היחס בין x לבין y וגם היחס בין y לx.
הגדרה: יחס R על A נקרא יחס סדר חלקי אם R רפלקסיבי, טרנזיטיבי ואנטי-סימטרי
דוגמאות ליחסי סדר חלקי:
- היחס 'קטן-שווה' על המספרים
- היחס 'מוכל-שווה' על הקבוצות
- היחס 'מחלק את ' על הטבעיים
נוכיח ש"מחלק את" על הטבעיים הינו יחס סדר חלקי:
רפלקסיבי: כל מספר מחלק את עצמו.
טרנזיטיבי: אם 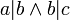 זאת אומרת ש-
זאת אומרת ש-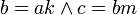 ולכן
ולכן 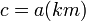 מה שאומר ש-
מה שאומר ש-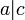 .
.
אנטי סימטרי: אם 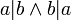 זאת אומרת ש-
זאת אומרת ש- 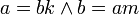 ולכן
ולכן 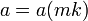 , כיון ש-
, כיון ש-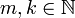 נקבל
נקבל 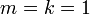 מה שאומר ש-
מה שאומר ש-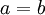 .
.
הערה: היחס "מחלק את" על השלמים איננו יחס סדר חלקי, כיון שמתקיים, למשל, ש- 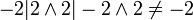 .
.
הגדרה. דיאגרמת הסה Hesse הינה דיאגרמה של יחס סדר חלקי על קבוצה. כל איבר המקושר לאיבר מתחתיו 'גדול' ממנו ביחס. נצייר את דיאגרמת הסה ליחס הכלה על קבוצת החזקה של הקבוצה 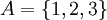 .
.
הגדרות. יהיו A קבוצה וR יחס סדר חלקי על הקבוצה:
- איבר
 נקרא מינמלי ביחס לR אם
נקרא מינמלי ביחס לR אם 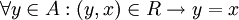 . כלומר, אין איבר 'קטן' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
. כלומר, אין איבר 'קטן' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו. - איבר
 נקרא מקסימלי ביחס לR אם
נקרא מקסימלי ביחס לR אם 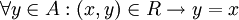 . כלומר, אין איבר 'גדול' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
. כלומר, אין איבר 'גדול' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו. - איבר
 נקרא קטן ביותר ביחס לR אם
נקרא קטן ביותר ביחס לR אם 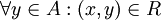 . כלומר, x 'קטן' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה הריקה תחת יחס הכלה)
. כלומר, x 'קטן' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה הריקה תחת יחס הכלה) - איבר
 נקרא גדול ביותר ביחס לR אם
נקרא גדול ביותר ביחס לR אם 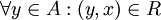 . כלומר, x 'גדול' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה B תחת יחס ההכלה על קבוצת החזקה של B)
. כלומר, x 'גדול' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה B תחת יחס ההכלה על קבוצת החזקה של B)
הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר קטן ביותר הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר לגבי הגדול ביותר.
הערה: מינימום 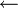 מינימלי, וכן מקסימום
מינימלי, וכן מקסימום 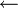 מקסימלי, ולא להיפך!
מקסימלי, ולא להיפך!
תרגיל
תהא  קבוצה ו
קבוצה ו יחס סדר חלקי מעליה. הוכח או הפרך: אם
יחס סדר חלקי מעליה. הוכח או הפרך: אם 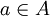 איבר מינימלי יחיד אז
איבר מינימלי יחיד אז  הוא קטן ביותר.
הוא קטן ביותר.
פתרון
הפרכה. דוגמה נגדית: נגדיר יחס  מעל
מעל 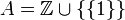 , בצורה הבאה:
, בצורה הבאה: 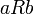 אם"ם
אם"ם 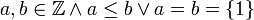 .
.
ראשית, צ"ל שזה יחס סדר חלקי:
רפלקסיביות: לכל 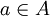 אם
אם 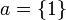 אזי לפי ההגדרה aRa וכן אם
אזי לפי ההגדרה aRa וכן אם 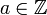 גם כן מתקיים aRa.
גם כן מתקיים aRa.
אנטי סמטריות: אם 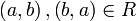 אזי אם
אזי אם 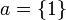 אזי לפי ההגדרה
אזי לפי ההגדרה 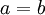 (כי
(כי  לא מתייחס לאף אחד אחר חוץ מלעצמו, לפי ההגדרה). אם
לא מתייחס לאף אחד אחר חוץ מלעצמו, לפי ההגדרה). אם 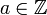 אזי בהכרח לפי הגדרת היחס גם
אזי בהכרח לפי הגדרת היחס גם 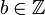 ואם
ואם 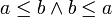 בשלמים אז בהכרח
בשלמים אז בהכרח 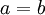 .
.
טרנזטיביות: אם 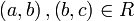 אזי אם
אזי אם 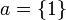 אזי לפי ההגדרה
אזי לפי ההגדרה 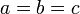 וכמובן
וכמובן 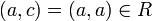 . אם
. אם 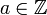 אזי בהכרח לפי הגדרת היחס גם
אזי בהכרח לפי הגדרת היחס גם 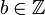 ולכן גם
ולכן גם 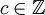 ומתקיים
ומתקיים 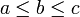 ובפרט
ובפרט 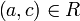 .
.
כעת, נראה שיש מינימלי יחיד שאינו קטן ביותר: 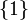 הוא איבר מינימלי יחיד בקבוצה. מינימלי כי פרט לעצמו אף איבר לא ניתן להשוואה עימו, ולכן אין שונה ממנו שקטן ממנו, ואין עוד מינימלי כי
הוא איבר מינימלי יחיד בקבוצה. מינימלי כי פרט לעצמו אף איבר לא ניתן להשוואה עימו, ולכן אין שונה ממנו שקטן ממנו, ואין עוד מינימלי כי 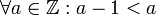 . הוא לא הקטן ביותר כי אף איבר לא ניתן להשוואה עימו, וכלן לא מתקיים שהוא קטן מכולם (הוא לא קטן מאף שלם).
. הוא לא הקטן ביותר כי אף איבר לא ניתן להשוואה עימו, וכלן לא מתקיים שהוא קטן מכולם (הוא לא קטן מאף שלם).
הערה: 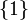 הוא גם מקסימלי יחיד שאינו גדול ביותר.
הוא גם מקסימלי יחיד שאינו גדול ביותר.
דוגמא
נביט בקבוצה 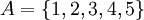 ונגדיר עליה יחס סדר חלקי:
ונגדיר עליה יחס סדר חלקי:
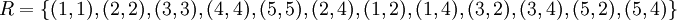
(הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם)
- 5,3,1 הינם איברים מינימליים שכן אין איבר שקטן מאף אחד מהם. הם אינם מינימום כי אף אחד מהם לא קטן מכל האיברים האחרים.
- 4 הינו מקסימום של הקבוצה, הוא בוודאי מקסימלי
- 2 קטן מחלק מהאיברים וגדול מאחרים לכן הוא כלום.
הגדרות. תהי A קבוצה, ותהי B קבוצה המוכלת בה ויהי R יחס סדר חלקי:
- חסם מלעיל של B הוא איבר
 כך שמתקיים
כך שמתקיים 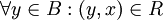
- חסם מלרע של B הוא איבר
 כך שמתקיים
כך שמתקיים 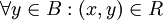
- החסם העליון (סופרמום) של B הינו האיבר הקטן ביותר בקבוצת חסמי המלעיל (אם קיים). מסומן
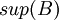
- החסם התחתון (אינפימום) של B הינו האיבר הגדול ביותר בקבוצת חסמי המלרע (אם קיים). מסומן
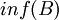
דוגמאות
דוגמא.
נשוב לדוגמא הקודמת. נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד 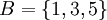 . קבוצת חסמי המלעיל של B הינה
. קבוצת חסמי המלעיל של B הינה 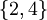 . המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
. המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
דוגמא.
נביט במספרים הממשיים ובתת הקבוצה של כל המספרים עם מספר סופי של ספרות ששווים לספרות הראשונות של שורש 2. 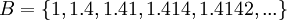 . חסמי המלעיל של הקבוצה הינם כל המספרים שגדולים או שווים לשורש 2 ואילו שורש 2 הוא החסם העליון של הקבוצה.
. חסמי המלעיל של הקבוצה הינם כל המספרים שגדולים או שווים לשורש 2 ואילו שורש 2 הוא החסם העליון של הקבוצה.
שימו לב, אם נביט בקבוצה B כתת קבוצה של המספרים הרציונאליים, חסמי המלעיל שלה יהיו כל האיברים הגדולים משורש 2 אך מכיוון ששורש 2 אינו רציונאלי, אין לB חסם עליון.
דוגמא. נביט בקבוצת הטבעיים, ובתת קבוצה סופית שלה B. נביט ביחס "מחלק את". הסופרמום של B הוא המכפלה המשותפת המינימלית (lcm), והאינפימום הוא המחלק המשותף המקסימלי(gcd).
למשל 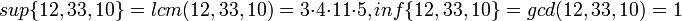
תרגיל
הוכיחו: אם  חסם מלרע של
חסם מלרע של  וגם
וגם 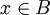 אזי
אזי 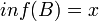 (וגם ב B יש איבר קטן ביותר
שהוא x).
(וגם ב B יש איבר קטן ביותר
שהוא x).
פתרון
צריך להראות ש-  גדול ביותר בקבוצת חסמי המלרע של
גדול ביותר בקבוצת חסמי המלרע של  . יהי
. יהי  חסם מלרע של
חסם מלרע של  , לכן, לכל
, לכן, לכל 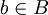 מתקיים ש-
מתקיים ש- 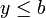 , ובפרט עבור
, ובפרט עבור 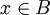 נקבל
נקבל 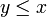 . זוהי בדיוק ההגדרה של גדול ביותר.
. זוהי בדיוק ההגדרה של גדול ביותר.
בנוסף, יהי 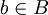 , כיון ש-
, כיון ש- חסם מלרע נקבל
חסם מלרע נקבל 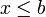 , ולכן
, ולכן  קטן ביותר ב-
קטן ביותר ב- .
.
הגדרה. יהי R יחס סדר חלקי על A. אם לכל שני איברים a,b בA מתקיים ![[(a,b)\in R]\or[(b,a)\in R]](/images/math/1/d/4/1d4d3394750a0b97771353ed8775b927.png) אזי R נקרא יחס סדר מלא.
אזי R נקרא יחס סדר מלא.
תרגיל ממבחן
הגדרה: תת קבוצה A של המספרים הממשיים נקראת 'מגניבה' אם לכל x,y בA כך ש-x שונה מ-y מתקיים שההפרש x-y אינו רציונאלי.
תהי B קבוצה מגניבה מקסימלית ביחס להכלה, הוכח שלכל מספר ממשי שאינו שייך לB קיים איבר בB כך שההפרש בינהם הוא רציונאלי.
הוכחה.
נניח בשלילה שקיים איבר ממשי r שאינו בB, ולכל איבר b ב-B ההפרש r-b אינו רציונאלי. לכן אם נוסיף את r ל-B נקבל קבוצה מגניבה המכילה ממש את B (ולא שווה לה) בסתירה למקסימאליות של B.
יחס סדר מילוני
יהיו 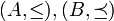 שתי קבוצות סדורות חלקית.
שתי קבוצות סדורות חלקית.
על 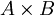 ניתן להגדיר את היחס המילוני
ניתן להגדיר את היחס המילוני  ע"י
ע"י
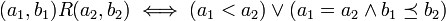
דוגמא
נסתכל על 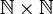 אם הסדר המילוני.
אם הסדר המילוני.
נגדיר 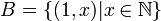 אזי
אזי 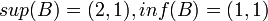
נגדיר 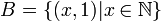 אזי
אזי 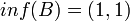 ו sup לא קיים.
ו sup לא קיים.
- שימו לב ש
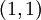 הוא איבר קטן ביותר
הוא איבר קטן ביותר
מכפלה של יחסי סדר
יהיו 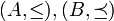 שתי קבוצות סדורות חלקית.
שתי קבוצות סדורות חלקית.
על 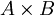 ניתן להגדיר את היחס
ניתן להגדיר את היחס  הבא:
הבא:
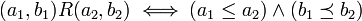
זהו יחס סדר:
הוכחה:
1. רפקלסיביות: לכל 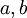 מתקיים כי $a\leq a, b\preceq b$ ולכן
מתקיים כי $a\leq a, b\preceq b$ ולכן 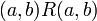
2. אנטי סימטריות: אם 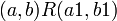 וגם
וגם 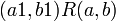 אז
אז 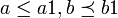 וגם
וגם 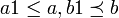 , כיוון שאלו יחס סדר נקבל כי
, כיוון שאלו יחס סדר נקבל כי 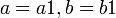
3. טרנז' - תרגיל
דוגמא
נסתכל על 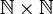 אם הסדר המוגדר לעיל.
אם הסדר המוגדר לעיל.
נגדיר 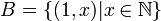 אזי
אזי 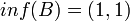 ו sup לא קיים
ו sup לא קיים
נגדיר 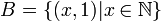 אזי
אזי 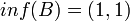 ו sup לא קיים.
ו sup לא קיים.
- שימו לב ש
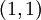 הוא איבר קטן ביותר
הוא איבר קטן ביותר
תרגיל (ממבחן קיץ תשעה מועד ב)
תהא 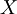 קבוצת כל הסדרות הבינאריות (סדרה בינארית היא
קבוצת כל הסדרות הבינאריות (סדרה בינארית היא 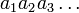 כאשר
כאשר 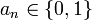 ). נגדיר יחס
). נגדיר יחס  על
על 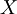 כך:
עבור
כך:
עבור 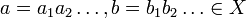
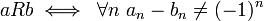
א. הוכיחו ש  יחס סדר על
יחס סדר על 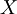
ב. קבעו האם  יחס סדר מלא על
יחס סדר מלא על 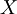
ג. מצאו (אם קיימים) איבר קטן וגדול ביותר ב 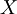 (ביחס ל
(ביחס ל  )
)
פתרון
דרך שקולה לתאר את היחס שמפשטת את השאלה היא כך
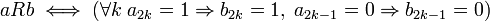
כלומר במיקומים הזוגיים, אם a שווה 1 אז זה גורר ש b שווה 1
ובמיקומים האי זוגיים, אם a שווה 0 אז זה גורר ש b שווה 0
א. תרגיל לבד!
ב. לא סדר מלא, למשל 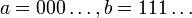 לא מתייחסים זה לזה.
לא מתייחסים זה לזה.
ג. קימיים, 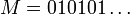 הינו איבר הגדול ביותר כי לכל
הינו איבר הגדול ביותר כי לכל  מתקים
מתקים 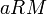
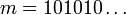 הינו איבר קטן ביותר כי לכל
הינו איבר קטן ביותר כי לכל  מתקים
מתקים 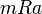
תרגיל (מבוחן תשעג)
יהא  קבוצה ו
קבוצה ו 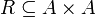 יחס סדר מלא עליה. נגדיר
יחס סדר מלא עליה. נגדיר 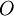 להיות קבוצת כל יחסי הסדר החלקיים על
להיות קבוצת כל יחסי הסדר החלקיים על  , סדורה ע"י הכלה. (כלומר הזוג
, סדורה ע"י הכלה. (כלומר הזוג 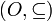 - במילים אחרות, חושבים על
- במילים אחרות, חושבים על 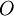 עם יחס הסדר החלקי "הכלה")
עם יחס הסדר החלקי "הכלה")
הוכח:  איבר מקסימלי ב
איבר מקסימלי ב 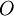
פתרון- יהי 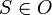 יחס סדר חלקי על
יחס סדר חלקי על  המקיים
המקיים 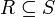 צ"ל
צ"ל 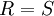
נניח בשלילה כי  מוכל ממש ב
מוכל ממש ב 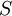
אזי קיים 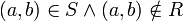 . כיוון ש
. כיוון ש  יחס מלא אזי מתקיים
יחס מלא אזי מתקיים 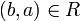 כיוןן ש
כיוןן ש 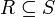 נובע כי
נובע כי 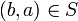
מכיוון ש 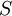 יחס סדר חלקי (בפרט אנטי סימטרי) אזי
יחס סדר חלקי (בפרט אנטי סימטרי) אזי 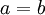 (כי גם (
(כי גם (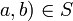 )
אזי קיבלנו כי ּ
)
אזי קיבלנו כי ּ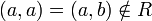 סתירה לכך ש
סתירה לכך ש  יחס סדר מלא ובפרט רפלקסיבי.
יחס סדר מלא ובפרט רפלקסיבי.
האם ב 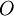 יש מקסימום (איבר גדול ביותר)?
יש מקסימום (איבר גדול ביותר)?
תשובה: לא. נניח שקיים איבר מקס' 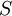 . כיוון שגם
. כיוון שגם 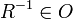 יחס אזי
יחס אזי 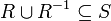 . בפרט אם
. בפרט אם 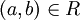 שונים (נניח שב
שונים (נניח שב  יש 2 איברים לפחות) אזי
יש 2 איברים לפחות) אזי 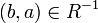 ולכן
ולכן 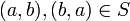 בניגוד לכך ש
בניגוד לכך ש 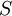 אנטי סימטרי
אנטי סימטרי