הבדלים בין גרסאות בדף "תרגילי חובה לא סטנדרטיים"
מתוך Math-Wiki
(←חשבון אינפיניטיסימלי) |
|||
| (6 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 8: | שורה 8: | ||
== חשבון אינפיניטיסימלי == | == חשבון אינפיניטיסימלי == | ||
| − | * אי-שוויון הממוצעים | + | '''חשבון במשתנה ממשי יחיד''' |
| − | * | + | * אי-שוויון הממוצעים: לכל קבוצה של מספרים ממשיים חיובים <math>\{a_1,\dots,a_n\}</math> מתקיים אי השיוויון <math>\frac{n}{\frac{1}{x_1}+\dots+\frac{1}{x_n}}\le\sqrt[n]{x_1\cdots x_n}\le\frac{\sum_{k=1}^nx_k}{n}</math>. יש שיוויון אם"ם כל האיברים שווים האחד לשני. |
| − | * | + | * הלמה של Fekete: אם <math>a_n</math> סדרה תת-אדיטיבית, אז ל-<math>\frac{a_n}{n}</math> יש גבול במובן הרחב השווה ל<math>\inf a_n</math>). |
| − | * | + | * המשפט של Stolz-Cesàro: אם <math>b_n</math> סידרה חיובית כך ש<math>\sum_n b_n=\infty</math> אז לכל סידרה <math>a_n</math>, <math>\limsup \frac{a_n}{b_n}\ge\limsup\frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge\liminf \frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge \liminf \frac{a_n}{b_n}</math>. |
| − | * | + | * קירוב Stirling: <math>\Gamma(n+1)=n!\approx \sqrt{2\pi n}\left(\frac ne\right)^n</math>. |
| + | * סומביליות Abel: אם הסכום <math>\sum_n a_n</math> קיים אז גם <math>\sum_{r\to 1^-} \sum a_n r^n</math> קיים ושווה לו; אבל יש טורים המתכנסים בסומביליות זו אך לא במובן הרגיל. | ||
| + | * סומביליות Cesàro: לכל סדרה מתכנסת גם סדרת הממוצעים החשבוניים מתכנסת ולאותו ערך, אבל יש סדרות שהממוצעים שלהן מתכנסים אולם הן לא. סומביליות Abel גוררת סומביליות Cesàro. | ||
| + | * משפט Tauber: אם הטור <math>\sum a_n</math> סכים-Abel ו<math>a_n=o(\frac1n)</math> אז <math>\sum_n a_n=\lim_{r\to 1^-}\sum_{n=0}^\infty a_n r^n</math>. | ||
| + | * הלמה של Reimann-Lebesgue: אם <math>f\in \mathcal{R}([a,b])</math> אז <math>\int_a^b f(x)\sin(nx)dx,\int_a^b f(x)\cos(nx)dx\overset{\left|n\right|\to\infty}{\longrightarrow}0</math> (כלומר מקדמי הFourier שלה דועכים). | ||
== תורת החבורות == | == תורת החבורות == | ||
* יש אינסוף ראשוניים. יש אינסוף ראשוניים מהצורה 4n-1. יש אינסוף ראשוניים מהצורה 4n+1. | * יש אינסוף ראשוניים. יש אינסוף ראשוניים מהצורה 4n-1. יש אינסוף ראשוניים מהצורה 4n+1. | ||
גרסה אחרונה מ־04:57, 22 בדצמבר 2016
תרגילים שעלולים לשכוח ולא כדאי:
אלגברה לינארית
- חישוב הדטרמיננטה של מטריצת ונדרמונדה
- אין מטריצה אנטי-סימטרית הפיכה מממד אי-זוגי
חשבון אינפיניטיסימלי
חשבון במשתנה ממשי יחיד
- אי-שוויון הממוצעים: לכל קבוצה של מספרים ממשיים חיובים
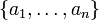 מתקיים אי השיוויון
מתקיים אי השיוויון ![\frac{n}{\frac{1}{x_1}+\dots+\frac{1}{x_n}}\le\sqrt[n]{x_1\cdots x_n}\le\frac{\sum_{k=1}^nx_k}{n}](/images/math/9/b/b/9bb587ddf0cf9d457c1a67f5ed29595a.png) . יש שיוויון אם"ם כל האיברים שווים האחד לשני.
. יש שיוויון אם"ם כל האיברים שווים האחד לשני. - הלמה של Fekete: אם
 סדרה תת-אדיטיבית, אז ל-
סדרה תת-אדיטיבית, אז ל-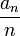 יש גבול במובן הרחב השווה ל
יש גבול במובן הרחב השווה ל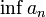 ).
). - המשפט של Stolz-Cesàro: אם
 סידרה חיובית כך ש
סידרה חיובית כך ש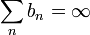 אז לכל סידרה
אז לכל סידרה  ,
, 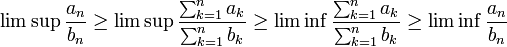 .
. - קירוב Stirling:
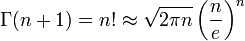 .
. - סומביליות Abel: אם הסכום
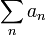 קיים אז גם
קיים אז גם 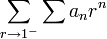 קיים ושווה לו; אבל יש טורים המתכנסים בסומביליות זו אך לא במובן הרגיל.
קיים ושווה לו; אבל יש טורים המתכנסים בסומביליות זו אך לא במובן הרגיל. - סומביליות Cesàro: לכל סדרה מתכנסת גם סדרת הממוצעים החשבוניים מתכנסת ולאותו ערך, אבל יש סדרות שהממוצעים שלהן מתכנסים אולם הן לא. סומביליות Abel גוררת סומביליות Cesàro.
- משפט Tauber: אם הטור
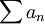 סכים-Abel ו
סכים-Abel ו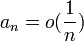 אז
אז 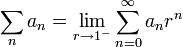 .
. - הלמה של Reimann-Lebesgue: אם
![f\in \mathcal{R}([a,b])](/images/math/b/d/2/bd21d1c7bf9271074499100736de23ee.png) אז
אז 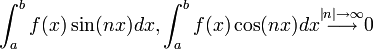 (כלומר מקדמי הFourier שלה דועכים).
(כלומר מקדמי הFourier שלה דועכים).
תורת החבורות
- יש אינסוף ראשוניים. יש אינסוף ראשוניים מהצורה 4n-1. יש אינסוף ראשוניים מהצורה 4n+1.