הבדלים בין גרסאות בדף "84-172 מתמטיקה לכימאים ב/סילבוס"
מתוך Math-Wiki
(←העתקות לינאריות) |
(←מטריצות) |
||
| שורה 64: | שורה 64: | ||
*מציאת בסיס לתמונה. | *מציאת בסיס לתמונה. | ||
| + | *כפל מטריצות. | ||
*מטריצות הופכיות. | *מטריצות הופכיות. | ||
גרסה מ־07:18, 20 באפריל 2021
תוכן עניינים
מבחנים לדוגמא
לוח ההרצאות
נושאי הרצאות
כאן יופיעו נושאי ההרצאות המשוערים לסמסטר.
חלק 1: וקטורים ופונקציות לינאריות
שדות
- מושג השדה, המספרים המרוכבים
להרחבה ראו פרק 1 בקישור https://linear.math-wiki.com
מרחבים וקטוריים ומכפלה פנימית
- מרחבים וקטוריים (חיבור וקטורים וכפל בסקלר)
- מכפלה פנימית (סקלרית) והנורמה המושרית.
- נבחן כל אחת מהפעולות באופן אלגברי ובאופן גאומטרי.
- אי שיוויון קושי-שוורץ
העתקות לינאריות
- פונקציות לינאריות
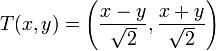 סיבוב נגד כיוון השעון בזוית 45 מעלות.
סיבוב נגד כיוון השעון בזוית 45 מעלות.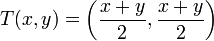 היטל על הישר y=x.
היטל על הישר y=x.
- גרעין ותמונה (מקיימים תכונות של תתי מרחב)
- בסיס לגרעין או תמונה היא קבוצת וקטורים המייצרת את הקבוצה, ואין בה דבר מיותר.
- מימד הוא מספר האיברים בבסיס.
חלק 2: מטריצות
מטריצות
- הצגת פונקציות לינאריות באמצעות מטריצות
- גרעין זו ההצגה האלגברית, תמונה היא ההצגה הפרמטרית של ישרים ומישורים.
- פתרון מערכות משוואות באמצעות מטריצות (מציאת בסיס).
- דרגת מטריצה.
- מציאת בסיס לתמונה.
- כפל מטריצות.
- מטריצות הופכיות.
לכסון מטריצות
- מהו לכסון מטריצות ולמה הוא טוב (למשל העלאת מטריצה בחזקה).
- פולינום אופייני, ערכים עצמיים, וקטורים עצמיים.
- אלגוריתם ללכסון מטריצה.
חלק 3: חדו"א בשני משתנים
מבוא
- גרף מהצורה
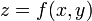
- גבולות ורציפות
גזירות
- נגזרות חלקיות
- דיפרנציאביליות
- מישור משיק
- נגזרות כיווניות והגרדיאנט
- כלל השרשרת ומד"ר מדוייקת
בעיות קיצון
- קיצון מקומי
- קיצון עם אילוץ
חלק 4: אינטגרלים כפולים ומשולשים
- אינטגרלים כפולים ומשולשים ומשמעותם
- החלפת סדר האינטגרציה
- שינוי קואורדינטות