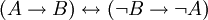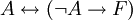הבדלים בין גרסאות בדף "88-101 חשיבה מתמטית קיץ תשעא/תרגילים/פתרון 1"
מתוך Math-Wiki
(יצירת דף עם התוכן "===הצרנות=== *הצרן את הטענות הבאות (מותר לכם להשתמש בפרדיקטים סבירים, בתנאי שתגדירו אותם): **לכ...") |
(←דרכי הוכחה) |
||
| (5 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
===הצרנות=== | ===הצרנות=== | ||
| − | + | ||
**לכל מספר ממשי יש מספר טבעי הגדול ממנו. | **לכל מספר ממשי יש מספר טבעי הגדול ממנו. | ||
| + | <math>\forall x\in\mathbb{R}\exists n\in\mathbb{N}:n>x</math> | ||
| + | |||
| + | |||
**אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (<math>P(1)\equiv T</math>) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד. | **אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (<math>P(1)\equiv T</math>) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד. | ||
| + | <math>\Big[P(1)\and (\forall n\in\mathbb{N}:P(n)\rightarrow P(n+1))\Big]\rightarrow\forall n\in\mathbb{N}:P(n)</math> | ||
| + | |||
| + | |||
**x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד). | **x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד). | ||
| + | נגדיר את הפרדיקט בעל שני המשתנים "x מחלק את y" ונסמן אותו באופן הנהוג <math>x|y</math>. לכן x ראשוני אם <math>\forall n\in\mathbb{N}: (n|x)\rightarrow ((n=1)\or(n=x))</math> | ||
| + | |||
| + | |||
**כל מספר ראשוני הינו סכום של מספרים זוגיים. | **כל מספר ראשוני הינו סכום של מספרים זוגיים. | ||
| + | <math>\forall x\in\mathbb{N}:\Big[\forall n\in\mathbb{N}: (n|x)\rightarrow ((n=1)\or(n=x))\Big]\rightarrow \Big[\exists n\in\mathbb{N}\exists k\in\mathbb{N}:2n+2k=x\Big]</math> | ||
| + | |||
| + | |||
**קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.) | **קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.) | ||
| + | "קיימים אינסוף" הוא תנאי שיש להגדיר. ההגדרה האינטואיטיבית הינה לא קיים מספר סופי של איברים כאלה, כלומר ההנחה שיש מספר סופי תוביל לשלילה. הראנו בתרגיל אחר שזה שקול לטענה לכל מספר יש מספר הגדול ממנו המקיים את התנאי, וזה מה שנצרין כאן. | ||
| + | |||
| + | <math>\forall n\in\mathbb{N}\exists x\in\mathbb{N}:\Big[x>n\Big]\and\Big[\forall k\in\mathbb{N}: (k|x)\rightarrow ((k=1)\or(k=x))\Big] \and \Big[\forall k\in\mathbb{N}: (k|x+2)\rightarrow ((k=1)\or(k=x+2))\Big]</math> | ||
===קבוצות=== | ===קבוצות=== | ||
| − | |||
*הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB | *הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB | ||
| + | <math>x\in A\cup B \iff (x\in A) \or (x\in B)</math> | ||
| + | |||
| + | |||
*הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB | *הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB | ||
| + | <math>x\notin A\cup B \iff \neg\Big[(x\in A) \or (x\in B)\Big]\iff (x\notin A) \and (x\notin B)</math> | ||
| + | |||
| + | |||
*הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB | *הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB | ||
| + | <math>x\in A\cap B \iff (x\in A) \and (x\in B)</math> | ||
| + | |||
| + | |||
*הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB | *הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB | ||
| + | <math>x\notin A\cap B \iff \neg\Big[(x\in A) \and (x\in B)\Big]\iff (x\notin A) \or (x\notin B)</math> | ||
| + | |||
| − | |||
*הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB | *הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB | ||
| − | + | <math>C\subseteq (A\cap B)\iff \forall c\in C: c\in (A\cap B) \iff \forall c\in C: (c\in A) \and (c\in B)</math> | |
| − | + | *הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB | |
| + | <math>\neg\Big[C\subseteq (A\cap B)\Big]\iff \neg\Big[\forall c\in C: (c\in A) \and (c\in B)\Big]\iff \exists c\in C: (c\notin A)\or (c\notin B)</math> | ||
===שקילות=== | ===שקילות=== | ||
| − | |||
*הוכח שמספיק להוכיח את הטענות הבאות על מנת להוכיח ש<math>A_1,A_2,...,A_n</math> שקולות: | *הוכח שמספיק להוכיח את הטענות הבאות על מנת להוכיח ש<math>A_1,A_2,...,A_n</math> שקולות: | ||
| שורה 34: | שורה 58: | ||
<math>A_n\rightarrow A_1</math> | <math>A_n\rightarrow A_1</math> | ||
| + | |||
| + | |||
| + | *הוכחה: | ||
| + | נניח שהטענות שקולות ונניח ש<math>A_i</math> אמיתית. לכן <math>A_{i+1}</math> חייבת להיות אמיתית, לכן <math>A_{i+2}</math> גם וכן הלאה עד <math>A_n</math> זה גורר את נכונות <math>A_1</math> וכך הלאה עד שנגיע לכל הטענות. | ||
| + | |||
| + | לכן, אם טענה אחת אמיתית, כולן אמיתיות. נובע בקלות שאם אחת תהא שקרית, לא ייתכן שאף אחת אחרת תהא אמיתית ולכן כולם אמיתיות ושקריות יחדיו. | ||
===דרכי הוכחה=== | ===דרכי הוכחה=== | ||
| שורה 41: | שורה 71: | ||
| − | + | התשובה הינה בדיקה קלה בטבלת אמת. | |
גרסה אחרונה מ־06:25, 5 באוגוסט 2011
תוכן עניינים
הצרנות
- לכל מספר ממשי יש מספר טבעי הגדול ממנו.
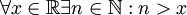
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
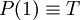 ) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
![\Big[P(1)\and (\forall n\in\mathbb{N}:P(n)\rightarrow P(n+1))\Big]\rightarrow\forall n\in\mathbb{N}:P(n)](/images/math/1/3/6/13698cfc11b7ebb897083ddd73930f54.png)
- x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד).
נגדיר את הפרדיקט בעל שני המשתנים "x מחלק את y" ונסמן אותו באופן הנהוג 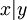 . לכן x ראשוני אם
. לכן x ראשוני אם 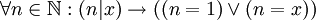
- כל מספר ראשוני הינו סכום של מספרים זוגיים.
![\forall x\in\mathbb{N}:\Big[\forall n\in\mathbb{N}: (n|x)\rightarrow ((n=1)\or(n=x))\Big]\rightarrow \Big[\exists n\in\mathbb{N}\exists k\in\mathbb{N}:2n+2k=x\Big]](/images/math/e/8/9/e89caa7ac3bb48b1dad3c95da807bd07.png)
- קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.)
"קיימים אינסוף" הוא תנאי שיש להגדיר. ההגדרה האינטואיטיבית הינה לא קיים מספר סופי של איברים כאלה, כלומר ההנחה שיש מספר סופי תוביל לשלילה. הראנו בתרגיל אחר שזה שקול לטענה לכל מספר יש מספר הגדול ממנו המקיים את התנאי, וזה מה שנצרין כאן.
![\forall n\in\mathbb{N}\exists x\in\mathbb{N}:\Big[x>n\Big]\and\Big[\forall k\in\mathbb{N}: (k|x)\rightarrow ((k=1)\or(k=x))\Big] \and \Big[\forall k\in\mathbb{N}: (k|x+2)\rightarrow ((k=1)\or(k=x+2))\Big]](/images/math/3/a/9/3a98dfc726b858886a0259a81f6ea588.png)
קבוצות
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
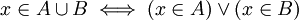
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
![x\notin A\cup B \iff \neg\Big[(x\in A) \or (x\in B)\Big]\iff (x\notin A) \and (x\notin B)](/images/math/4/2/6/4267aba5814ee2b9434827da07ed133e.png)
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
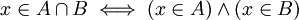
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
![x\notin A\cap B \iff \neg\Big[(x\in A) \and (x\in B)\Big]\iff (x\notin A) \or (x\notin B)](/images/math/6/8/8/688f6dab28cf8694ce41cdc64e36a144.png)
- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
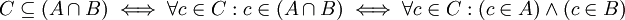
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
![\neg\Big[C\subseteq (A\cap B)\Big]\iff \neg\Big[\forall c\in C: (c\in A) \and (c\in B)\Big]\iff \exists c\in C: (c\notin A)\or (c\notin B)](/images/math/f/1/2/f12c41b86eb801b36b576ddd912d3701.png)
שקילות
- הוכח שמספיק להוכיח את הטענות הבאות על מנת להוכיח ש
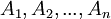 שקולות:
שקולות:
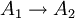 ,
,
 ,
,
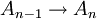 ,
,
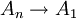
- הוכחה:
נניח שהטענות שקולות ונניח ש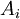 אמיתית. לכן
אמיתית. לכן 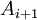 חייבת להיות אמיתית, לכן
חייבת להיות אמיתית, לכן 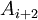 גם וכן הלאה עד
גם וכן הלאה עד 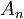 זה גורר את נכונות
זה גורר את נכונות 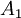 וכך הלאה עד שנגיע לכל הטענות.
וכך הלאה עד שנגיע לכל הטענות.
לכן, אם טענה אחת אמיתית, כולן אמיתיות. נובע בקלות שאם אחת תהא שקרית, לא ייתכן שאף אחת אחרת תהא אמיתית ולכן כולם אמיתיות ושקריות יחדיו.
דרכי הוכחה
הוכח שהפסוקים הבאים הינם טאוטולוגיות:
התשובה הינה בדיקה קלה בטבלת אמת.