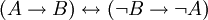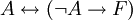הצרנות
- לכל מספר ממשי יש מספר טבעי הגדול ממנו.
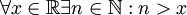
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
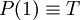 ) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
![\Big[P(1)\and (\forall n\in\mathbb{N}:P(n)\rightarrow P(n+1))\Big]\rightarrow\forall n\in\mathbb{N}:P(n)](/images/math/1/3/6/13698cfc11b7ebb897083ddd73930f54.png)
- x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד).
נגדיר את הפרדיקט בעל שני המשתנים "x מחלק את y" ונסמן אותו באופן הנהוג 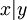 . לכן x ראשוני אם
. לכן x ראשוני אם 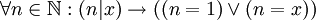
- כל מספר ראשוני הינו סכום של מספרים זוגיים.
![\forall x\in\mathbb{N}:\Big[\forall n\in\mathbb{N}: (n|x)\rightarrow ((n=1)\or(n=x))\Big]\rightarrow \Big[\exists n\in\mathbb{N}\exists k\in\mathbb{N}:2n+2k=x\Big]](/images/math/e/8/9/e89caa7ac3bb48b1dad3c95da807bd07.png)
- קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.)
קבוצות
הגדרה: איחוד של שתי קבוצות A וB הוא קבוצת האיברים שנמצאים לפחות באחת הקבוצות. החיתוך הוא קבוצת האיברים שנמצאים בשתי הקבוצות.
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
הגדרה: קבוצה A מוכלת בקבוצה B אם בB נמצאים כל האיברים מA (למשל הטבעיים מוכלים בשלמים 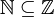 , והשלמים מוכלים בממשיים
, והשלמים מוכלים בממשיים 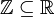 ).
).
- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
(מותר לכם להשתמש בכמתים באופן הבא 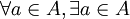 )
)
שקילות
הגדרה: טענות 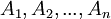 שקולות אם ((כולן אמיתיות יחד) או (כולן שקריות יחד)).
שקולות אם ((כולן אמיתיות יחד) או (כולן שקריות יחד)).
- הוכח שמספיק להוכיח את הטענות הבאות על מנת להוכיח ש
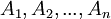 שקולות:
שקולות:
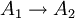 ,
,
 ,
,
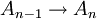 ,
,
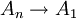
דרכי הוכחה
הוכח שהפסוקים הבאים הינם טאוטולוגיות:
(נהוג להחליף ביטויים מהצורה הזו בביטויים השקולים להם כי הם נוחים יותר להוכחה מידי פעם.)