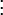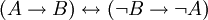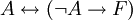הצרנות
- לכל מספר ממשי יש מספר טבעי הגדול ממנו.
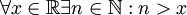
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
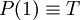 ) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
![\Big[P(1)\and (\forall n\in\mathbb{N}:P(n)\rightarrow P(n+1))\Big]\rightarrow\forall n\in\mathbb{N}:P(n)](/images/math/1/3/6/13698cfc11b7ebb897083ddd73930f54.png)
- x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד).
נגדיר את הפרדיקט בעל שני המשתנים "x מחלק את y" ונסמן אותו באופן הנהוג 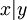 . לכן x ראשוני אם
. לכן x ראשוני אם 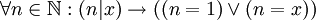
- כל מספר ראשוני הינו סכום של מספרים זוגיים.
![\forall x\in\mathbb{N}:\Big[\forall n\in\mathbb{N}: (n|x)\rightarrow ((n=1)\or(n=x))\Big]\rightarrow \Big[\exists n\in\mathbb{N}\exists k\in\mathbb{N}:2n+2k=x\Big]](/images/math/e/8/9/e89caa7ac3bb48b1dad3c95da807bd07.png)
- קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.)
"קיימים אינסוף" הוא תנאי שיש להגדיר. ההגדרה האינטואיטיבית הינה לא קיים מספר סופי של איברים כאלה, כלומר ההנחה שיש מספר סופי תוביל לשלילה. הראנו בתרגיל אחר שזה שקול לטענה לכל מספר יש מספר הגדול ממנו המקיים את התנאי, וזה מה שנצרין כאן.
![\forall n\in\mathbb{N}\exists x\in\mathbb{N}:\Big[x>n\Big]\and\Big[\forall k\in\mathbb{N}: (k|x)\rightarrow ((k=1)\or(k=x))\Big] \and \Big[\forall k\in\mathbb{N}: (k|x+2)\rightarrow ((k=1)\or(k=x+2))\Big]](/images/math/3/a/9/3a98dfc726b858886a0259a81f6ea588.png)
קבוצות
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
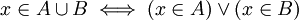
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
![x\notin A\cup B \iff \neg\Big[(x\in A) \or (x\in B)\Big]\iff (x\notin A) \and (x\notin B)](/images/math/4/2/6/4267aba5814ee2b9434827da07ed133e.png)
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
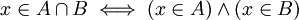
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
![x\notin A\cap B \iff \neg\Big[(x\in A) \and (x\in B)\Big]\iff (x\notin A) \or (x\notin B)](/images/math/6/8/8/688f6dab28cf8694ce41cdc64e36a144.png)
- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
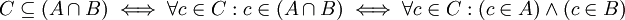
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
![\neg\Big[C\subseteq (A\cap B)\Big]\iff \neg\Big[\forall c\in C: (c\in A) \and (c\in B)\Big]\iff \exists c\in C: (c\notin A)\or (c\notin B)](/images/math/f/1/2/f12c41b86eb801b36b576ddd912d3701.png)
שקילות
הגדרה: טענות 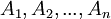 שקולות אם ((כולן אמיתיות יחד) או (כולן שקריות יחד)).
שקולות אם ((כולן אמיתיות יחד) או (כולן שקריות יחד)).
- הוכח שמספיק להוכיח את הטענות הבאות על מנת להוכיח ש
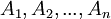 שקולות:
שקולות:
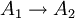 ,
,
 ,
,
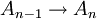 ,
,
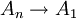
דרכי הוכחה
הוכח שהפסוקים הבאים הינם טאוטולוגיות:
(נהוג להחליף ביטויים מהצורה הזו בביטויים השקולים להם כי הם נוחים יותר להוכחה מידי פעם.)