88-101 חשיבה מתמטית קיץ תשעא/תרגילים/פתרון 2
שאלה 1
הגדרה: הגבול של הפונקציה f בנקודה x הינו L אם לכל סדרה 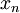 המתכנסת לx ושאבריה שונים מx מתקיים שהסדרה
המתכנסת לx ושאבריה שונים מx מתקיים שהסדרה 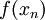 מתכנסת ל-L.
מתכנסת ל-L.
(הגדרת גבול של סדרה היא כפי שלמדנו בשיעור)
- הצרן את ההגדרה לעיל
- הצרן את השלילה להגדרה (כלומר, מתי L אינו גבול הפונקציה בנקודה x)
נסמן סדרה ממשית ב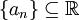 . אם כן, ההצרנה של הגדרת הגבול הינה:
. אם כן, ההצרנה של הגדרת הגבול הינה:
במילים: לכל סדרה מתקיים אם (כל איברי הסדרה שונים מ-x וגם גבול הסדרה הוא x) אז (גבול הסדרה המתקבלת מהפעלת הפונקציה על איברי הסדרה הוא L)
השלילה, היא שקיימת סדרה כך שהתנאי השני לא מתקיים אבל התנאי הראשון כן מתקיים. לכן:
יהי הפרדיקט 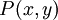 האומר אדם x צעיר יותר מאדם y. ויהי הפרדיקט
האומר אדם x צעיר יותר מאדם y. ויהי הפרדיקט 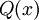 האומר שאדם x הינו שמח.
האומר שאדם x הינו שמח.
הצרן את הטענות הבאות, ואז הצרן את השלילה שלהן:
- מבין כל שלושה אנשים, הצעיר ביותר הוא שמח.
נניח כי מדובר בשלושה אנשים שונים כפי שנהוג בשפה. כמו כן, נניח שאם אדם x צעיר מאדם y אזי הם שונים (כלומר צעיר ממש). נקרא לקבוצת האנשים H עבור humans.
השלילה הינה "קיימת שלישית אנשים בה האדם הצעיר ביותר עצוב.
- מבין כל שלושה אנשים שמחים, לפחות שניים הם באותו גיל
השלילה: קיימת שלישית אנשים שמחים כך שכולם בגיל שונה.
- בכל זוג יש לפחות אדם אחד שמח.
- קיים זוג בו שני האנשים שמחים רק אם קיים זוג אחר בו שני האנשים עצובים
השלילה הינה: קיים זוג שמחים ואין זוג עצובים. אין זוג עצובים אם מכל זוג יש לפחות אחד שמח.
- יש רק אדם אחד עצוב
זהו בעצם משפט קיום וגם יחידות. השלילה היא לא קיים או לא יחיד:
- יש אדם שהוא הכי מבוגר
אנחנו נסיק מכך שיש אדם שאין אף אחד מבוגר ממנו. כלומר אם יש שני מבוגרים, אז עדיין ניתן לומר שיש אחד שהוא הכי מבוגר
השלילה: לכל אדם, יש אדם המבוגר ממנו.
- אם יש אדם שהוא הכי מבוגר, הוא שמח
נצרין את זה באופן: כל אדם שהוא הכי מבוגר, הוא גם הכי שמח.
השלילה הינה: יש אדם הכי מבוגר והוא עצוב
שאלה 2
חלק את הטענות הבאות לקבוצות שקילות. כלומר, בכל קבוצה כל הטענות צריכות להיות שקולות זו לזו. בנוסף, ציין אילו קבוצות הן שלילות של איזו קבוצה:
- יש חתול שאינו שורט ואינו נושך כאשר הוא רואה כלב
- כל החתולים, כאשר הם רואים כלב הם שורטים ונושכים
- לכל החתולים יש כלב שכאשר הם רואים אותו הם שורטים או נושכים
- יש חתול שלא משנה איזה כלב יעבור מולו, הוא ינשך או ישרוט.
- יש חתול ששורט ונושך כל פעם שהוא רואה כלב.
- לכל החתולים יש כלב שיעבור מולם והם לא ינשכו ולא ישרטו.
- יש חתול שינשוך וישרוט כאשר הוא רואה כלב כלשהו.
- יש חתול שינשוך או ישרוט כאשר הוא רואה כלב כלשהו.
- זה לא נכון שיש חתול ויש כלב כך שהחתול רואה את הכלב הוא לא נושך או לא שורט.
- יש כלב שחתול מסויים אף פעם לא שורט ולא נושך כאשר הוא עובר מולו.
- כל החתולים שורטים או נושכים כאשר הם רואים כלב.
- כל החתולים לא נושכים או לא שורטים כאשר הם רואים כלב.
- כל החתולים לא נושכים ולא שורטים כאשר הם רואים כלב.
- אין חתול שכאשר הוא רואה כלב הוא לא שורט או לא נושך.
![\forall \{a_n\}\subseteq\mathbb{R}:\Big[
\big[ (\forall n\in\mathbb{N}:a_n\neq x)
\and
(\forall\epsilon >0 \exists N_{\epsilon}\in\mathbb{N}\forall n>N_{\epsilon}:|a_n-x|<\epsilon)
\big]
\rightarrow
\big[
(\forall\epsilon >0 \exists N_{\epsilon}\in\mathbb{N}\forall n>N_{\epsilon}):|f(a_n)-L|<\epsilon)
\big]
\Big]](/images/math/5/3/2/53243d66e625a5ddf31289470760f50b.png)
![\exists\{a_n\}\subseteq\mathbb{R}:\Big[
\big[ (\forall n\in\mathbb{N}:a_n\neq x)
\and
(\forall\epsilon >0 \exists N_{\epsilon}\in\mathbb{N}\forall n>N_{\epsilon}:|a_n-x|<\epsilon)
\big]
\and
\big[
(\exists\epsilon >0 \forall N_{\epsilon}\in\mathbb{N}\exists n>N_{\epsilon}):|f(a_n)-L|\geq\epsilon)
\big]
\Big]](/images/math/8/3/9/839a2fe3979c972fc12252de8cb17cf6.png)
![\forall x,y,z\in H: ([P(x,y)]\and [P(x,z)] \and [y\neq z])\rightarrow Q(x)](/images/math/9/0/8/908631ddb277a211df36b6afdaaa6a88.png)
![\exists x,y,z\in H: ([P(x,y)]\and [P(x,z)] \and [y\neq z])\and \neg Q(x)](/images/math/3/3/1/331e10ad7d7c8dc0c1117be3835f71c2.png)
![\forall x,y,z\in H:
\Big[
(x\neq y)\and (x\neq z)\and (y\neq z) \and Q(x) \and Q(y) \and Q(z)
\Big]
\rightarrow
[
(
\neg [P(x,y)\or P(y,x)]
)
\or
(
\neg [P(x,z)\or P(z,x)]
)
\or
(
\neg [P(z,y)\or P(y,z)]
)
]](/images/math/b/a/f/bafcf277e96559b6d31f62b408137aa8.png)
![\forall x,y,z\in H:
\Big[
(x\neq y)\and (x\neq z)\and (y\neq z) \and Q(x) \and Q(y) \and Q(z)
\Big]
\and
[
(
[P(x,y)\or P(y,x)]
)
\and
(
[P(x,z)\or P(z,x)]
)
\and
(
[P(z,y)\or P(y,z)]
)
]](/images/math/9/0/2/902c5ec32e39bb10f750f13ad3034794.png)
![\forall x,y\in H: (x\neq y) \rightarrow [Q(x)\or Q(y)]](/images/math/2/7/f/27ff68c4bb5288fe9c449b9cdfce065b.png)
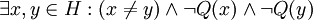
![[\exists x,y\in H: (x\neq y \and Q(x) \and Q(y)] \rightarrow [\exists x,y\in H: (x\neq y) \and \neg Q(x) \and \neg Q(y)]](/images/math/0/7/2/072d19d88ef67e9881cbac0a4b951f6e.png)
![[\exists x,y\in H: (x\neq y \and Q(x) \and Q(y)] \and[\forall x,y\in H: (x\neq y)\rightarrow [Q(x) \or Q(y)]]](/images/math/3/b/7/3b7b20a655b43b70d7ed73668b7a4e7f.png)
![\exists x\in H: [(\neg Q(x))\and (\forall y\in H: (y\neq x)\rightarrow Q(y)) ]](/images/math/b/3/d/b3db7613bb6258a119f7319f3e49c7ba.png)
![\forall x\in H: Q(x)\or [\exists y\in H: (y\neq x) \and \neg Q(y)]](/images/math/d/3/c/d3c584691ccc6aeb636555b3c5515e6e.png)
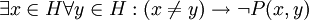
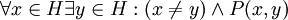
![\forall x\in H :[\forall y\in H: (x\neq y) \rightarrow \neg P(x,y)] \rightarrow Q(x)]](/images/math/d/9/0/d902e89f2556c401b2a7e1c7201365f4.png)
![\exists x\in H: [\forall y\in H: (x\neq y) \rightarrow \neg P(x,y)] \and \neg Q(x)]](/images/math/9/d/0/9d0652419d3a2c4f7ad4e4fba799bfe7.png)