הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/11"
(←תכונות של הדטרמיננטה) |
(←תרגיל) |
||
| שורה 67: | שורה 67: | ||
תהי <math>B\in F^{3\times 3}</math> עם דטרמיננטה <math>|B|=-1</math>. מצא את <math>|2B|</math>. | תהי <math>B\in F^{3\times 3}</math> עם דטרמיננטה <math>|B|=-1</math>. מצא את <math>|2B|</math>. | ||
| − | + | '''פתרון''' | |
<math>|2B|=|2I\cdot B|=|\pmatrix{2&0&0\\ 0&2&0\\ 0&0&2}|\cdot |B|=2^3 \cdot (-1)</math> | <math>|2B|=|2I\cdot B|=|\pmatrix{2&0&0\\ 0&2&0\\ 0&0&2}|\cdot |B|=2^3 \cdot (-1)</math> | ||
'''בהכללה:''' <math>|\alpha A|=\alpha^n |A|</math>. | '''בהכללה:''' <math>|\alpha A|=\alpha^n |A|</math>. | ||
גרסה מ־07:18, 3 באוגוסט 2016
תוכן עניינים
דטרמיננטות
הגדרה הדטרמיננטה של מטריצה ריבועית 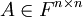 היא סקלר
היא סקלר 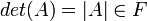 המחושב מסכומים של מכפלות של אברי המטריצה.
המחושב מסכומים של מכפלות של אברי המטריצה.
חישוב דטרמיננטה של מטריצות קטנות
- הדטרמיננטה של מטריצה מסדר 1
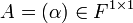 היא הערך היחיד במטריצה
היא הערך היחיד במטריצה 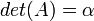 .
.
- הדטרמיננטה של מטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{a&b\\ c&d} \in F^{2\times 2}
היא.
למשל: עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): det\pmatrix{1&2\\ 3&4} = 1\cdot 4-2\cdot 3=-2 .
חישוב לפי נוסחת לפלס (מינורים)
סימון עבור מטריצה 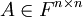 נסמן ב
נסמן ב 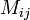 את המטריצה מגודל
את המטריצה מגודל 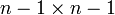 המתקבלת מ
המתקבלת מ ע"י מחיקת השורה ה
ע"י מחיקת השורה ה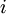 והעמודה ה
והעמודה ה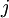 . זה נקרא המינור ה
. זה נקרא המינור ה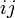 של המטריצה.
של המטריצה.
דוגמא: עבור עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
למשל
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{12}=\pmatrix{4&6\\ 7&9}
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{23}=\pmatrix{1&2\\ 7&8}
אפשר למצוא את הדטרמיננטה בעזרת הדטרמיננטות של המינורים (לפי שורה או לפי עמודה), וכך באינדוקציה למצוא דטורמיננטה של כל מטריצה.
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי השורה ה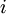 :
:
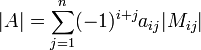
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי העמודה ה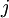 :
:
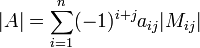
לדוגמא: עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
נפתח לפי השורה הראשונה:
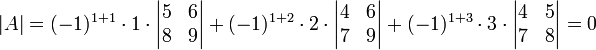
נפתח גם לפי העמודה השנייה:
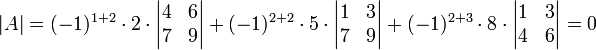
תכונות של הדטרמיננטה
1. כפליות 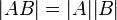 .
.
2. בפרט 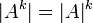 .
.
3. 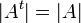 .
.
4. אם המטריצה משולשית אז הדטרמיננטה= מכפלת אברי האלכסון (להדגים?).
5. אם  הפיכה אז
הפיכה אז 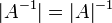 .
.
6.  הפיכה אם"ם
הפיכה אם"ם 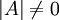 .
.
למשל המטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
איננה הפיכה כי חישבנו שהדטרמיננטה היא אפס.
שימו לב שאין בהכרח קשר בין 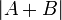 לבין
לבין 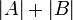 . (דוגמא?)
. (דוגמא?)
תרגיל
נתונות מטריצות 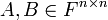 כך ש
כך ש 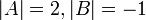 . חשבו את
. חשבו את 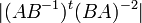 .
.
פתרון
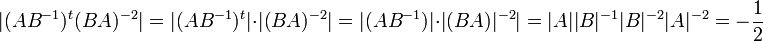
תרגיל
תהי 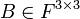 עם דטרמיננטה
עם דטרמיננטה 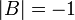 . מצא את
. מצא את 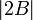 .
.
פתרון
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): |2B|=|2I\cdot B|=|\pmatrix{2&0&0\\ 0&2&0\\ 0&0&2}|\cdot |B|=2^3 \cdot (-1)
בהכללה: 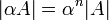 .
.