הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/11"
(←תרגיל) |
(←תכונות של הדטרמיננטה) |
||
| שורה 88: | שורה 88: | ||
3. נעביר אגפים <math>AB=-BA</math> ונקח דטרמיננטה <math>|A||B|=(-1)^n|B||A|</math>. נתון ש<math>n</math> אי-זוגי ולכן <math>|A||B|=-|A||B|</math>. | 3. נעביר אגפים <math>AB=-BA</math> ונקח דטרמיננטה <math>|A||B|=(-1)^n|B||A|</math>. נתון ש<math>n</math> אי-זוגי ולכן <math>|A||B|=-|A||B|</math>. | ||
זה מכריח ש<math>|A||B|=0</math> ולכן או ש <math>|A|=0</math>ואז <math>A</math>לא הפיכה, או ש<math>|B|=0</math> ואז <math>B</math>לא הפיכה. | זה מכריח ש<math>|A||B|=0</math> ולכן או ש <math>|A|=0</math>ואז <math>A</math>לא הפיכה, או ש<math>|B|=0</math> ואז <math>B</math>לא הפיכה. | ||
| + | |||
| + | |||
| + | ===תרגיל=== | ||
| + | תהי <math>A</math>מטריצה ממשית אנטי-סימטרית מסדר אי-זוגי. הוכיחו כי היא איננה הפיכה. | ||
| + | |||
| + | '''פתרון''' | ||
| + | לפי הנתון <math>A^t=-A</math> ולכן <math>|A|=|A^t|=|-A|=(-1)^n|A|</math> מה שגורר <math>|A|=0</math>. | ||
==שיטת הדירוג== | ==שיטת הדירוג== | ||
גרסה מ־18:57, 3 באוגוסט 2016
תוכן עניינים
דטרמיננטות
הגדרה הדטרמיננטה של מטריצה ריבועית 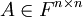 היא סקלר
היא סקלר 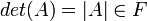 המחושב מסכומים של מכפלות של אברי המטריצה.
המחושב מסכומים של מכפלות של אברי המטריצה.
חישוב דטרמיננטה של מטריצות קטנות
- הדטרמיננטה של מטריצה מסדר 1
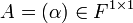 היא הערך היחיד במטריצה
היא הערך היחיד במטריצה 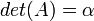 .
.
- הדטרמיננטה של מטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{a&b\\ c&d} \in F^{2\times 2}
היא.
למשל: עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): det\pmatrix{1&2\\ 3&4} = 1\cdot 4-2\cdot 3=-2 .
חישוב לפי נוסחת לפלס (מינורים)
סימון עבור מטריצה 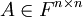 נסמן ב
נסמן ב 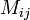 את המטריצה מגודל
את המטריצה מגודל 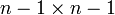 המתקבלת מ
המתקבלת מ ע"י מחיקת השורה ה
ע"י מחיקת השורה ה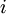 והעמודה ה
והעמודה ה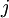 . זה נקרא המינור ה
. זה נקרא המינור ה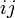 של המטריצה.
של המטריצה.
דוגמא: עבור עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9} למשל עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{12}=\pmatrix{4&6\\ 7&9}
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{23}=\pmatrix{1&2\\ 7&8}
אפשר למצוא את הדטרמיננטה בעזרת הדטרמיננטות של המינורים (לפי שורה או לפי עמודה), וכך באינדוקציה למצוא דטורמיננטה של כל מטריצה.
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי השורה ה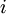 :
:
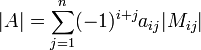
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי העמודה ה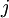 :
:
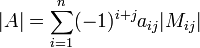
לדוגמא:
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
נפתח לפי השורה הראשונה:
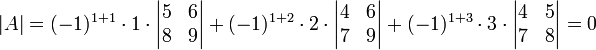
נפתח גם לפי העמודה השנייה:
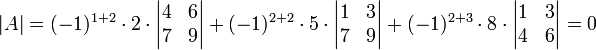
תכונות של הדטרמיננטה
1. כפליות 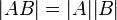 .
.
2. בפרט 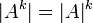 .
.
3. 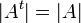 .
.
4. אם המטריצה משולשית אז הדטרמיננטה= מכפלת אברי האלכסון (להדגים?).
5. אם  הפיכה אז
הפיכה אז 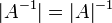 .
.
6.  הפיכה אם"ם
הפיכה אם"ם 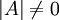 .
.
למשל המטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
איננה הפיכה כי חישבנו שהדטרמיננטה היא אפס.
שימו לב שאין בהכרח קשר בין 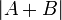 לבין
לבין 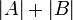 . (דוגמא?)
. (דוגמא?)
תרגיל
נתונות מטריצות 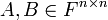 כך ש
כך ש 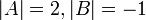 . חשבו את
. חשבו את 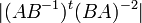 .
.
פתרון
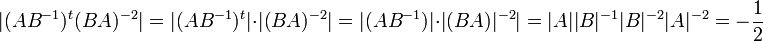
תרגיל
תהי 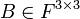 עם דטרמיננטה
עם דטרמיננטה 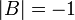 . מצא את
. מצא את 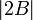 .
.
פתרון
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): |2B|=|2I\cdot B|=|\pmatrix{2&0&0\\ 0&2&0\\ 0&0&2}|\cdot |B|=2^3 \cdot (-1)
בהכללה: 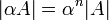 .
.
תרגיל
1. תהי  מטריצה ממשית והפיכה מסדר
מטריצה ממשית והפיכה מסדר  המקיימת
המקיימת 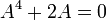 . חשבו את
. חשבו את 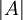 .
.
2. נניח  מקיימת
מקיימת 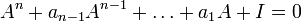 , הוכיחו כי היא הפיכה.
, הוכיחו כי היא הפיכה.
3.תהיינה 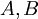 ריבועיות מסדר
ריבועיות מסדר  אי-זוגי מעל שדה ממאפיין שונה מ2. נתון ש
אי-זוגי מעל שדה ממאפיין שונה מ2. נתון ש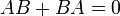 , הוכיחו כי אחת מהמטריצות איננה הפיכה.
, הוכיחו כי אחת מהמטריצות איננה הפיכה.
פתרון:
1. נעביר אגפים ונקבל 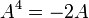 , נקח דטרמיננטה
, נקח דטרמיננטה 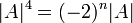 ולכן
ולכן 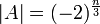 .
.
2. נעביר אגפים ונסדר 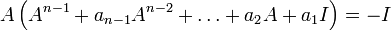 , נקח דטרמיננטה
, נקח דטרמיננטה 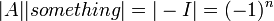 . בפרט,
. בפרט, 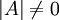 ולכן
ולכן  הפיכה.
הפיכה.
3. נעביר אגפים 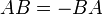 ונקח דטרמיננטה
ונקח דטרמיננטה 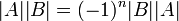 . נתון ש
. נתון ש אי-זוגי ולכן
אי-זוגי ולכן 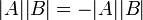 .
זה מכריח ש
.
זה מכריח ש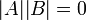 ולכן או ש
ולכן או ש 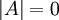 ואז
ואז  לא הפיכה, או ש
לא הפיכה, או ש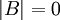 ואז
ואז  לא הפיכה.
לא הפיכה.
תרגיל
תהי  מטריצה ממשית אנטי-סימטרית מסדר אי-זוגי. הוכיחו כי היא איננה הפיכה.
מטריצה ממשית אנטי-סימטרית מסדר אי-זוגי. הוכיחו כי היא איננה הפיכה.
פתרון
לפי הנתון 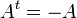 ולכן
ולכן 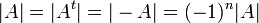 מה שגורר
מה שגורר 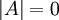 .
.
שיטת הדירוג
טענה תהי  מטריצה המתקבלת ממטריצה
מטריצה המתקבלת ממטריצה  ע" פעולת שורה, אזי:
ע" פעולת שורה, אזי:
1. אם  התקבלה ע"י כפל של אחת השורות ב
התקבלה ע"י כפל של אחת השורות ב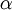 אזי
אזי 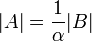 .
.
2. אם  התקבלה ע"י החלפת שתי שורות אזי
התקבלה ע"י החלפת שתי שורות אזי 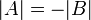 .
.
3. אם  התקבלה ע"י הוספת כפולה של שורה אחת לשורה אחרת אזי
התקבלה ע"י הוספת כפולה של שורה אחת לשורה אחרת אזי 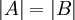 .
.
אם כן, נוכל לחשב דטרמיננטה ע"י דירוג המטריצה עד לצורה משולשית עליונה, ולעקוב אחר השינויים בדטרמיננטה.
דוגמא
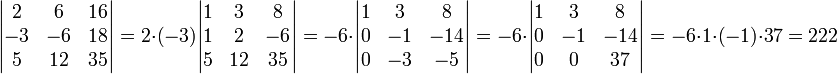
דוגמא
חשב את
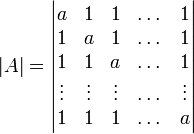
פתרון
ראשית נסכום את כל השורות לשורה הראשונה ונקבל 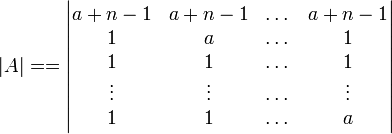 נחלק את השורה הראשונה ב
נחלק את השורה הראשונה ב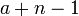 ונקבל:
ונקבל:
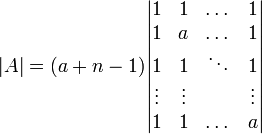
כעת נחסר מכל שורה את השורה הראשונה ונקבל
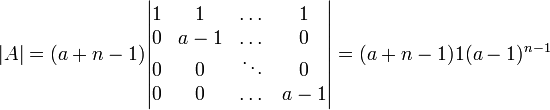
הערה מכיוון ו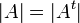 מותר בחישוב הדטרמיננטה לעשות גם פעולות עמודה אלמנטריות, השינוי בדטרמיננטה הוא דומה.
מותר בחישוב הדטרמיננטה לעשות גם פעולות עמודה אלמנטריות, השינוי בדטרמיננטה הוא דומה.
=תרגיל
נתון ש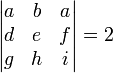 . חשבו את
. חשבו את 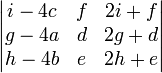 .
.
פתרון: נשתמש בפעולות שורה ועמודה ונעקוב אחר השינויים בדטרמיננטה:
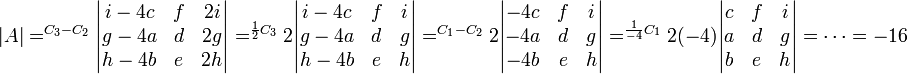
המטריצה הנילוות (המצורפת)
הגדרה תהי 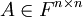 , המטריצה נילווית שלה היא המטריצה
, המטריצה נילווית שלה היא המטריצה 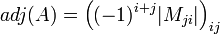 .
.
(שימו לב להחלפה בין 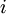 ו עיבוד הנוסחה נכשל (שגיאת לקסינג): j</math !) דוגמא ==המשפט המרכזי== <math>A(adjA)=(adjA)A=|A|I
ו עיבוד הנוסחה נכשל (שגיאת לקסינג): j</math !) דוגמא ==המשפט המרכזי== <math>A(adjA)=(adjA)A=|A|I
תוצאה: אם  הפיכה אז
הפיכה אז 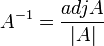 .
.
תרגיל
תהי 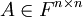 מטריצה.
1. הוכח כי
מטריצה.
1. הוכח כי 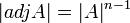 .
2. נניח כי המטריצה הפיכה, חשבו את
.
2. נניח כי המטריצה הפיכה, חשבו את 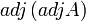 .
.
פתרון
1. ראשית נניח כי 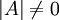 , אזי נפעיל דטרמיננטה על שני האגפים:
, אזי נפעיל דטרמיננטה על שני האגפים: 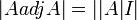 ונקבל
ונקבל 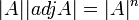 נחלק בדטרמיננטה ואז
נחלק בדטרמיננטה ואז 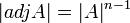 כדרוש.
כדרוש.
כעת נניח 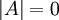 וצריך להוכיח כי
וצריך להוכיח כי 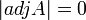 .
לפי המשפט
.
לפי המשפט 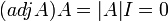
אם 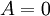 אז ברור ש
אז ברור ש 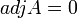 לפי ההגדרה.
אחרת, יש איזשהי עמודה של
לפי ההגדרה.
אחרת, יש איזשהי עמודה של  שהיא לא אפס,
שהיא לא אפס, 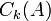 . ואז
. ואז 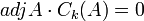 מה שאומר ש
מה שאומר ש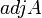 לא הפיכה ואז
לא הפיכה ואז 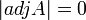 .
.
2. נשתמש במשפט עבור המטריצה 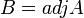 , אזי
, אזי 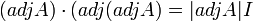 . ולפי הסעיף הקודם נקבל ש
. ולפי הסעיף הקודם נקבל ש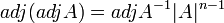 . ומכיוון ו
. ומכיוון ו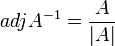 אז
אז 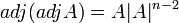 .
.
תרגיל
תהי 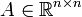 המקיימת
המקיימת 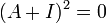 .
.
א. הוכיחו כי  הפיכה.
הפיכה.
ב. הביעו את 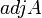 באמצעות
באמצעות 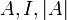 בלבד.
בלבד.
פתרון:
א. נפתח ונקבל 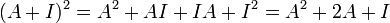 נעביר אגפים ונקבל
נעביר אגפים ונקבל 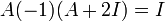 ולכן
ולכן  הפיכה.
הפיכה.
ב.לפי המשפט 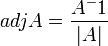 ולכן בעצם נשאר למצוא ביטוי ל
ולכן בעצם נשאר למצוא ביטוי ל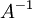 .
לפי הסעיף הקודם
.
לפי הסעיף הקודם 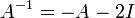 ולכן
ולכן 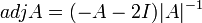 .
.
תרגיל
תהי 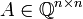 ונתון שהיא הפיכה ב
ונתון שהיא הפיכה ב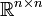 (כלומר שיש מטריצה ממשית
(כלומר שיש מטריצה ממשית  כך ש
כך ש 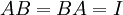 ). הוכיחו כי היא הפיכה ב
). הוכיחו כי היא הפיכה ב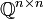 .
.
פתרון:
מכיוון שמטריצה הפיכה היא יחידה, לא יתכן שב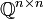 יש מטריצה הופכית אחרת. כך שבעצם יש להראות ש
יש מטריצה הופכית אחרת. כך שבעצם יש להראות ש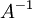 הממשית היא בעצם עם איברים ב
הממשית היא בעצם עם איברים ב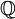 .
.
לפי המשפט 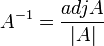 .
.
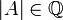 כי הדטרמיננטה זה סכומים של מכפלות של איברי
כי הדטרמיננטה זה סכומים של מכפלות של איברי  שהם רציונליים.
שהם רציונליים.
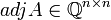 כי האיברים הם
כי האיברים הם 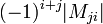 שהם גם רציונלים (כמו קודם).
סה"כ קיבלנו
שהם גם רציונלים (כמו קודם).
סה"כ קיבלנו 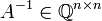 .
.
דטרמיננטות של העתקות לינאריות
טענה אם  מטריצה ריבועית ו
מטריצה ריבועית ו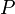 מטריצה הפיכה, אזי
מטריצה הפיכה, אזי 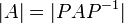 .
.
(הוכחה: 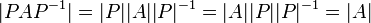 ).
).
ראינו בעבר שאם 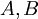 הן מטריצות מייצגות של אותה העתקה לינארית
הן מטריצות מייצגות של אותה העתקה לינארית 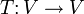 אזי יש מטריצה הפיכה
אזי יש מטריצה הפיכה 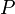 (למעשה מטריצת מעבר בסיסים) כך ש
(למעשה מטריצת מעבר בסיסים) כך ש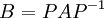 . לאור הטענה הקודמת רואים שלא משנה איך נחשב את המטריצה המייצגת, הדטרמיננטה תישאר אותו דבר. ולכן אפשר להגדיר...
. לאור הטענה הקודמת רואים שלא משנה איך נחשב את המטריצה המייצגת, הדטרמיננטה תישאר אותו דבר. ולכן אפשר להגדיר...
הגדרה הדטרמיננטה של העתקה לינארית 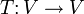 היא הדטרמיננטה של מטריצה מייצגת (כלשהי).
היא הדטרמיננטה של מטריצה מייצגת (כלשהי).
טענה שימושית העתקה 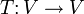 היא הפיכה אם"ם הדטרמיננטה שלה שונה מאפס.
היא הפיכה אם"ם הדטרמיננטה שלה שונה מאפס.
עוד טענה שימושית תהיינה 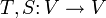 הע"ל. אזי
הע"ל. אזי 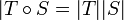 .
.