שיעור שני
אלגברת מטריצות
הגדרה: האיבר הij בכפל AB מוגדר להיות ![[AB]_{ij}=\sum_{k=1}^na_{ik}b_{kj}](/images/math/7/7/1/771cfd1848c4559c8c4f91240a6f893e.png)
ניתן לבצע את הכפל AB אם"ם מספר העמודות של A זהה למספר השורות של B (ונקרא n בנוסחא למעלה). אמנם פעולת הכפל נראית משונה, אך נראה בהמשך כי היא משמעותית למדי.
תרגיל 3.4 ג-ז
נתונה מערכת של m משוואות בn נעלמים: Ax=b (זה זמן טוב לראות דוגמא ראשונה של המשמעות של כפל מטריצות). נסמן ב 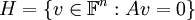 את קבוצת הפתרונות של המערכת ההומוגנית המתאימה, וב
את קבוצת הפתרונות של המערכת ההומוגנית המתאימה, וב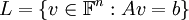 את קבוצת הפתרונות של המערכת הלא-הומוגנית. הוכח את הטענות הבאות:
את קבוצת הפתרונות של המערכת הלא-הומוגנית. הוכח את הטענות הבאות:
ג
אם L אינה קבוצה ריקה, אזי כמות הפתרונות בH שווה לכמות הפתרונות בL
פתרון
נוכיח את הטענה על ידי יצירת פונקציה חח"ע ועל בין H לבין L. יהיה 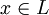 כלשהו (הקיים לפי הנתון). נביט בהעתקה
כלשהו (הקיים לפי הנתון). נביט בהעתקה 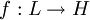 המוגדרת ע"י
המוגדרת ע"י 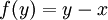 . יש להוכיח כי זו אכן פונקציה מוגדרת היטב (כלומר, y-x הוא פתרון של המערכת ההומוגנית) ואז יש להראות כי זה פונקציה חח"ע ועל.
. יש להוכיח כי זו אכן פונקציה מוגדרת היטב (כלומר, y-x הוא פתרון של המערכת ההומוגנית) ואז יש להראות כי זה פונקציה חח"ע ועל.
דבר ראשון, נבדוק האם y-x הינו פתרון של המערכת ההומוגנית. 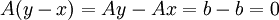 כפי שרצינו.
כפי שרצינו.
דבר שני, נניח כי 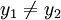 לכן ברור ש
לכן ברור ש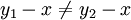 (במילים, לכל שני פתרונות שונים מL מתאימים שני פתרונות שונים בH).
(במילים, לכל שני פתרונות שונים מL מתאימים שני פתרונות שונים בH).
דבר שלישי, נראה כי לכל פתרון y בH, יש פתרון בL הנשלח אליו. פתרון זה הינו כמובן y+x שכן 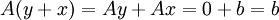 .
.
לכן סה"כ הראנו כי לכל פתרון בL מתאים פתרון יחיד בH ולכן הקבוצות הנ"ל הן באותו גודל.
ד
מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש פתרון יחיד למערכת ההומוגנית
פתרון
נביט במטריצה 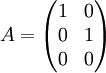 ובוקטור הפתרונות
ובוקטור הפתרונות 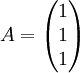 . במערכת Ax=b ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש פתרון יחיד (0,0).
. במערכת Ax=b ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש פתרון יחיד (0,0).
ה
מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש אינסוף פתרונות למערכת ההומוגנית
פתרון
נביט במטריצה 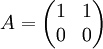 ובוקטור הפתרונות
ובוקטור הפתרונות 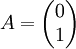 . במערכת Ax=b מעל הממשיים ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש אינסוף פתרונות.
. במערכת Ax=b מעל הממשיים ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש אינסוף פתרונות.
ו
מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש 7 פתרונות למערכת ההומוגנית
פתרון
נביט במטריצה 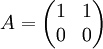 ובוקטור הפתרונות
ובוקטור הפתרונות 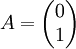 . במערכת Ax=b מעל השדה
. במערכת Ax=b מעל השדה 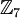 ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש 7 פתרונות מכיוון שיש משתנה חופשי יחיד.
ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש 7 פתרונות מכיוון שיש משתנה חופשי יחיד.
ז
נתון שמספר המשוואות זהה למספר הנעלמים. עוד נתון שאין פתרונות למערכת הלא-הומוגנית. מה ניתן לומר על מספר הפתרונות של המערכת ההומוגנית?
פתרון
נדרג את המטריצה A. מכיוון שאין פתרונות למערכת הלא-הומוגנית, חייבת להיות בצורה המדורגת של A שורת אפסים (אחרת יש אותו מספר של איברים מובילים ושל משתנים ולכן אין משתנים חופשיים וכל משתנה נקבע באופן יחיד על ידי וקטור הפתרונות). מכיוון שיש שורת אפסים בצורה המדורגת, יש משתנה חופשי ולכן יש יותר מפתרון אחד למערכת ההומוגנית (מספר הפתרונות הוא מספר האיברים בשדה בחזקה מספר המשתנים החופשיים, ובכל שדה יש לפחות שני איברים שונים).
סוגים שונים של כפל מטריצות
בנוסף לכפל הרגיל, חשוב מאד לדעת גם כפל שורה שורה וכפל עמודה עמודה:
נביט במטריצה 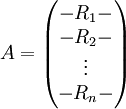 ששורותיה הן
ששורותיה הן 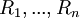 , ונביט בוקטור השורה
, ונביט בוקטור השורה 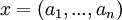 . מתקיים ש
. מתקיים ש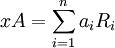 . במילים - הכפל של השורה x במטריצה A הינה סכום של שורות A כפול הקבועים מהשורה x. נובע בקלות שהשורה ה-j בכפל AB הינה סכום שורות B כפול הקבועים המתאימים מהשורה ה-j של A.
. במילים - הכפל של השורה x במטריצה A הינה סכום של שורות A כפול הקבועים מהשורה x. נובע בקלות שהשורה ה-j בכפל AB הינה סכום שורות B כפול הקבועים המתאימים מהשורה ה-j של A.
באופן דומה, נביט במטריצה 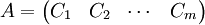 שעמותודיה הן
שעמותודיה הן 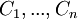 , ונביט בוקטור העמודה
, ונביט בוקטור העמודה 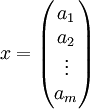 . מתקיים ש
. מתקיים ש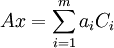 . במילים - הכפל של מטריצה בעמודה שווה לסכום עמודות המטריצה כפול הקבועים מהעמודה. נובע בקלות שהעמודה ה-j בכפל AB שווה לסכום עמודות A כפול הקבועים המתאימים מהעמודה ה-j של B. שימו לב שמערכת משוואות הינה מקרה פרטי של כפל עמודה-עמודה.
. במילים - הכפל של מטריצה בעמודה שווה לסכום עמודות המטריצה כפול הקבועים מהעמודה. נובע בקלות שהעמודה ה-j בכפל AB שווה לסכום עמודות A כפול הקבועים המתאימים מהעמודה ה-j של B. שימו לב שמערכת משוואות הינה מקרה פרטי של כפל עמודה-עמודה.
מטריצת בלוקים. מטריצה בלוקים הינה מטריצה הבנוייה ממספר מטריצות קטנות יותר (המכונות בלוקים). לדוגמא, ניקח את המטריצה 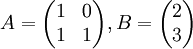 . אזי מטריצת הבלוקים מוגדרת להיות
. אזי מטריצת הבלוקים מוגדרת להיות 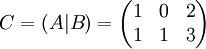
משפט: לכל שלשת מטריצות A,B,C כך שהכפל מוגדר, מתקיים ש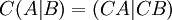 כלומר כפל C במטריצת הבלוקים, הוא מטריצה הבלוקים המורכבת מהכפל של C בכל בלוק.
כלומר כפל C במטריצת הבלוקים, הוא מטריצה הבלוקים המורכבת מהכפל של C בכל בלוק.
הוכחה: נובע בקלות מכפל עמודה-עמודה המוזכר לעיל.
תרגיל 3.7
תהא מערכת Ax=b, יהיה v פתרון למערכת הלא-הומוגנית ו-w פתרון למערכת ההומוגנית Ax=0. נגדיר 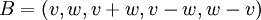 חשב את AB
חשב את AB
פתרון
לפי כפל מטריצות בלוקים קל לוודא ש 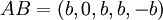
שחלוף וסמטריות
הגדרה: תהי מטריצה A. אזי המטריצה המשוחלפת 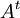 מוגדרת ע"י
מוגדרת ע"י ![[A^t]_{ij}=[A]_{ji}](/images/math/2/0/9/209f15d7650597a91ab1f9ed77aa8fab.png) . כלומר, האיבר בשורה ה-i והעמודה ה-j של המטריצה המשוחלפת הוא האיבר בשורה ה-j והעמודה ה-i של המטריצה המקורית - הפכנו את השורות לעמודות, ואת העמודות לשורות.
. כלומר, האיבר בשורה ה-i והעמודה ה-j של המטריצה המשוחלפת הוא האיבר בשורה ה-j והעמודה ה-i של המטריצה המקורית - הפכנו את השורות לעמודות, ואת העמודות לשורות.
דוגמא: אם 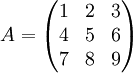 אזי
אזי 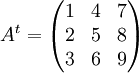
הגדרה: מטריצה נקראת סמטרית אם היא שווה למשוחלפת של עצמה 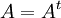 (השורות והעמודות שלה זהות). מטריצה נקראת אנטי-סימטרית אם
(השורות והעמודות שלה זהות). מטריצה נקראת אנטי-סימטרית אם 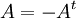
תכונות:
- לכל שתי מטריצות A,B כך שהכפל מוגדר ש
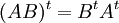 .
. 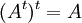
- לכל שתי מטריצות A,B באותו גודל מתקיים
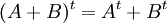
- לכל מטריצה A, ולכל קבוע מהשדה c מתקיים ש
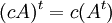
תרגיל 4.4
א. הוכח שלכל מטריצה 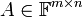 המטריצה
המטריצה 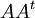 הינה סימטרית.
הינה סימטרית.
ב. הוכח שלכל מטריצה ריבועית A מתקיים שהמטריצה 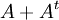 סימטרית, ואילו המטריצה
סימטרית, ואילו המטריצה 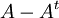 אנטי סימטרית.
אנטי סימטרית.
פתרון
א. נסמן 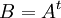 . לפי התכונות לעיל קל לראות ש
. לפי התכונות לעיל קל לראות ש 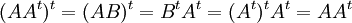 והוכחנו שהמטריצה סימטרית.
והוכחנו שהמטריצה סימטרית.
ב. 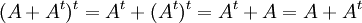 (הרי חיבור מטריצות הוא חילופי). כמו כן,
(הרי חיבור מטריצות הוא חילופי). כמו כן, 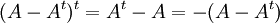 כפי שרצינו.
כפי שרצינו.