הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/6"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏קואורדינטות)
(←‏קואורדינטות)
שורה 1: שורה 1:
 
==קואורדינטות==
 
==קואורדינטות==
−
נסביר את כל המושגים תוך כדי שימוש בדוגמא קבועה: <math>V=\mathbb{R}^2, S_{\mathbb{R}^2}=\{(1,0),(0,1)\},B=\{(1,1),(1,-1)\}</math>, מתקיים ששתי הקבוצות מהוות בסיס למרחב V.
+
נסביר את כל המושגים תוך כדי שימוש בדוגמא קבועה: <math>V=\mathbb{R}^2, S_{\mathbb{R}^2}=\{(1,0),(0,1)\},D=\{(1,1),(1,-1)\}</math>, מתקיים ששתי הקבוצות מהוות בסיס למרחב V.
  
 
משפט: יהא V מ"ו מעל שדה F, יהי <math>B=\{v_1,...,v_n\}</math> בסיס ל-V ויהי <math>v\in V</math> וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים <math>v=a_1v_1+...+a_nv_n=b_1v_1+...+b_nv_n</math> אזי בהכרח <math>\forall i:a_i=b_i</math>. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים <math>a_i-b_i</math>.)
 
משפט: יהא V מ"ו מעל שדה F, יהי <math>B=\{v_1,...,v_n\}</math> בסיס ל-V ויהי <math>v\in V</math> וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים <math>v=a_1v_1+...+a_nv_n=b_1v_1+...+b_nv_n</math> אזי בהכרח <math>\forall i:a_i=b_i</math>. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים <math>a_i-b_i</math>.)
שורה 8: שורה 8:
  
 
'''חשוב לזכור''' <math>[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}</math> אם"ם <math>v=a_1v_1+...+a_nv_n</math>
 
'''חשוב לזכור''' <math>[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}</math> אם"ם <math>v=a_1v_1+...+a_nv_n</math>
 +
 +
תרגיל קל אבל חשוב הוא להראות שלכל בסיס B מתקיים ש <math>v=0</math> אם"ם <math>[v]_B=0</math>.
 +
 +
 +
הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש '''בסיסים סטנדרטיים'''. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם:
 +
 +
 +
{| border="1" align="center" style="text-align:center;"
 +
|מרחב וקטורי
 +
|בסיס סטנדרטי
 +
|-
 +
|<math>\mathbb{F}^n</math>
 +
|<math>(1,0,...,0),(0,1,0,...,0),...,(0,...,0,1)</math>
 +
|-
 +
|<math>\mathbb{F}^{m\times n}</math>
 +
|<math>
 +
\begin{pmatrix}1 & 0 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix},
 +
\begin{pmatrix}0 & 1 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix},...,
 +
\begin{pmatrix}0 & \cdots & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0 & 1 \end{pmatrix}
 +
</math>
 +
|-
 +
|<math>\mathbb{F}_n[x]</math>
 +
|<math>1,x,x^2,...,x^n</math>
 +
|-
 +
|}
 +
 +
===תרגיל===
 +
יהא V מ"ו ויהי B בסיס לו. יהיו <math>u_1,...,u_k\in V</math> וקטורים כלשהם. הוכח:
 +
*<math>u_1,...,u_k</math> בת"ל אם"ם <math>[u_1]_B,...,[u_k]_B</math> בת"ל
 +
*<math>w\in span\{u_1,...,u_k\}</math> אם"ם <math>w\in span\{[u_1]_B,...,[u_k]_B\}</math>
 +
 +
נוכיח תרגיל זה בהמשך, לאחר שנלמד על העתקות לינאריות. כעת נניח שהוא נכון ונתרכז בכלי החישובי המשמעותי שקיבלנו; כל בדיקה/חישוב של תלות לינארית או פרישה בכל מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח <math>\mathbb{F}^n</math>.
 +
 +
===דוגמא===
 +
האם הפולינומים <math>1+x^2,</math>

גרסה מ־20:50, 29 ביולי 2011

קואורדינטות

נסביר את כל המושגים תוך כדי שימוש בדוגמא קבועה: 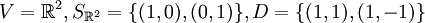V=\mathbb{R}^2, S_{\mathbb{R}^2}=\{(1,0),(0,1)\},D=\{(1,1),(1,-1)\}, מתקיים ששתי הקבוצות מהוות בסיס למרחב V.

משפט: יהא V מ"ו מעל שדה F, יהי 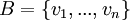B=\{v_1,...,v_n\} בסיס ל-V ויהי 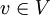v\in V וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים 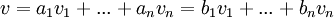v=a_1v_1+...+a_nv_n=b_1v_1+...+b_nv_n אזי בהכרח 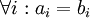\forall i:a_i=b_i. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים a_i-b_i.)

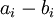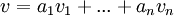הגדרה: יהיו V,B וv כמו במשפט. אזי וקטור הקואורדינטות של v לפי בסיס B, מסומן [v]_B\in\mathbb{F}^n מוגדר להיות [v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix} כאשר v=a_1v_1+...+a_nv_n ההצגה הלינארית היחידה הקיימת לפי המשפט.


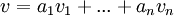
חשוב לזכור [v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix} אם"ם v=a_1v_1+...+a_nv_n

תרגיל קל אבל חשוב הוא להראות שלכל בסיס B מתקיים ש 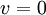v=0 אם"ם [v]_B=0.


הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש בסיסים סטנדרטיים. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם:


מרחב וקטורי בסיס סטנדרטי
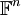
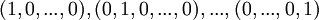
\mathbb{F}^n (1,0,...,0),(0,1,0,...,0),...,(0,...,0,1)
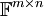
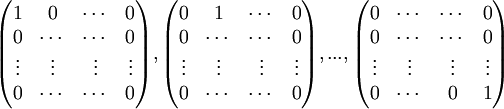
\mathbb{F}^{m\times n} \begin{pmatrix}1 & 0 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix}, \begin{pmatrix}0 & 1 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix},..., \begin{pmatrix}0 & \cdots & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0 & 1 \end{pmatrix}
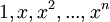
\mathbb{F}_n[x] 1,x,x^2,...,x^n

תרגיל

יהא V מ"ו ויהי B בסיס לו. יהיו 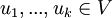u_1,...,u_k\in V וקטורים כלשהם. הוכח:

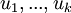  • u_1,...,u_k בת"ל אם"ם [u_1]_B,...,[u_k]_B בת"ל
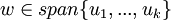  • w\in span\{u_1,...,u_k\} אם"ם w\in span\{[u_1]_B,...,[u_k]_B\}

נוכיח תרגיל זה בהמשך, לאחר שנלמד על העתקות לינאריות. כעת נניח שהוא נכון ונתרכז בכלי החישובי המשמעותי שקיבלנו; כל בדיקה/חישוב של תלות לינארית או פרישה בכל מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח 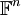\mathbb{F}^n.

דוגמא

האם הפולינומים 1+x^2,

מקור: https://math-wiki.com/index.php?title=88-112_לינארית_1_תיכוניסטים_קיץ_תשעא/מערך_תרגול/6&oldid=11896