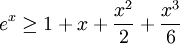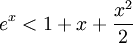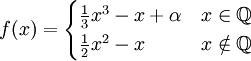הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/דמה1"
מתוך Math-Wiki
(←4) |
(←ב) |
||
| שורה 35: | שורה 35: | ||
===ב=== | ===ב=== | ||
| + | מצא לאילו ערכי <math>\alpha</math> ובאילו נקודות הפונקציה הבאה גזירה: | ||
| + | ::<math>f(x)=\begin{cases} \frac{1}{3}x^3-x+\alpha&x\in\mathbb{Q}\\\frac{1}{2}x^2-x&x\notin\mathbb{Q}\end{cases}</math> | ||
| + | |||
| + | ==5== | ||
| + | תהי f פונקציה רציפה בקטע <math>(a,b]</math> וגזירה בקטע <math>(a,b)</math> | ||
| + | ===א=== | ||
| + | נניח כי f אינה רציפה בקטע הסגור <math>[a,b]</math> לכל הצבה של <math>f(a)</math>. הוכח כי הנגזרת <math>f'</math> אינה חסומה מלעיל ואינה חסומה מלרע בקטע <math>(a,b]</math> | ||
| + | |||
| + | ===ב=== | ||
| + | הוכח שהכיוון ההפוך אינו נכון באופן כללי: תן דוגמא לפונקציה f כך שהנגזרת <math>f'</math> אינה חסומה מלעיל ואינה חסומה מלרע בקטע <math>(a,b]</math>, ואילו f רציפה בקטע הסגור <math>[a,b]</math>. | ||
גרסה מ־14:13, 5 באפריל 2012
1
קבע האם הטורים הבאים מתכנסים בהחלט/בתנאי/מתבדרים
א
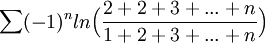
ב
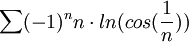
2
חשב את הגבולות הבאים
א
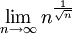
ב
![\lim_{x\rightarrow\infty}x\Big[ln^2(x+1)-ln^2(x-1)\Big]](/images/math/7/a/e/7aef37004bc79425ac7448464186a0cb.png)
3
א
הוכח כי לכל x ממשי מתקיים
ב
הוכיח כי לכל x שלילי מתקיים
4
א
יהיו f,g פונקציות רציפות בכל הממשיים המקיימות 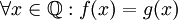
הוכח כי 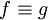 על כל הממשיים.
על כל הממשיים.
ב
מצא לאילו ערכי 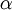 ובאילו נקודות הפונקציה הבאה גזירה:
ובאילו נקודות הפונקציה הבאה גזירה:
5
תהי f פונקציה רציפה בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וגזירה בקטע
וגזירה בקטע 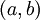
א
נניח כי f אינה רציפה בקטע הסגור ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) לכל הצבה של
לכל הצבה של 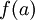 . הוכח כי הנגזרת
. הוכח כי הנגזרת 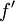 אינה חסומה מלעיל ואינה חסומה מלרע בקטע
אינה חסומה מלעיל ואינה חסומה מלרע בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png)
ב
הוכח שהכיוון ההפוך אינו נכון באופן כללי: תן דוגמא לפונקציה f כך שהנגזרת 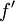 אינה חסומה מלעיל ואינה חסומה מלרע בקטע
אינה חסומה מלעיל ואינה חסומה מלרע בקטע ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) , ואילו f רציפה בקטע הסגור
, ואילו f רציפה בקטע הסגור ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.