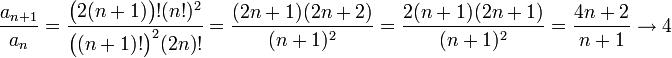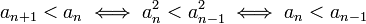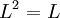הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מדמח/פתרון בוחן 1"
(←ב) |
יהודה שמחה (שיחה | תרומות) |
||
| (6 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[קטגוריה:פתרון מבחנים]][[קטגוריה:אינפי]] | ||
| + | [[מדיה:11Infi1CSBohan1.pdf|בוחן 1 לתלמידי מדעי המחשב]] | ||
| + | |||
==1== | ==1== | ||
| + | <math>L</math> הנו גבול הסדרה <math>a_n</math> אם לכל <math>\varepsilon>0</math> קיים מקום בסדרה <math>N</math> כך שלכל <math>n>N</math> מתקיים <math>|a_n-L|<\varepsilon</math> . | ||
| − | + | <math>L</math> '''אינו''' גבול הסדרה <math>a_n</math> אם '''קיים''' <math>\varepsilon>0</math> כך ש'''לכל''' מקום <math>N</math> בסדרה '''קיים''' <math>n>N</math> כך ש- <math>|a_n-L|\ge\varepsilon</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
==2== | ==2== | ||
| שורה 13: | שורה 14: | ||
==4== | ==4== | ||
| + | כיון שהאבר הראשון חיובי, ושאר האברים הם ריבועים, קל לראות כי כל הסדרה חיובית. לכן | ||
| + | :<math>a_{n+1}<a_n\iff a_n^2<a_{n-1}^2\iff a_n<a_{n-1}</math> | ||
| + | ניתן על כן להוכיח באינדוקציה כי מונוטוניות הסדרה נקבעת על-ידי הזוג הראשון. כאשר <math>c>1</math> הסדרה מונוטונית עולה, כאשר <math>c=1</math> קל לראות שהסדרה קבועה, וכאשר <math>0<c<1</math> הסדרה מונוטונית יורדת. | ||
| − | + | כאשר הסדרה מונוטונית קבועה, היא קבוע <math>1</math> ולכן זהו גבולה. | |
| − | + | כאשר הסדרה מונוטונית יורדת היא חסומה מלרע על-ידי <math>0</math> ולכן מתכנסת (מונוטונית וחסומה). נמצא את גבולה: | |
| − | + | נסמן <math>\lim\limits_{n\to\infty}a_n=L</math> ולכן <math>\lim\limits_{n\to\infty}a_{n+1}=L</math> ולכן: | |
| + | :<math>L^2=L</math> | ||
| + | כלומר <math>L=1</math> או <math>L=0</math> . כיון שאנו עוסקים במקרה בו <math>c<1</math> והסדרה מונוטונית יורדת, <math>L=\lim\limits_{n\to\infty}a_n\le c<1</math> ולכן <math>L=0</math> . | ||
| − | + | באופן דומה, כאשר הסדרה מונוטונית עולה, אם היא הייתה מתכנסת גבולה היה גדול מ-1 בסתירה. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | באופן דומה, כאשר הסדרה מונוטונית עולה, אם היא הייתה מתכנסת גבולה היה גדול | + | |
==5== | ==5== | ||
| − | |||
משיעורי הבית | משיעורי הבית | ||
| שורה 40: | שורה 34: | ||
===א=== | ===א=== | ||
| − | חסומה כפול שואפת | + | חסומה כפול שואפת ל-0 לכן שואף ל-0 |
===ב=== | ===ב=== | ||
| − | <math>\sqrt[n]{9^{n+1}-3^{2n}}=\sqrt[n]{9\ | + | <math>\sqrt[n]{9^{n+1}-3^{2n}}=\sqrt[n]{9\cdot9^n-9^{n}}=\sqrt[n]{9^n\cdot8}=9\sqrt[n]8\to9</math> |
===ג=== | ===ג=== | ||
| − | <math>L=\frac{L^2}{2}+\frac{ | + | <math>L=\frac{L^2}{2}+\frac12</math> ולכן <math>L=1</math> |
| + | |||
| + | ===ד=== | ||
| + | <math>\left(1+\frac{3n}{n^2+1}\right)^n=\left(1+\frac1{\frac{n}{3}+\frac1{3n}}\right)^{n\cdot\frac{\frac{n}{3}+\frac1{3n}}{\frac{n}{3}+\frac1{3n}}}=\left(1+\frac1{\frac{n}{3}+\frac1{3n}}\right)^{\left(\frac{n}{3}+\frac1{3n}\right)\cdot{\frac{n}{\frac{n}{3}+\frac1{3n}}}}\to e^3</math> | ||
| + | |||
| + | ===ה=== | ||
| + | לפי משפט אם הגבול <math>\lim\limits_{n\to\infty}\dfrac{a_{n+1}}{a_n}=L</math> קיים, אזי מתקיים <math>\lim\limits_{n\to\infty}\sqrt[n]{a_n}=L</math> (בכיוון ההפוך זה לא נכון) | ||
| + | |||
| + | לכן מספיק לחשב את הגבול הראשון, במקרה זה: | ||
| + | |||
| + | <math>\dfrac{a_{n+1}}{a_n}=\frac{\big(2(n+1)\big)!(n!)^2}{\big((n+1)!\big)^2(2n)!}=\frac{(2n+1)(2n+2)}{(n+1)^2}=\frac{2(n+1)(2n+1)}{(n+1)^2}=\frac{4n+2}{n+1}\to 4</math> | ||
גרסה אחרונה מ־05:24, 19 ביוני 2017
1
 הנו גבול הסדרה
הנו גבול הסדרה  אם לכל
אם לכל  קיים מקום בסדרה
קיים מקום בסדרה 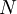 כך שלכל
כך שלכל 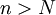 מתקיים
מתקיים 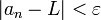 .
.
 אינו גבול הסדרה
אינו גבול הסדרה  אם קיים
אם קיים  כך שלכל מקום
כך שלכל מקום 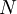 בסדרה קיים
בסדרה קיים 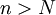 כך ש-
כך ש- 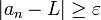 .
.
2
משיעורי הבית
3
משיעורי הבית
4
כיון שהאבר הראשון חיובי, ושאר האברים הם ריבועים, קל לראות כי כל הסדרה חיובית. לכן
ניתן על כן להוכיח באינדוקציה כי מונוטוניות הסדרה נקבעת על-ידי הזוג הראשון. כאשר 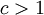 הסדרה מונוטונית עולה, כאשר
הסדרה מונוטונית עולה, כאשר 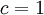 קל לראות שהסדרה קבועה, וכאשר
קל לראות שהסדרה קבועה, וכאשר 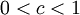 הסדרה מונוטונית יורדת.
הסדרה מונוטונית יורדת.
כאשר הסדרה מונוטונית קבועה, היא קבוע 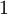 ולכן זהו גבולה.
ולכן זהו גבולה.
כאשר הסדרה מונוטונית יורדת היא חסומה מלרע על-ידי  ולכן מתכנסת (מונוטונית וחסומה). נמצא את גבולה:
ולכן מתכנסת (מונוטונית וחסומה). נמצא את גבולה:
נסמן 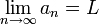 ולכן
ולכן 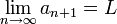 ולכן:
ולכן:
כלומר 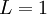 או
או 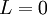 . כיון שאנו עוסקים במקרה בו
. כיון שאנו עוסקים במקרה בו 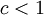 והסדרה מונוטונית יורדת,
והסדרה מונוטונית יורדת, 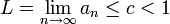 ולכן
ולכן 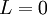 .
.
באופן דומה, כאשר הסדרה מונוטונית עולה, אם היא הייתה מתכנסת גבולה היה גדול מ-1 בסתירה.
5
משיעורי הבית
6
א
חסומה כפול שואפת ל-0 לכן שואף ל-0
ב
![\sqrt[n]{9^{n+1}-3^{2n}}=\sqrt[n]{9\cdot9^n-9^{n}}=\sqrt[n]{9^n\cdot8}=9\sqrt[n]8\to9](/images/math/a/3/6/a366c184b1b1b017cc9294181e71483f.png)
ג
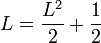 ולכן
ולכן 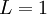
ד
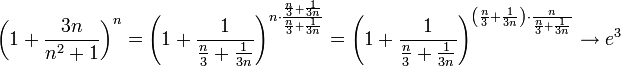
ה
לפי משפט אם הגבול 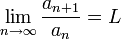 קיים, אזי מתקיים
קיים, אזי מתקיים ![\lim\limits_{n\to\infty}\sqrt[n]{a_n}=L](/images/math/0/8/1/0811d7fcd52ba7197c6bc9fee0b1c1b0.png) (בכיוון ההפוך זה לא נכון)
(בכיוון ההפוך זה לא נכון)
לכן מספיק לחשב את הגבול הראשון, במקרה זה: