הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מדמח/פתרון בוחן 2"
יהודה שמחה (שיחה | תרומות) מ |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 3: | שורה 3: | ||
==1== | ==1== | ||
| − | תנאי הכרחי להתכנסות הטור <math>\ | + | תנאי הכרחי להתכנסות הטור <math>\displaystyle\sum_{n=1}^\infty a_n</math> הוא התכנסות הסדרה <math>a_n\to0</math> . תנאי זה הכרחי אבל אינו מספיק. |
טור מתכנס בתנאי הנו טור המתכנס, אבל אינו מתכנס בהחלט. | טור מתכנס בתנאי הנו טור המתכנס, אבל אינו מתכנס בהחלט. | ||
| שורה 12: | שורה 12: | ||
===ב=== | ===ב=== | ||
| − | כיון שהטור <math>\ | + | כיון שהטור <math>\displaystyle\sum_{n=1}^\infty a_n</math> מתכנס, אזי הסדרה שלו שואפת ל-0. לכן |
| − | <math>\ | + | <math>\dfrac{|a_n\cdot b_n|}{|b_n|}=|a_n|\to0</math> |
| − | ולכן לפי מבחן ההשוואה השני לטורים חיוביים, הטור <math>\ | + | ולכן לפי מבחן ההשוואה השני לטורים חיוביים, הטור <math>\displaystyle\sum_{n=1}^\infty|a_n\cdot b_n|</math> מתכנס, כלומר הטור <math>\displaystyle\sum_{n=1}^\infty a_n\cdot b_n</math> מתכנס בהחלט. |
===ג=== | ===ג=== | ||
הוכחה: | הוכחה: | ||
| − | כיון שהטור <math>\ | + | כיון שהטור <math>\displaystyle\sum_{n=1}^\infty a_n</math> מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה <math>\dfrac1{a_n}</math> לא חסומה או לא-מוגדרת ובכל מקרה אינה שואפת ל-0 ולכן הטור <math>\displaystyle\sum_{n=1}^\infty\dfrac1{a_n}</math> מתבדר. |
===ד=== | ===ד=== | ||
הפרכה: | הפרכה: | ||
| − | <math>a_n=\ | + | <math>a_n=\dfrac{(-1)^n}{\sqrt{n}}</math> מתכנס לפי לייבניץ, אבל <math>a_n^2=\dfrac1n</math> מתבדר. |
==3== | ==3== | ||
| שורה 33: | שורה 33: | ||
===ב=== | ===ב=== | ||
| − | <math>2^n+(-1)^n2^n\ | + | <math>2^n+(-1)^n2^n\le2\cdot2^n</math> |
ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס | ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס | ||
| − | <math>2\ | + | <math>2\displaystyle\sum_{n=1}^\infty\left(\dfrac23\right)^n</math> |
ולכן מתכנס. | ולכן מתכנס. | ||
| שורה 50: | שורה 50: | ||
נפעיל את מבחן המנה: | נפעיל את מבחן המנה: | ||
| − | <math>\ | + | <math>\dfrac{a_{n+1}}{a_n}=\dfrac{\sqrt{2-\sqrt{2+\sqrt{2+\cdots}}}}{\sqrt{2-\sqrt{2+\cdots}}}</math> |
נכפיל בצמוד של המונה למעלה ולמטה לקבל: | נכפיל בצמוד של המונה למעלה ולמטה לקבל: | ||
| − | <math>\frac{\sqrt{2-\sqrt{2+\sqrt{2+\cdots}}}}{\sqrt{2-\sqrt{2+\cdots}}}=\frac{4-2-\sqrt{2+\cdots}}{\sqrt{2\sqrt{2+\cdots}} | + | <math> |
| − | + | \begin{align} | |
| − | + | \frac{\sqrt{2-\sqrt{2+\sqrt{2+\cdots}}}}{\sqrt{2-\sqrt{2+\cdots}}}=\frac{4-2-\sqrt{2+\cdots}}{\sqrt{2\sqrt{2+\cdots}}\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}}=\frac{2-\sqrt{2+\cdots}}{\sqrt{2-\sqrt{2+\cdots}}\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}}=\\\\ | |
| − | + | \frac{\sqrt{2-\sqrt{2+\cdots}}}{\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}}\le \frac{\sqrt{2-\sqrt{2+\cdots}}}{\sqrt2}<1 | |
| − | + | \end{align} | |
| − | + | </math> | |
| − | + | ||
ולכן הטור מתכנס. | ולכן הטור מתכנס. | ||
| שורה 66: | שורה 65: | ||
==4== | ==4== | ||
===א=== | ===א=== | ||
| − | מתכונות פונקציות הקוסינוס ניתן לראות שאנו מקבלים סכום של טורים בעלי סדרה השואפת מונוטונית | + | מתכונות פונקציות הקוסינוס ניתן לראות שאנו מקבלים סכום של טורים בעלי סדרה השואפת מונוטונית ל-0 עם סימנים מתחלפים ולכן מתכנס לפי לייבניץ. |
ידוע שהטור אינו מתכנס בהחלט, ולכן סה"כ הטור '''מתכנס בתנאי'''. | ידוע שהטור אינו מתכנס בהחלט, ולכן סה"כ הטור '''מתכנס בתנאי'''. | ||
===ב=== | ===ב=== | ||
| − | הטור מתבדר שכן סכום | + | הטור מתבדר שכן סכום אבריו השליליים מתכנס בעוד סכום אבריו החיוביים מתבדר. |
===ג=== | ===ג=== | ||
| − | הטור מתכנס בהחלט לפי מבחן ההשוואה הראשון עם הטור <math>\ | + | הטור מתכנס בהחלט לפי מבחן ההשוואה הראשון עם הטור <math>\displaystyle\sum_{n=1}^\infty\dfrac1{n^2}</math> . |
גרסה אחרונה מ־05:32, 19 ביוני 2017
תוכן עניינים
1
תנאי הכרחי להתכנסות הטור 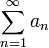 הוא התכנסות הסדרה
הוא התכנסות הסדרה 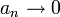 . תנאי זה הכרחי אבל אינו מספיק.
. תנאי זה הכרחי אבל אינו מספיק.
טור מתכנס בתנאי הנו טור המתכנס, אבל אינו מתכנס בהחלט.
2
א
ברור כי 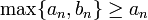 ולכן לפי מבחן ההשוואה הראשון לטורים חיוביים הטור מתבדר.
ולכן לפי מבחן ההשוואה הראשון לטורים חיוביים הטור מתבדר.
ב
כיון שהטור 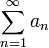 מתכנס, אזי הסדרה שלו שואפת ל-0. לכן
מתכנס, אזי הסדרה שלו שואפת ל-0. לכן
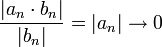
ולכן לפי מבחן ההשוואה השני לטורים חיוביים, הטור 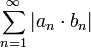 מתכנס, כלומר הטור
מתכנס, כלומר הטור 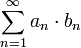 מתכנס בהחלט.
מתכנס בהחלט.
ג
הוכחה:
כיון שהטור 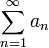 מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה
מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה 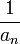 לא חסומה או לא-מוגדרת ובכל מקרה אינה שואפת ל-0 ולכן הטור
לא חסומה או לא-מוגדרת ובכל מקרה אינה שואפת ל-0 ולכן הטור 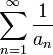 מתבדר.
מתבדר.
ד
הפרכה:
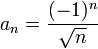 מתכנס לפי לייבניץ, אבל
מתכנס לפי לייבניץ, אבל 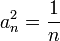 מתבדר.
מתבדר.
3
א
ב
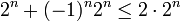
ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס
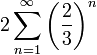
ולכן מתכנס.
ג
ד
ה
נפעיל את מבחן המנה:
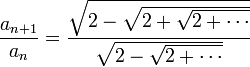
נכפיל בצמוד של המונה למעלה ולמטה לקבל:
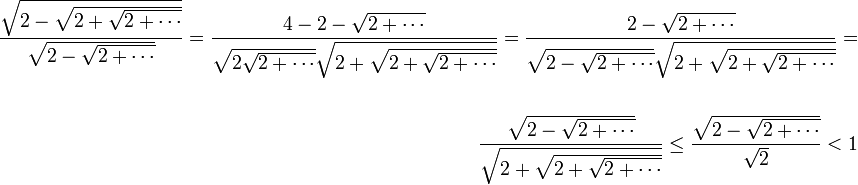
ולכן הטור מתכנס.
4
א
מתכונות פונקציות הקוסינוס ניתן לראות שאנו מקבלים סכום של טורים בעלי סדרה השואפת מונוטונית ל-0 עם סימנים מתחלפים ולכן מתכנס לפי לייבניץ.
ידוע שהטור אינו מתכנס בהחלט, ולכן סה"כ הטור מתכנס בתנאי.
ב
הטור מתבדר שכן סכום אבריו השליליים מתכנס בעוד סכום אבריו החיוביים מתבדר.
ג
הטור מתכנס בהחלט לפי מבחן ההשוואה הראשון עם הטור 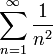 .
.