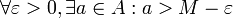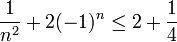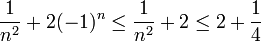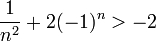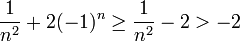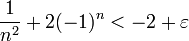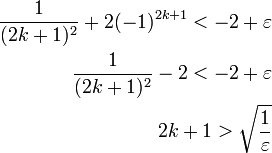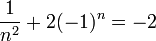הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/חסמים"
(יצירת דף עם התוכן "'''הגדרה:''' תהי U סדורה ותהי תת קבוצה <math>A\subseteq U</math>, אזי: *<math>M\in U</math> נקרא '''חסם מלעיל''' של A אם ...") |
(←חסמים) |
||
| (14 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | '''הגדרה:''' תהי U סדורה ותהי תת קבוצה <math>A\subseteq U</math>, אזי: | + | [[חשבון אינפיניטיסימלי 1 - מערך תרגול|חזרה לרשימת הנושאים]] |
| − | *<math>M\in U</math> נקרא '''חסם מלעיל''' של A אם <math>\forall a\in A:a\ | + | =חסמים= |
| − | *<math>m\in U</math> נקרא '''חסם מלרע''' של A אם <math>\forall a\in A:a\ | + | '''הגדרה:''' תהי <math>U</math> סדורה ותהי תת-קבוצה <math>A\subseteq U</math> , אזי: |
| − | *חסם מלעיל של A נקרא '''מקסימום''' אם הוא שייך לקבוצה A | + | *<math>M\in U</math> נקרא '''חסם מלעיל''' של <math>A</math> אם <math>\forall a\in A:a\le M</math> |
| − | *חסם מלרע של A נקרא '''מינימום''' אם הוא שייך לקבוצה A | + | *<math>m\in U</math> נקרא '''חסם מלרע''' של <math>A</math> אם <math>\forall a\in A:a\ge m</math> |
| − | *חסם מלעיל של A נקרא '''החסם העליון''' של A אם אין ל-A חסם מלעיל קטן ממש ממנו. (כלומר, החסם העליון הוא המינימום מבין קבוצת חסמי המלעיל, אם כזה קיים.) | + | *חסם מלעיל של <math>A</math> נקרא '''מקסימום''' אם הוא שייך לקבוצה <math>A</math> |
| − | *חסם מלרע של A נקרא '''החסם התחתון''' של A אם אין ל-A חסם מלרע גדול ממש ממנו. (כלומר, החסם התחתון הוא המקסימום מבין קבוצת חסמי המלרע, אם כזה קיים.) | + | *חסם מלרע של <math>A</math> נקרא '''מינימום''' אם הוא שייך לקבוצה <math>A</math> |
| + | *חסם מלעיל של <math>A</math> נקרא '''החסם העליון''' של <math>A</math> אם אין ל- <math>A</math> חסם מלעיל קטן ממש ממנו. (כלומר, החסם העליון הוא המינימום מבין קבוצת חסמי המלעיל, אם כזה קיים.) | ||
| + | *חסם מלרע של <math>A</math> נקרא '''החסם התחתון''' של <math>A</math> אם אין ל- <math>A</math> חסם מלרע גדול ממש ממנו. (כלומר, החסם התחתון הוא המקסימום מבין קבוצת חסמי המלרע, אם כזה קיים.) | ||
| − | '''אקסיומת השלימות של המספרים הממשיים''' - לכל <math>A\subseteq\ | + | שימו לב לשלילות הבאות: |
| + | *<math>M</math> אינו חסם מלעיל אם"ם קיים אבר <math>a>M</math> | ||
| + | *<math>m</math> אינו חסם מלרע אם"ם קיים אבר <math>a<m</math> | ||
| + | *<math>M</math> אינו חסם עליון אם"ם הוא אינו חסם מלעיל או שקיים חסם מלעיל הקטן ממש ממנו. | ||
| + | *<math>m</math> אינו חסם תחתון אם"ם הוא אינו חסם מלרע או שקיים חסם מלרע הגדול ממש ממנו. | ||
| + | |||
| + | |||
| + | '''אקסיומת השלימות של המספרים הממשיים''' - לכל <math>A\subseteq\R</math> חסומה מלעיל (מלרע) קיים חסם עליון (תחתון). | ||
| + | |||
| + | ניתן לראות ששדה הרציונאליים אינו שלם. נגדיר קבוצה של כל המספרים הרציונאליים אשר בריבוע קטנים משתים (כלומר המספרים שקטנים מ- <math>\sqrt2</math>). לכל חסם מלעיל של הקבוצה, יש חסם מלעיל הקרוב יותר ל- <math>\sqrt2</math> הקטן ממנו (שכן <math>\sqrt2</math> עצמו אינו רציונאלי ולכן לא יכול להוות חסם מלעיל). לכן אין אף חסם עליון לקבוצה החסומה מלעיל שבנינו. | ||
| + | |||
| + | |||
| + | ;משפט. | ||
| + | תהי <math>A\subseteq\R</math> חסומה מלעיל אזי: | ||
| + | *<math>M</math> חסם עליון של <math>A</math> '''אם"ם''' <math>M</math> חסם מלעיל של <math>A</math> וגם לכל <math>\varepsilon>0</math> קיים <math>a\in A</math> כך ש- <math>a>M-\varepsilon</math> | ||
| + | *<math>m</math> חסם תחתון של <math>A</math> '''אם"ם''' <math>m</math> חסם מלרע של <math>A</math> וגם לכל <math>\varepsilon>0</math> קיים <math>a\in A</math> כך ש- <math>a<m+\varepsilon</math> | ||
| + | |||
| + | |||
| + | '''במילים:''' <math>M</math> חסם עליון אם הוא חסם מלעיל וגם אין חסם מלעיל הקטן ממנו. כלומר, כל מספר הקטן ממנו אינו חסם מלעיל. כלומר, אם נקטין את <math>M</math> בגודל כלשהו שאינו 0 נקבל מספר שאינו חסם מלעיל. מספר אינו חסם מלעיל אם"ם יש אבר בקבוצה הגדול ממנו. (ניסוח דומה עבור החסם התחתון.) | ||
| + | |||
| + | ;הוכחה. | ||
| + | נניח <math>M</math> חסם עליון. מתוך ההגדרה של חסם עליון נובע בפרט ש- <math>M</math> חסם מלעיל. נותר להוכיח כי | ||
| + | :<math>\forall\varepsilon>0,\exists a\in A:a>M-\varepsilon</math> | ||
| + | נניח בשלילה כי קיים <math>\varepsilon>0</math> כל שלכל האברים <math>a\in A</math> מתקיים <math>a\le M-\varepsilon</math> . | ||
| + | |||
| + | לכן, לפי ההגדרה <math>M-\varepsilon</math> הוא חסם מלעיל של הקבוצה. מכיון שאפסילון גדול מ-0, <math>M-\varepsilon</math> הוא חסם מלעיל קטן ממש מהחסם העליון <math>M</math> , בסתירה לכך שהוא חסם המלעיל הקטן ביותר. | ||
| + | |||
| + | |||
| + | ;תרגיל. | ||
| + | תהי <math>A=\left\{\dfrac1{n^2}+2(-1)^n\Big|n\in\N\right\}</math> מצא חסם עליון, חסם עליון, מינימום ומקסימום (אם הם קיימים). | ||
| + | |||
| + | ראשית, נביט במספר אברים מהקבוצה על מנת לקבל הערכה כלשהי: <math>A=\left\{-1,2\dfrac14,-1\dfrac89,2\dfrac1{16},\ldots\right\}</math> | ||
| + | |||
| + | אנחנו מעריכים כי שתים ורבע הוא מקסימום (ולכן גם חסם עליון, הרי מקסימום הנו תמיד חסם עליון אם הוא קיים), ואנו מעריכים כי 2- הנו חסם תחתון שאינו בקבוצה ולכן אין מינימום. נוכיח את כל זה. | ||
| + | |||
| + | *נוכיח כי שתים ורבע חסם מלעיל (ואז מכיוון שהוא בקבוצה הוא מקסימום ולכן חסם עליון). צ"ל שכל אבר בקבוצה קטן או שווה לו, ולכן צ"ל שלכל <math>n</math> טבעי מתקיים | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n\le2+\dfrac14</math> | ||
| + | |||
| + | עבור <math>n=1</math> זה ברור. אם <math>n\ge2</math> ניתן לומר | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n\le\dfrac1{n^2}+2\le2+\dfrac14</math> | ||
| + | *כעת נוכיח כי מינוס שתים הינו חסם מלרע, כלומר לכל n טבעי מתקיים: | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n>-2</math> | ||
| + | אבל | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n\ge\dfrac1{n^2}-2>-2</math> | ||
| + | |||
| + | *כעת נוכיח כי בנוסף, לכל <math>\varepsilon>0</math> קיים אבר <math>a</math> בקבוצה כך ש- <math>a<-2+\varepsilon</math> . | ||
| + | |||
| + | יהי <math>\varepsilon>0</math> , צ"ל <math>n</math> טבעי כך ש: | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n<-2+\varepsilon</math> | ||
| + | |||
| + | מכיון שצריך להראות ש'''קיים''' <math>n</math> טבעי אחד כזה, מספיק בפרט למצוא אחד כזה אי-זוגי. לכן ננסה למצוא | ||
| + | :<math>\begin{align}\dfrac1{(2k+1)^2}+2(-1)^{2k+1}<-2+\varepsilon\\\dfrac1{(2k+1)^2}-2<-2+\varepsilon\\2k+1>\sqrt{\dfrac1{\varepsilon}}\end{align}</math> | ||
| + | |||
| + | תמיד ניתן למצוא <math>k</math> טבעי כזה אחרת קבוצת הטבעיים הייתה חסומה, משל. | ||
| + | |||
| + | |||
| + | לכן הוכחנו כי <math>-2</math> הנו חסם תחתון. נותר להוכיח כי לא קיים מינימום | ||
| + | |||
| + | *נוכיח כי החסם התחתון <math>-2</math> אינו שייך לקבוצה ולכן לא קיים מינימום (אחרת הוא היה חסם תחתון). כלומר, נוכיח כי לא קיים <math>n</math> טבעי כך ש: | ||
| + | :<math>\dfrac1{n^2}+2(-1)^n=-2</math> | ||
| + | |||
| + | אבל כבר הראינו שאברי הקבוצה גדולים ממש ולא שווים ל-2-. | ||
גרסה אחרונה מ־12:10, 22 במאי 2021
חסמים
הגדרה: תהי 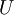 סדורה ותהי תת-קבוצה
סדורה ותהי תת-קבוצה 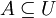 , אזי:
, אזי:
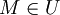 נקרא חסם מלעיל של
נקרא חסם מלעיל של  אם
אם 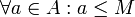
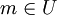 נקרא חסם מלרע של
נקרא חסם מלרע של  אם
אם 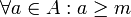
- חסם מלעיל של
 נקרא מקסימום אם הוא שייך לקבוצה
נקרא מקסימום אם הוא שייך לקבוצה 
- חסם מלרע של
 נקרא מינימום אם הוא שייך לקבוצה
נקרא מינימום אם הוא שייך לקבוצה 
- חסם מלעיל של
 נקרא החסם העליון של
נקרא החסם העליון של  אם אין ל-
אם אין ל-  חסם מלעיל קטן ממש ממנו. (כלומר, החסם העליון הוא המינימום מבין קבוצת חסמי המלעיל, אם כזה קיים.)
חסם מלעיל קטן ממש ממנו. (כלומר, החסם העליון הוא המינימום מבין קבוצת חסמי המלעיל, אם כזה קיים.) - חסם מלרע של
 נקרא החסם התחתון של
נקרא החסם התחתון של  אם אין ל-
אם אין ל-  חסם מלרע גדול ממש ממנו. (כלומר, החסם התחתון הוא המקסימום מבין קבוצת חסמי המלרע, אם כזה קיים.)
חסם מלרע גדול ממש ממנו. (כלומר, החסם התחתון הוא המקסימום מבין קבוצת חסמי המלרע, אם כזה קיים.)
שימו לב לשלילות הבאות:
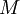 אינו חסם מלעיל אם"ם קיים אבר
אינו חסם מלעיל אם"ם קיים אבר 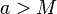
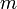 אינו חסם מלרע אם"ם קיים אבר
אינו חסם מלרע אם"ם קיים אבר 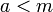
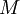 אינו חסם עליון אם"ם הוא אינו חסם מלעיל או שקיים חסם מלעיל הקטן ממש ממנו.
אינו חסם עליון אם"ם הוא אינו חסם מלעיל או שקיים חסם מלעיל הקטן ממש ממנו.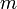 אינו חסם תחתון אם"ם הוא אינו חסם מלרע או שקיים חסם מלרע הגדול ממש ממנו.
אינו חסם תחתון אם"ם הוא אינו חסם מלרע או שקיים חסם מלרע הגדול ממש ממנו.
אקסיומת השלימות של המספרים הממשיים - לכל 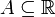 חסומה מלעיל (מלרע) קיים חסם עליון (תחתון).
חסומה מלעיל (מלרע) קיים חסם עליון (תחתון).
ניתן לראות ששדה הרציונאליים אינו שלם. נגדיר קבוצה של כל המספרים הרציונאליים אשר בריבוע קטנים משתים (כלומר המספרים שקטנים מ- 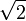 ). לכל חסם מלעיל של הקבוצה, יש חסם מלעיל הקרוב יותר ל-
). לכל חסם מלעיל של הקבוצה, יש חסם מלעיל הקרוב יותר ל- 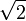 הקטן ממנו (שכן
הקטן ממנו (שכן 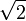 עצמו אינו רציונאלי ולכן לא יכול להוות חסם מלעיל). לכן אין אף חסם עליון לקבוצה החסומה מלעיל שבנינו.
עצמו אינו רציונאלי ולכן לא יכול להוות חסם מלעיל). לכן אין אף חסם עליון לקבוצה החסומה מלעיל שבנינו.
- משפט.
תהי 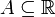 חסומה מלעיל אזי:
חסומה מלעיל אזי:
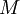 חסם עליון של
חסם עליון של  אם"ם
אם"ם 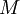 חסם מלעיל של
חסם מלעיל של  וגם לכל
וגם לכל  קיים
קיים 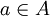 כך ש-
כך ש- 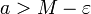
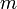 חסם תחתון של
חסם תחתון של  אם"ם
אם"ם 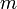 חסם מלרע של
חסם מלרע של  וגם לכל
וגם לכל  קיים
קיים 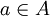 כך ש-
כך ש- 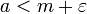
במילים: 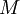 חסם עליון אם הוא חסם מלעיל וגם אין חסם מלעיל הקטן ממנו. כלומר, כל מספר הקטן ממנו אינו חסם מלעיל. כלומר, אם נקטין את
חסם עליון אם הוא חסם מלעיל וגם אין חסם מלעיל הקטן ממנו. כלומר, כל מספר הקטן ממנו אינו חסם מלעיל. כלומר, אם נקטין את 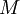 בגודל כלשהו שאינו 0 נקבל מספר שאינו חסם מלעיל. מספר אינו חסם מלעיל אם"ם יש אבר בקבוצה הגדול ממנו. (ניסוח דומה עבור החסם התחתון.)
בגודל כלשהו שאינו 0 נקבל מספר שאינו חסם מלעיל. מספר אינו חסם מלעיל אם"ם יש אבר בקבוצה הגדול ממנו. (ניסוח דומה עבור החסם התחתון.)
- הוכחה.
נניח 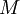 חסם עליון. מתוך ההגדרה של חסם עליון נובע בפרט ש-
חסם עליון. מתוך ההגדרה של חסם עליון נובע בפרט ש- 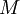 חסם מלעיל. נותר להוכיח כי
חסם מלעיל. נותר להוכיח כי
נניח בשלילה כי קיים  כל שלכל האברים
כל שלכל האברים 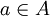 מתקיים
מתקיים 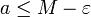 .
.
לכן, לפי ההגדרה 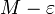 הוא חסם מלעיל של הקבוצה. מכיון שאפסילון גדול מ-0,
הוא חסם מלעיל של הקבוצה. מכיון שאפסילון גדול מ-0, 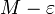 הוא חסם מלעיל קטן ממש מהחסם העליון
הוא חסם מלעיל קטן ממש מהחסם העליון 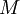 , בסתירה לכך שהוא חסם המלעיל הקטן ביותר.
, בסתירה לכך שהוא חסם המלעיל הקטן ביותר.
- תרגיל.
תהי 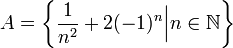 מצא חסם עליון, חסם עליון, מינימום ומקסימום (אם הם קיימים).
מצא חסם עליון, חסם עליון, מינימום ומקסימום (אם הם קיימים).
ראשית, נביט במספר אברים מהקבוצה על מנת לקבל הערכה כלשהי: 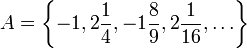
אנחנו מעריכים כי שתים ורבע הוא מקסימום (ולכן גם חסם עליון, הרי מקסימום הנו תמיד חסם עליון אם הוא קיים), ואנו מעריכים כי 2- הנו חסם תחתון שאינו בקבוצה ולכן אין מינימום. נוכיח את כל זה.
- נוכיח כי שתים ורבע חסם מלעיל (ואז מכיוון שהוא בקבוצה הוא מקסימום ולכן חסם עליון). צ"ל שכל אבר בקבוצה קטן או שווה לו, ולכן צ"ל שלכל
 טבעי מתקיים
טבעי מתקיים
עבור 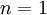 זה ברור. אם
זה ברור. אם 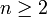 ניתן לומר
ניתן לומר
- כעת נוכיח כי מינוס שתים הינו חסם מלרע, כלומר לכל n טבעי מתקיים:
אבל
- כעת נוכיח כי בנוסף, לכל
 קיים אבר
קיים אבר  בקבוצה כך ש-
בקבוצה כך ש- 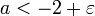 .
.
יהי  , צ"ל
, צ"ל  טבעי כך ש:
טבעי כך ש:
מכיון שצריך להראות שקיים  טבעי אחד כזה, מספיק בפרט למצוא אחד כזה אי-זוגי. לכן ננסה למצוא
טבעי אחד כזה, מספיק בפרט למצוא אחד כזה אי-זוגי. לכן ננסה למצוא
תמיד ניתן למצוא  טבעי כזה אחרת קבוצת הטבעיים הייתה חסומה, משל.
טבעי כזה אחרת קבוצת הטבעיים הייתה חסומה, משל.
לכן הוכחנו כי 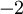 הנו חסם תחתון. נותר להוכיח כי לא קיים מינימום
הנו חסם תחתון. נותר להוכיח כי לא קיים מינימום
- נוכיח כי החסם התחתון
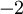 אינו שייך לקבוצה ולכן לא קיים מינימום (אחרת הוא היה חסם תחתון). כלומר, נוכיח כי לא קיים
אינו שייך לקבוצה ולכן לא קיים מינימום (אחרת הוא היה חסם תחתון). כלומר, נוכיח כי לא קיים  טבעי כך ש:
טבעי כך ש:
אבל כבר הראינו שאברי הקבוצה גדולים ממש ולא שווים ל-2-.