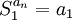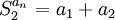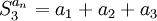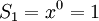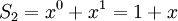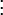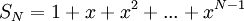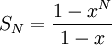הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/הגדרה"
(←הגדרות בסיסיות של טורים) |
(←הגדרות בסיסיות של טורים) |
||
| שורה 90: | שורה 90: | ||
ניזכר בתרגילים מ[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/קושי|סדרות קושי]]. נשים לב כי סדרת הסכומים החלקיים של הטור <math>\sum\frac{1}{n}</math> (הנקרא לעיתים הטור '''ההרמוני''') מוגדרת על ידי כלל הנסיגה <math>S_{N+1}=S_N+\frac{1}{n+1}</math>. כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר. | ניזכר בתרגילים מ[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/קושי|סדרות קושי]]. נשים לב כי סדרת הסכומים החלקיים של הטור <math>\sum\frac{1}{n}</math> (הנקרא לעיתים הטור '''ההרמוני''') מוגדרת על ידי כלל הנסיגה <math>S_{N+1}=S_N+\frac{1}{n+1}</math>. כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר. | ||
| − | באופן דומה, | + | באופן דומה, נסיק כי הטור <math>\sum\frac{1}{n^2}</math> מתכנס. |
באופן כללי, הטור <math>\sum\frac{1}{n^\alpha}</math> מתכנס אם"ם <math>\alpha > 1</math> אבל את זה נלמד בהמשך. | באופן כללי, הטור <math>\sum\frac{1}{n^\alpha}</math> מתכנס אם"ם <math>\alpha > 1</math> אבל את זה נלמד בהמשך. | ||
| + | |||
| + | ==טורים טלסקופיים== | ||
גרסה מ־15:57, 27 בנובמבר 2011
הגדרות בסיסיות של טורים
באופן בלתי פורמלי, טור הינו סכום אינסופי של מספרים. נשאלת השאלה, האם סכום אינסופי של מספרים חיוביים עשוי להיות קטן ממספר סופי?
נענת התשובה - כן. לדוגמא, ניקח עוגה (או פאי). נחלק חצי מהעוגה לתלמיד המצטיין, חצי ממה שנשאר (רבע) ניתן לתלמיד הבא אחריו. חצי ממה שנשאר (שמינית) ניתן לתלמיד הבא אחריו. אחד חלקי שש עשרה יקבל התלמיד הבא וכן הלאה.
כמובן שלא נוכל לחלק יותר מאשר עוגה אחת ממנה התחלנו. לכן, אינטואיטיבית, 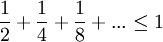
הגדרה.
נגדיר את סדרת הסכומים החלקיים 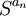 של סדרה
של סדרה  כלשהי להיות
כלשהי להיות 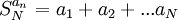 .
.
כלומר,
וכן הלאה.
הגדרה.
- אומרים כי טור הסדרה
 מתכנס אם סדרת הסכומים החלקיים
מתכנס אם סדרת הסכומים החלקיים 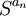 מתכנסת. (במובן הגדרת הגבול של סדרות, כמובן)
מתכנסת. (במובן הגדרת הגבול של סדרות, כמובן)
- במקרה זה אומרים כי סכום הטור שווה לגבול סדרת הסכומים החלקיים
- אומרים כי טור הסדרה
 מתכנס בהחלט אם טור הסדרה
מתכנס בהחלט אם טור הסדרה 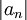 מתכנס.
מתכנס.
- אומרים כי טור מתכנס בתנאי אם הוא מתכנס, אך אינו מתכנס בהחלט.
מסמנים את טור הסדרה ב 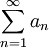
דוגמא חשובה.
נחשב את סכום הטור 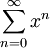
כעת, לפי הנוסחא לסכום סדרה הנדסית, מקבלים
אם כך, 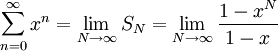
זה תרגיל בסדרות, וקל לראות כי:
- אם
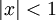 הסדרה מתכנסת ומקבלים
הסדרה מתכנסת ומקבלים 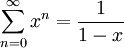
- אם
- אם
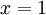 הסדרה לא מוגדרת, כיוון שאסור היה להשתמש בנוסחאת הסכום במקרה זה. קל לראות, אמנם, כי סדרת הסכומים החלקיים האמיתית שואפת לאינסוף ולכן הטור מתבדר
הסדרה לא מוגדרת, כיוון שאסור היה להשתמש בנוסחאת הסכום במקרה זה. קל לראות, אמנם, כי סדרת הסכומים החלקיים האמיתית שואפת לאינסוף ולכן הטור מתבדר
- אם
- אם
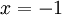 הסדרה מתבדרת וכך גם הטור
הסדרה מתבדרת וכך גם הטור
- אם
- אם
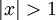 הסדרת אינה חסומה, ולכן מתבדרת ולכן הטור מתבדר.
הסדרת אינה חסומה, ולכן מתבדרת ולכן הטור מתבדר.
- אם
שימו לב: אם נתחיל את הספירה ממקום אחר, נקבל סכום אחר. 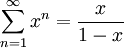 . אם כך, מספר סופי של איברים לא משפיע על התכנסות הטור, אך עשוי להשפיע על סכומו.
. אם כך, מספר סופי של איברים לא משפיע על התכנסות הטור, אך עשוי להשפיע על סכומו.
באופן כללי, סדרת הסכומים החלקיים של טור מוגדרת על ידי כלל הנסיגה 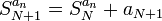 .
.
דוגמא חשובה.
ניזכר בתרגילים מסדרות קושי. נשים לב כי סדרת הסכומים החלקיים של הטור 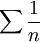 (הנקרא לעיתים הטור ההרמוני) מוגדרת על ידי כלל הנסיגה
(הנקרא לעיתים הטור ההרמוני) מוגדרת על ידי כלל הנסיגה 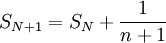 . כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר.
. כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר.
באופן דומה, נסיק כי הטור 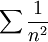 מתכנס.
מתכנס.
באופן כללי, הטור 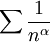 מתכנס אם"ם
מתכנס אם"ם 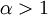 אבל את זה נלמד בהמשך.
אבל את זה נלמד בהמשך.