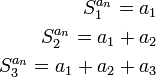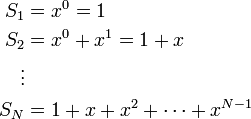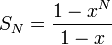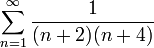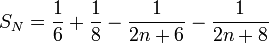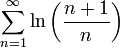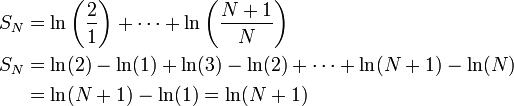הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/הגדרה"
(←טורים טלסקופיים) |
יהודה שמחה (שיחה | תרומות) |
||
| (4 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
=הגדרות בסיסיות של טורים= | =הגדרות בסיסיות של טורים= | ||
| − | + | באופן בלתי פורמלי, טור הנו '''סכום אינסופי''' של מספרים. נשאלת השאלה, האם סכום אינסופי של מספרים חיוביים עשוי להיות קטן ממספר סופי? | |
| − | באופן בלתי פורמלי, טור | + | |
נענת התשובה - כן. לדוגמא, ניקח עוגה (או פאי). נחלק חצי מהעוגה לתלמיד המצטיין, חצי ממה שנשאר (רבע) ניתן לתלמיד הבא אחריו. חצי ממה שנשאר (שמינית) ניתן לתלמיד הבא אחריו. אחד חלקי שש עשרה יקבל התלמיד הבא וכן הלאה. | נענת התשובה - כן. לדוגמא, ניקח עוגה (או פאי). נחלק חצי מהעוגה לתלמיד המצטיין, חצי ממה שנשאר (רבע) ניתן לתלמיד הבא אחריו. חצי ממה שנשאר (שמינית) ניתן לתלמיד הבא אחריו. אחד חלקי שש עשרה יקבל התלמיד הבא וכן הלאה. | ||
| − | כמובן שלא נוכל לחלק יותר מאשר '''עוגה אחת''' ממנה התחלנו. לכן, אינטואיטיבית, <math>\ | + | כמובן שלא נוכל לחלק יותר מאשר '''עוגה אחת''' ממנה התחלנו. לכן, אינטואיטיבית, <math>\dfrac12+\dfrac14+\dfrac18+\cdots\le1</math> |
| − | <font size=4 color=#3c498e> | + | <font size=4 color=#3c498e>'''הגדרה.'''</font> |
| − | '''הגדרה.''' | + | |
| − | </font> | + | |
| − | נגדיר את '''סדרת הסכומים החלקיים''' <math>S^{a_n}</math> של סדרה <math>a_n</math> כלשהי להיות <math>S^{a_n}_N = a_1+ | + | נגדיר את '''סדרת הסכומים החלקיים''' <math>S^{a_n}</math> של סדרה <math>a_n</math> כלשהי להיות <math>S^{a_n}_N=a_1+\cdots+a_N</math> . |
כלומר, | כלומר, | ||
| − | + | :<math>\begin{align}S^{a_n}_1=a_1\\S^{a_n}_2=a_1+a_2\\S^{a_n}_3=a_1+a_2+a_3\end{align}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
וכן הלאה. | וכן הלאה. | ||
| − | <font size=4 color=#3c498e> | + | <font size=4 color=#3c498e>'''הגדרה.'''</font> |
| − | '''הגדרה.''' | + | |
| − | </font> | + | |
| − | *אומרים כי טור הסדרה <math>a_n</math> '''מתכנס''' אם סדרת הסכומים החלקיים <math>S^{a_n}</math> מתכנסת. (במובן הגדרת הגבול של סדרות, כמובן) | + | *אומרים כי טור הסדרה <math>a_n</math> '''מתכנס''' אם סדרת הסכומים החלקיים <math>S^{a_n}</math> מתכנסת לגבול סופי. (במובן הגדרת הגבול של סדרות, כמובן) |
| − | + | **במקרה זה אומרים כי סכום הטור שווה לגבול סדרת הסכומים החלקיים. כלומר <math>\displaystyle\sum_{n=1}^\infty a_n=\lim_{N\to\infty}S_N^{a_n}</math> . | |
| − | **במקרה זה אומרים כי סכום הטור שווה לגבול סדרת הסכומים החלקיים | + | |
*אומרים כי טור הסדרה <math>a_n</math> '''מתכנס בהחלט''' אם טור הסדרה <math>|a_n|</math> מתכנס. | *אומרים כי טור הסדרה <math>a_n</math> '''מתכנס בהחלט''' אם טור הסדרה <math>|a_n|</math> מתכנס. | ||
| שורה 36: | שורה 27: | ||
*אומרים כי טור '''מתכנס בתנאי''' אם הוא מתכנס, אך אינו מתכנס בהחלט. | *אומרים כי טור '''מתכנס בתנאי''' אם הוא מתכנס, אך אינו מתכנס בהחלט. | ||
| + | מסמנים את טור הסדרה <math>\displaystyle\sum_{n=1}^\infty a_n</math> . | ||
| − | |||
| + | <font size=4 color=#a7adcd>'''דוגמא חשובה.'''</font> | ||
| − | < | + | נחשב את סכום הטור <math>\displaystyle\sum_{n=0}^\infty x^n</math> |
| − | + | ||
| − | </ | + | |
| − | + | :<math>\begin{align}S_1&=x^0=1\\S_2&=x^0+x^1=1+x\\\vdots\\S_N&=1+x+x^2+\cdots+x^{N-1}\end{align}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
כעת, לפי הנוסחא לסכום סדרה הנדסית, מקבלים | כעת, לפי הנוסחא לסכום סדרה הנדסית, מקבלים | ||
| − | + | :<math>S_N=\dfrac{1-x^N}{1-x}</math> | |
| − | + | אם כך, <math>\displaystyle\sum_{n=0}^\infty x^n=\lim_{N\to\infty}S_N=\lim_{N\to\infty}\frac{1-x^N}{1-x}</math> | |
| − | אם כך, <math>\sum_{n=0}^\infty x^n=\lim_{N\ | + | |
זה תרגיל בסדרות, וקל לראות כי: | זה תרגיל בסדרות, וקל לראות כי: | ||
| − | + | :אם <math>|x|<1</math> הסדרה מתכנסת ומקבלים <math>\displaystyle\sum_{n=0}^\infty x^n=\frac1{1-x}</math> | |
| − | + | :אם <math>x=1</math> הסדרה לא מוגדרת, כיון שאסור היה להשתמש בנוסחת הסכום במקרה זה. קל לראות, אמנם, כי סדרת הסכומים החלקיים האמיתית היא <math>S_N=N</math> וכיון שהיא שואפת לאינסוף, הטור מתבדר. | |
| − | + | :אם <math>x=-1</math> הסדרה מתבדרת וכך גם הטור | |
| − | + | :אם <math>|x|>1</math> הסדרת אינה חסומה, ולכן מתבדרת ולכן הטור מתבדר. | |
| + | '''שימו לב:''' אם נתחיל את הספירה ממקום אחר, נקבל סכום אחר. <math>\displaystyle\sum_{n=1}^\infty x^n=\frac{x}{1-x}</math> . אם כך, '''מספר סופי של אברים לא משפיע על התכנסות הטור, אך עשוי להשפיע על סכומו'''. | ||
| − | |||
| + | באופן כללי, סדרת הסכומים החלקיים של טור מוגדרת על-ידי כלל הנסיגה <math>S_{N+1}^{a_n}=S^{a_n}_N+a_{N+1}</math> . | ||
| + | <font size=4 color=#a7adcd>'''דוגמא חשובה.'''</font> | ||
| + | ניזכר בתרגילים מ[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/קושי|סדרות קושי]]. נשים לב כי סדרת הסכומים החלקיים של הטור <math>\displaystyle\sum_{n=1}^\infty\frac1n</math> (הנקרא לעתים הטור '''ההרמוני''') מוגדרת על ידי כלל הנסיגה <math>S_{N+1}=S_N+\dfrac1{n+1}</math> . כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר. | ||
| − | באופן | + | באופן דומה, נסיק כי הטור <math>\displaystyle\sum_{n=1}^\infty\frac1{n^2}</math> מתכנס. |
| − | < | + | באופן כללי, הטור <math>\displaystyle\sum_{n=1}^\infty\frac1{n^\alpha}</math> מתכנס אם"ם <math>\alpha>1</math> אבל את זה נלמד בהמשך. |
| − | + | ||
| − | </ | + | |
| − | + | ==הקשר בין התכנסות טור לבין גבול הסדרה של הטור== | |
| + | אם <math>\displaystyle\sum_{n=1}^\infty a_n</math> מתכנס אזי בהכרח <math>\lim\limits_{n\to\infty}a_n=0</math> | ||
| − | + | '''הכיוון ההפוך אינו נכון בהכרח!!!!''' | |
| − | + | לדוגמא, <math>\lim\limits_{n\to\infty}\dfrac1n=0</math> ואילו הטור <math>\displaystyle\sum_{n=1}^\infty\frac1n</math> אינו מתכנס. | |
| − | == | + | ==טורים טלסקופיים== |
| + | כפי שטלסקופ ארוך מאד (או אנטנה של רדיו) מתקפלים אל תוך עצמם (כל חתיכה נכנסת בקודמה), כך לעתים סכום של מספרים מתבטל ברובו ומשאיר רק מספר קטן של מחוברים. אם תרצו, זהו טור מטריושקה. | ||
| − | + | לדוגמא, קל לוודא כי <math>\displaystyle\sum_{n=1}^{10}\frac1n-\frac1{n+1}=\frac11-\frac12+\frac12-\frac13+\cdots=\frac11-\frac1{11}</math> | |
| − | ''' | + | טור נקרא '''טלסקופי''' אם סדרת הסכומים החלקיים שלו מצטמצמת באופן דומה לדוגמא לעיל. זו אינה הגדרה מתמטית מדויקת, אלא כינוי לדרך מסוימת לחשב סכום של טור. |
| − | |||
| + | <font size=4 color=#a7adcd>'''תרגיל.'''</font> | ||
| − | + | הוכח כי הטור הבא מתכנס ומצא את סכומו | |
| − | + | ||
| − | + | :<math>\displaystyle\sum_{n=1}^\infty\frac1{(n+2)(n+4)}</math> | |
| + | ;פתרון. | ||
| + | נפרק את הביטוי לשברים חלקיים, על-מנת לקבל <math>\dfrac1{(n+2)(n+4)}=\dfrac1{2(n+2)}-\dfrac1{2(n+4)}</math> | ||
| − | + | על-ידי התבוננות במספר האיברים הראשונים של הטור, אנו מנחשים כי סדרת הסכומים החלקיים מקיימת את הנוסחא | |
| + | :<math>S_N=\dfrac16+\dfrac18-\dfrac1{2n+6}-\dfrac1{2n+8}</math> | ||
| − | + | את נוסחא זו קל להוכיח באינדוקציה. | |
| − | + | ||
| − | + | ||
| − | + | אם כך, סכום הטור - הלא הוא גבול סדרת הסכומים החלקיים - שווה <math>\lim\limits_{N\to\infty}S_N=\dfrac16+\dfrac18=\dfrac7{24}</math> | |
| − | |||
| − | ''' | + | <font size=4 color=#a7adcd>'''תרגיל.'''</font> |
| + | קבע אם הטור הבא מתכנס | ||
| + | :<math>\displaystyle\sum_{n=1}^\infty\ln\left(\frac{n+1}{n}\right)</math> | ||
| − | + | ;פתרון. | |
| − | + | נביט בסדרת הסכומים החלקיים | |
| − | + | :<math>\begin{align}S_N&=\ln\left(\dfrac21\right)+\cdots+\ln\left(\dfrac{N+1}{N}\right)\\S_N&=\ln(2)-\ln(1)+\ln(3)-\ln(2)+\cdots+\ln(N+1)-\ln(N)\\&=\ln(N+1)-\ln(1)=\ln(N+1)\end{align}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ולכן סדרת הסכומים החלקיים שואפת לאינסוף והטור אינו מתכנס. | |
גרסה אחרונה מ־06:43, 14 בפברואר 2017
הגדרות בסיסיות של טורים
באופן בלתי פורמלי, טור הנו סכום אינסופי של מספרים. נשאלת השאלה, האם סכום אינסופי של מספרים חיוביים עשוי להיות קטן ממספר סופי?
נענת התשובה - כן. לדוגמא, ניקח עוגה (או פאי). נחלק חצי מהעוגה לתלמיד המצטיין, חצי ממה שנשאר (רבע) ניתן לתלמיד הבא אחריו. חצי ממה שנשאר (שמינית) ניתן לתלמיד הבא אחריו. אחד חלקי שש עשרה יקבל התלמיד הבא וכן הלאה.
כמובן שלא נוכל לחלק יותר מאשר עוגה אחת ממנה התחלנו. לכן, אינטואיטיבית, 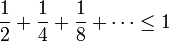
הגדרה.
נגדיר את סדרת הסכומים החלקיים 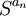 של סדרה
של סדרה  כלשהי להיות
כלשהי להיות 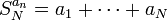 .
.
כלומר,
וכן הלאה.
הגדרה.
- אומרים כי טור הסדרה
 מתכנס אם סדרת הסכומים החלקיים
מתכנס אם סדרת הסכומים החלקיים 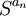 מתכנסת לגבול סופי. (במובן הגדרת הגבול של סדרות, כמובן)
מתכנסת לגבול סופי. (במובן הגדרת הגבול של סדרות, כמובן)
- במקרה זה אומרים כי סכום הטור שווה לגבול סדרת הסכומים החלקיים. כלומר
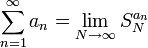 .
.
- במקרה זה אומרים כי סכום הטור שווה לגבול סדרת הסכומים החלקיים. כלומר
- אומרים כי טור הסדרה
 מתכנס בהחלט אם טור הסדרה
מתכנס בהחלט אם טור הסדרה 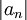 מתכנס.
מתכנס.
- אומרים כי טור מתכנס בתנאי אם הוא מתכנס, אך אינו מתכנס בהחלט.
מסמנים את טור הסדרה 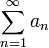 .
.
דוגמא חשובה.
נחשב את סכום הטור 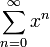
כעת, לפי הנוסחא לסכום סדרה הנדסית, מקבלים
אם כך, 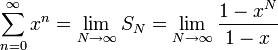
זה תרגיל בסדרות, וקל לראות כי:
- אם
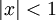 הסדרה מתכנסת ומקבלים
הסדרה מתכנסת ומקבלים 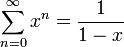
- אם
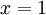 הסדרה לא מוגדרת, כיון שאסור היה להשתמש בנוסחת הסכום במקרה זה. קל לראות, אמנם, כי סדרת הסכומים החלקיים האמיתית היא
הסדרה לא מוגדרת, כיון שאסור היה להשתמש בנוסחת הסכום במקרה זה. קל לראות, אמנם, כי סדרת הסכומים החלקיים האמיתית היא 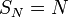 וכיון שהיא שואפת לאינסוף, הטור מתבדר.
וכיון שהיא שואפת לאינסוף, הטור מתבדר.
- אם
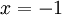 הסדרה מתבדרת וכך גם הטור
הסדרה מתבדרת וכך גם הטור
- אם
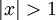 הסדרת אינה חסומה, ולכן מתבדרת ולכן הטור מתבדר.
הסדרת אינה חסומה, ולכן מתבדרת ולכן הטור מתבדר.
שימו לב: אם נתחיל את הספירה ממקום אחר, נקבל סכום אחר. 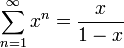 . אם כך, מספר סופי של אברים לא משפיע על התכנסות הטור, אך עשוי להשפיע על סכומו.
. אם כך, מספר סופי של אברים לא משפיע על התכנסות הטור, אך עשוי להשפיע על סכומו.
באופן כללי, סדרת הסכומים החלקיים של טור מוגדרת על-ידי כלל הנסיגה 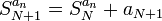 .
.
דוגמא חשובה.
ניזכר בתרגילים מסדרות קושי. נשים לב כי סדרת הסכומים החלקיים של הטור 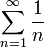 (הנקרא לעתים הטור ההרמוני) מוגדרת על ידי כלל הנסיגה
(הנקרא לעתים הטור ההרמוני) מוגדרת על ידי כלל הנסיגה 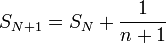 . כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר.
. כפי שראינו, סדרה זו אינה סדרת קושי ולכן מתבדרת, ולכן הטור ההרמוני מתבדר.
באופן דומה, נסיק כי הטור 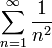 מתכנס.
מתכנס.
באופן כללי, הטור 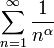 מתכנס אם"ם
מתכנס אם"ם 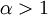 אבל את זה נלמד בהמשך.
אבל את זה נלמד בהמשך.
הקשר בין התכנסות טור לבין גבול הסדרה של הטור
אם 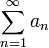 מתכנס אזי בהכרח
מתכנס אזי בהכרח 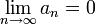
הכיוון ההפוך אינו נכון בהכרח!!!!
לדוגמא, 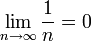 ואילו הטור
ואילו הטור 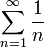 אינו מתכנס.
אינו מתכנס.
טורים טלסקופיים
כפי שטלסקופ ארוך מאד (או אנטנה של רדיו) מתקפלים אל תוך עצמם (כל חתיכה נכנסת בקודמה), כך לעתים סכום של מספרים מתבטל ברובו ומשאיר רק מספר קטן של מחוברים. אם תרצו, זהו טור מטריושקה.
לדוגמא, קל לוודא כי 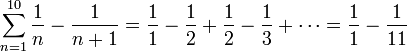
טור נקרא טלסקופי אם סדרת הסכומים החלקיים שלו מצטמצמת באופן דומה לדוגמא לעיל. זו אינה הגדרה מתמטית מדויקת, אלא כינוי לדרך מסוימת לחשב סכום של טור.
תרגיל.
הוכח כי הטור הבא מתכנס ומצא את סכומו
- פתרון.
נפרק את הביטוי לשברים חלקיים, על-מנת לקבל 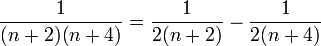
על-ידי התבוננות במספר האיברים הראשונים של הטור, אנו מנחשים כי סדרת הסכומים החלקיים מקיימת את הנוסחא
את נוסחא זו קל להוכיח באינדוקציה.
אם כך, סכום הטור - הלא הוא גבול סדרת הסכומים החלקיים - שווה 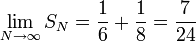
תרגיל.
קבע אם הטור הבא מתכנס
- פתרון.
נביט בסדרת הסכומים החלקיים
ולכן סדרת הסכומים החלקיים שואפת לאינסוף והטור אינו מתכנס.