הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/2"
מתוך Math-Wiki
(תיקון) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | [[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | ||
| − | + | *<math>\displaystyle\sum_{n=1}^\infty\frac{\sqrt[m]{n!}}{\sqrt[k]{(2n)!}}</math> , כאשר <math>m,k\in\N</math> | |
| − | *<math>\ | + | |
| − | + | ||
נפעיל את '''מבחן המנה (דלאמבר)''': | נפעיל את '''מבחן המנה (דלאמבר)''': | ||
| + | :<math>\displaystyle\begin{align}\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\lim_{n\to\infty}\frac{\sqrt[m]{(n+1)!}}{\sqrt[k]{(2(n+1))!}}\cdot\frac{\sqrt[k]{(2n)!}}{\sqrt[m]{n!}}=\lim_{n\to\infty}\frac{\sqrt[m]{n+1}}{\sqrt[k]{(2n+1)(2n+2)}}=\lim_{n\to\infty}\frac{\sqrt[m]{n}}{\sqrt[k]{4n^2}}\cdot | ||
| + | \frac{\sqrt[m]{1+\frac1n}}{\sqrt[k]{1+\frac3{2n}+\frac1{2n^2}}}\end{align}</math> | ||
| − | + | הביטוי הימני שואף ל-1, לכן מספיק לנו לחשב את הגבול: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | הביטוי הימני שואף | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | :<math>\lim_{n\to\infty}\dfrac{\sqrt[m]n}{\sqrt[k]{4n^2}}=\dfrac{n^{\frac1m-\frac2k}}{\sqrt[k]4}</math> | |
| − | + | '''נחלק למקרים:''' | |
| + | :<math>\dfrac1m-\dfrac2k>0</math> (כלומר <math>2m<k</math>) | ||
| − | <math>\lim \ | + | אזי <math>\lim\limits_{n\to\infty}\dfrac{a_{n+1}}{a_n}=\infty</math> והטור '''מתבדר''' |
| + | :<math>\dfrac1m-\dfrac2k<0</math> (כלומר <math>2m>k</math>) | ||
| − | + | אזי <math>\lim\limits_{n\to\infty}\dfrac{a_{n+1}}{a_n}=0</math> והטור '''מתכנס''' | |
| − | + | :<math>\frac1m-\frac2k=0</math> (כלומר <math>2m=k</math>) | |
| − | לכל k | + | אזי לכל <math>k</math> מתקיים <math>\lim\limits_{n\to\infty}\frac{a_{n+1}}{a_n}=\frac1{\sqrt[k]4}<1</math> ולכן הטור '''מתכנס'''. |
גרסה אחרונה מ־23:56, 14 בפברואר 2017
![\displaystyle\sum_{n=1}^\infty\frac{\sqrt[m]{n!}}{\sqrt[k]{(2n)!}}](/images/math/1/e/5/1e5f13f615ec5b21b99af1b7e9e0a712.png) , כאשר
, כאשר 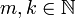
נפעיל את מבחן המנה (דלאמבר):
הביטוי הימני שואף ל-1, לכן מספיק לנו לחשב את הגבול:
נחלק למקרים:
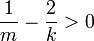 (כלומר
(כלומר 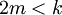 )
)
אזי 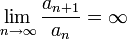 והטור מתבדר
והטור מתבדר
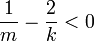 (כלומר
(כלומר 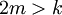 )
)
אזי 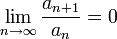 והטור מתכנס
והטור מתכנס
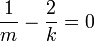 (כלומר
(כלומר 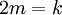 )
)
אזי לכל  מתקיים
מתקיים ![\lim\limits_{n\to\infty}\frac{a_{n+1}}{a_n}=\frac1{\sqrt[k]4}<1](/images/math/3/3/8/33840b6d0465b0191313d6ba38dcd46a.png) ולכן הטור מתכנס.
ולכן הטור מתכנס.
![\displaystyle\begin{align}\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\lim_{n\to\infty}\frac{\sqrt[m]{(n+1)!}}{\sqrt[k]{(2(n+1))!}}\cdot\frac{\sqrt[k]{(2n)!}}{\sqrt[m]{n!}}=\lim_{n\to\infty}\frac{\sqrt[m]{n+1}}{\sqrt[k]{(2n+1)(2n+2)}}=\lim_{n\to\infty}\frac{\sqrt[m]{n}}{\sqrt[k]{4n^2}}\cdot
\frac{\sqrt[m]{1+\frac1n}}{\sqrt[k]{1+\frac3{2n}+\frac1{2n^2}}}\end{align}](/images/math/a/7/9/a79445568b4b9111b7a975285a40abb3.png)
![\lim_{n\to\infty}\dfrac{\sqrt[m]n}{\sqrt[k]{4n^2}}=\dfrac{n^{\frac1m-\frac2k}}{\sqrt[k]4}](/images/math/3/b/0/3b03e8f5246a09bc11c93179fa7c75b6.png)