הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/3"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) |
|||
| שורה 1: | שורה 1: | ||
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | [[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | ||
| − | *<math>\ | + | *<math>\displaystyle\sum_{n=1}^\infty\frac1{\sqrt[n]{(n!)^2}}</math> |
| − | + | ;פתרון. | |
| + | [[המספר e#דוגמאות|נשים לב]] כי <math>\lim\limits_{n\to\infty}\dfrac{n}{\sqrt[n]{n!}}=e</math> | ||
| − | + | ולכן <math>\lim\limits_{n\to\infty}\dfrac{n^2}{\sqrt[n]{n!}^2}=e^2</math> | |
| − | ולכן <math>\ | + | ולכן הטור חבר של <math>\displaystyle\sum_{n=1}^\infty\frac1{n^2}</math> ולכן מתכנס. |
| − | + | ;פתרון ישן | |
| + | נשים לב כי לפחות '''שני שלישים''' מאברי המכפלה <math>1\cdot2\cdot3\cdots n</math> גדולים מהמספר <math>\frac{n}{3}</math> . | ||
| + | נקטין את כל האברים במכפלה שגדולים מ- <math>\frac{n}{3}</math>, ומכיוון שיש לפחות <math>\frac23n</math> כאלה נקבל ש- | ||
| + | <math>n!=1\cdot2\cdots\left\lfloor\frac{n}{3}\right\rfloor\cdot\left(\left\lfloor\frac{n}{3}\right\rfloor+1\right)\cdots n\ge1\cdot2\cdots\left\lfloor\frac{n}{3}\right\rfloor\cdot\left(\frac{n}{3}\right)^{\frac23n}</math> | ||
| − | + | (נניח <math>n>2</math> , קל לבדוק את <math>n=1,2</math>) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | (נניח <math>n>2</math>, קל לבדוק את <math>n=1,2</math>) | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | נעלה בריבוע ונקבל כי | ||
| + | :<math>(n!)^2\ge\left(\frac{n}{3}\right)^\frac{4n}{3}</math> | ||
ולכן | ולכן | ||
| − | + | :<math>\dfrac1{\sqrt[n]{(n!)^2}}\le\dfrac1{\sqrt[n]{\left(\frac{n}{3}\right)^\frac{4n}{3}}}</math> | |
| − | + | ||
אבל קל לראות כי הטורים הבאים חברים (לפי '''מבחן ההשוואה הגבולי''') | אבל קל לראות כי הטורים הבאים חברים (לפי '''מבחן ההשוואה הגבולי''') | ||
| − | + | :<math>\displaystyle\sum_{n=1}^\infty\frac1{\sqrt[n]{\left(\frac{n}{3}\right)^\frac{4n}{3}}}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | :<math>\displaystyle\sum_{n=1}^\infty\frac1{n^\frac43}</math> (ידוע כי טור זה מתכנס) | ||
וביחד הטור '''מתכנס''' לפי '''מבחן ההשוואה הראשון'''. | וביחד הטור '''מתכנס''' לפי '''מבחן ההשוואה הראשון'''. | ||
גרסה אחרונה מ־00:06, 15 בפברואר 2017
- פתרון.
נשים לב כי ![\lim\limits_{n\to\infty}\dfrac{n}{\sqrt[n]{n!}}=e](/images/math/3/9/8/398dee184bf536871c7a41311174c4ff.png)
ולכן ![\lim\limits_{n\to\infty}\dfrac{n^2}{\sqrt[n]{n!}^2}=e^2](/images/math/8/4/6/8469298688a73bc1e8bfcfb1db1bea6b.png)
ולכן הטור חבר של 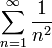 ולכן מתכנס.
ולכן מתכנס.
- פתרון ישן
נשים לב כי לפחות שני שלישים מאברי המכפלה 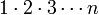 גדולים מהמספר
גדולים מהמספר 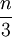 .
.
נקטין את כל האברים במכפלה שגדולים מ- 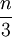 , ומכיוון שיש לפחות
, ומכיוון שיש לפחות 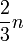 כאלה נקבל ש-
כאלה נקבל ש-
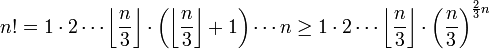
(נניח 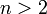 , קל לבדוק את
, קל לבדוק את 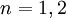 )
)
נעלה בריבוע ונקבל כי
ולכן
אבל קל לראות כי הטורים הבאים חברים (לפי מבחן ההשוואה הגבולי)
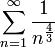 (ידוע כי טור זה מתכנס)
(ידוע כי טור זה מתכנס)
וביחד הטור מתכנס לפי מבחן ההשוואה הראשון.
![\displaystyle\sum_{n=1}^\infty\frac1{\sqrt[n]{(n!)^2}}](/images/math/c/b/0/cb0a059a3ca7d20d3c3f9e1934eb7fa1.png)
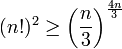
![\dfrac1{\sqrt[n]{(n!)^2}}\le\dfrac1{\sqrt[n]{\left(\frac{n}{3}\right)^\frac{4n}{3}}}](/images/math/e/e/e/eeeb32ecfe6e1e5a1fdf2c842ad2e4be.png)
![\displaystyle\sum_{n=1}^\infty\frac1{\sqrt[n]{\left(\frac{n}{3}\right)^\frac{4n}{3}}}](/images/math/2/3/6/2360322f23636599e8f2432f12c72b3b.png)