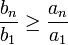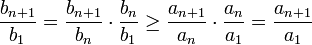הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/5"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) |
|||
| שורה 1: | שורה 1: | ||
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | [[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות|חזרה לדוגמאות]] | ||
| + | *יהיו <math>\displaystyle\sum_{n=1}^\infty a_n,\sum_{n=1}^\infty b_n</math> טורים חיוביים כך ש- <math>\dfrac{a_{n+1}}{a_n}\le\dfrac{b_{n+1}}{b_n}</math> . | ||
| + | הוכיחו כי אם <math>\displaystyle\sum_{n=1}^\infty b_n</math> מתכנס אזי גם <math>\displaystyle\sum_{n=1}^\infty a_n</math> מתכנס | ||
| + | ;הוכחה. | ||
| + | אנו רואים מהנתון שקצב הגדילה של הטור <math>b_n</math> גדול מזה של <math>a_n</math> , ואנו יודעים שכפל על-ידי קבוע שונה מ-0 אינו משנה את התכנסות הטור. לכן נכפול בקבוע כך שהטורים יתחילו שניהם באבר ששוה ל-1, ונקבל שהטור <math>b_n</math> גדול מהטור <math>a_n</math> : | ||
| − | + | :<math>\displaystyle\sum_{n=1}^\infty\frac{b_n}{b_1}</math> מתכנס. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
צריך להוכיח כי | צריך להוכיח כי | ||
| − | + | :<math>\displaystyle\sum_{n=1}^\infty\frac{a_n}{a_1}</math> מתכנס. | |
| − | + | ||
| − | + | ||
| − | + | ||
אבל קל להוכיח באינדוקציה כי | אבל קל להוכיח באינדוקציה כי | ||
| − | + | :<math>\dfrac{b_n}{b_1}\ge\dfrac{a_n}{a_1}</math> | |
| − | + | ||
| − | + | ||
אכן, | אכן, | ||
| + | :<math>\dfrac{b_{n+1}}{b_1}=\dfrac{b_{n+1}}{b_n}\cdot\dfrac{b_n}{b_1}\ge\dfrac{a_{n+1}}{a_n}\cdot\dfrac{a_n}{a_1}=\dfrac{a_{n+1}}{a_1}</math> | ||
| − | + | (את הנחת האינדוקציה קיבלנו בזכות הכפל בקבוע, שכן <math>\dfrac{a_1}{a_1}=\dfrac{b_1}{b_1}</math>) | |
| − | + | ||
| − | + | ||
| − | (את הנחת האינדוקציה קיבלנו בזכות הכפל בקבוע, שכן <math>\ | + | |
| − | + | ||
| − | + | ||
| − | ולכן לפי '''מבחן ההשוואה הראשון''' אנו מקבלים את | + | ולכן לפי '''מבחן ההשוואה הראשון''' אנו מקבלים את שרצינו. |
גרסה אחרונה מ־13:06, 15 בפברואר 2017
- יהיו
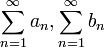 טורים חיוביים כך ש-
טורים חיוביים כך ש- 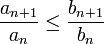 .
.
הוכיחו כי אם 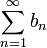 מתכנס אזי גם
מתכנס אזי גם 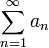 מתכנס
מתכנס
- הוכחה.
אנו רואים מהנתון שקצב הגדילה של הטור  גדול מזה של
גדול מזה של  , ואנו יודעים שכפל על-ידי קבוע שונה מ-0 אינו משנה את התכנסות הטור. לכן נכפול בקבוע כך שהטורים יתחילו שניהם באבר ששוה ל-1, ונקבל שהטור
, ואנו יודעים שכפל על-ידי קבוע שונה מ-0 אינו משנה את התכנסות הטור. לכן נכפול בקבוע כך שהטורים יתחילו שניהם באבר ששוה ל-1, ונקבל שהטור  גדול מהטור
גדול מהטור  :
:
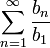 מתכנס.
מתכנס.
צריך להוכיח כי
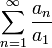 מתכנס.
מתכנס.
אבל קל להוכיח באינדוקציה כי
אכן,
(את הנחת האינדוקציה קיבלנו בזכות הכפל בקבוע, שכן 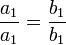 )
)
ולכן לפי מבחן ההשוואה הראשון אנו מקבלים את שרצינו.