הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/גבול"
(←אי שוויון הממוצעים) |
(←אריתמטיקה (חשבון) של גבולות) |
||
| שורה 160: | שורה 160: | ||
'''תרגיל חשוב מאד.''' | '''תרגיל חשוב מאד.''' | ||
</font> | </font> | ||
| − | תהי סדרה <math>a_n\rightarrow 0</math> ותהי <math>b_n</math> סדרה '''חסומה'''. (כלומר, קיים M כך שלכל מקום בסדרה n מתקיים <math>| | + | תהי סדרה <math>a_n\rightarrow 0</math> ותהי <math>b_n</math> סדרה '''חסומה'''. (כלומר, קיים M כך שלכל מקום בסדרה n מתקיים <math>|b_n|<M</math>. ישנם אינסוף מספרים בסדרה, אבל קבוצת האיברים שנמצאים בסדרה חסומה מלעיל ומלרע). |
:הוכח: <math>a_nb_n\rightarrow 0</math> | :הוכח: <math>a_nb_n\rightarrow 0</math> | ||
גרסה מ־17:01, 17 בדצמבר 2011
תוכן עניינים
גבול של סדרה
ההגדרה המדוייקת של סדרה
הגדרה. בבדידה נלמד/למדנו את ההגדרה המדוייקת של פונקציה. סדרה הינה פונקציה מקבוצת הטבעיים אל קבוצה כלשהי. סדרה ממשית, למשל, הינה פונקציה מהטבעיים אל הממשיים.
באופן טבעי, התמונה של המספר הטבעי 1 נקראת האיבר הראשון של הסדרה, התמונה של 2 היא האיבר השני וכן הלאה.
גבול של סדרה
תהי סדרת מספרים ממשיים 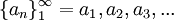 , (כך ש
, (כך ש 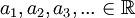 ).
).
לדוגמא:
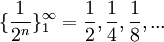
גבול של סדרה הוא נקודה ממשית אליה איברי הסדרה מתקרבים. לסדרה שלא מתקרבת לנקודה ספציפית אין גבול, למשל: 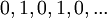 (לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
(לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
הגדרת הגבול
הגדרה.
תהי 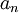 סדרה של מספרים ממשיים. אזי מספר ממשי
סדרה של מספרים ממשיים. אזי מספר ממשי 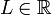 נקרא גבול הסדרה
נקרא גבול הסדרה 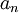 אם לכל
אם לכל 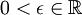 קיים
קיים 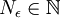 כך שלכל
כך שלכל 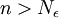 מתקיים
מתקיים 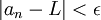 .
.
במקרה זה מסמנים 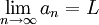
הסבר ההגדרה
נתרגם את זה למילים. למדנו ש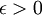 מודד אורך, מספר טבעי
מודד אורך, מספר טבעי 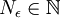 מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
נקודה L על ציר המספרים הממשיים היא גבול הסדרה 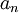
אם לכל אורך (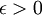 ) [סיר]
) [סיר]
קיים מקום בסדרה (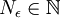 ) [מכסה]
) [מכסה]
כך שהחל ממנו והלאה (לכל 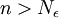 ) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך
) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך 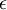 (
(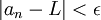 ) [מתאים לו]
) [מתאים לו]
דוגמאות
תרגיל.
מצא את גבול הסדרה 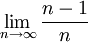
פתרון. מהתבוננות באיברים הראשונים של הסדרה אנו מנחשים שגבול הסדרה הינו 1. נוכיח זאת.
יהי אפסילון גדול מאפס. (הוכחה באינפי מתחילה בשורה זו לעיתים תכופות. מכיוון שההגדרות דורשות שתכונה מסוימת תתקיים לכל אפסילון, אם נוכיח אותה לאפסילון מבלי להתייחס לערך שלו, הוכחנו שהיא נכונה תמיד.)
כעת, אנו רוצים למצוא מקום בסדרה שהחל ממנו והלאה איברי הסדרה קרובים לאחד עד כדי אפסילון. כלומר:
נפתח את הביטוי.
כעת, אנו מעוניינים כי יתקיים 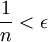 , זה נכון אם"ם
, זה נכון אם"ם 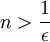
נבחר, אפוא, 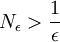 כלשהו (מותר כיוון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל
כלשהו (מותר כיוון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל 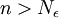 מתקיים
מתקיים 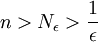 ולכן איברי הסדרה קרובים ל-1 עד כדי אפסילון כפי שרצינו.
ולכן איברי הסדרה קרובים ל-1 עד כדי אפסילון כפי שרצינו.
תרגיל.
הוכיחו לפי הגדרה כי מתקיים: 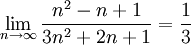
תרגיל.
מצא את גבול הסדרה ![a_n=\sqrt[n]{n}](/images/math/1/1/9/119681e74abf91474f594fb693206280.png)
ננחש את הגבול ע"י הצבה במחשבון (או אינטואיציה מבריקה) להיות אחד. כעת, יהי אפסילון כלשהו, נוכיח כי קיים מקום בסדרה החל ממנו איברי הסדרה קרובים לאחד עד כדי אפסילון. כלומר, 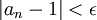 .
.
זה שקול ל- 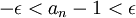
זה שקול ל- ![1-\epsilon<\sqrt[n]{n}<1+\epsilon](/images/math/3/6/0/3608eb62b90ac3bdf22581fcc4170960.png)
כיוון ש 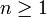 הצד השמאלי טריוויאלי (שכן אם השורש היה קטן מאחד, כאשר היינו מעלים אותו בחזקה הוא היה נשאר קטן מאחד). לכן נותר עלינו להוכיח כי קיים מקום בסדרה
הצד השמאלי טריוויאלי (שכן אם השורש היה קטן מאחד, כאשר היינו מעלים אותו בחזקה הוא היה נשאר קטן מאחד). לכן נותר עלינו להוכיח כי קיים מקום בסדרה 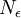 כך שלכל
כך שלכל 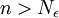 מתקיים
מתקיים ![\sqrt[n]{n}<1+\epsilon](/images/math/6/c/c/6cc21d88854c36f243450da5740d3648.png)
כלומר, אנו רוצים שיתקיים 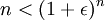
נביט בביטוי 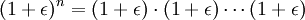 . נזכר בשיעור קומבינטוריקה ונשים לב שכמות האפשרויות לקבל אפסילון כפול אפסילון כפול אחדות בעת פתיחת הסוגריים שווה לכמות האפשרויות לבחור זוגות מבין n איברים והיא
. נזכר בשיעור קומבינטוריקה ונשים לב שכמות האפשרויות לקבל אפסילון כפול אפסילון כפול אחדות בעת פתיחת הסוגריים שווה לכמות האפשרויות לבחור זוגות מבין n איברים והיא 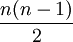 . בסה"כ אנו מקבלים:
. בסה"כ אנו מקבלים:
(כאשר K הוא מספר חיובי כלשהו המורכב משאר הכפולות שהשמטנו.)
אם כך, 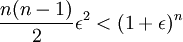 . לכן, אם נמצא מקום בסדרה שהחל ממנו מתקיים
. לכן, אם נמצא מקום בסדרה שהחל ממנו מתקיים 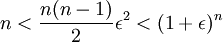 נסיים את התרגיל.
נסיים את התרגיל.
וכמובן שכיוון שהמספרים הטבעיים אינם חסומים, אחרי מקום מסויים בסדרה אי השיוויון הזה יתקיים כפי שרצינו.
אם כן, הוכחנו כי
שלילת גבול
שלילת הגבול.
- L אינו גבול של סדרה אם קיים
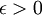 כך שלכל
כך שלכל 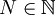 קיים
קיים 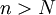 כך ש
כך ש 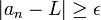
תרגיל.
הוכח שלסדרה 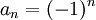 לא קיים גבול
לא קיים גבול
נניח בשלילה שקיים גבול L ממשי כלשהו. נניח עוד כי L אי שלילי (ההוכחה עבור השליליים תהא דומה). ניקח 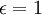 (הרי צריך להוכיח כי קיים אפסילון). כעת, יהי
(הרי צריך להוכיח כי קיים אפסילון). כעת, יהי 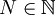 ניקח n אי זוגי גדול ממנו. במקרה זה
ניקח n אי זוגי גדול ממנו. במקרה זה 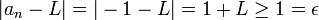 כפי שרצינו. (שימו לב שהורדנו את הערך המוחלט בעזרת ההנחה כי L אינו שלילי.)
כפי שרצינו. (שימו לב שהורדנו את הערך המוחלט בעזרת ההנחה כי L אינו שלילי.)
אריתמטיקה (חשבון) של גבולות
משפט. תהי 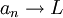 (סדרה השואפת לגבול L) ותהי
(סדרה השואפת לגבול L) ותהי 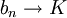 אזי:
אזי:
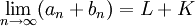
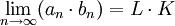
- אם
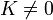 אזי
אזי 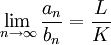
תרגיל.
מצא את גבול הסדרה 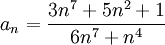 .
.
פתרון.
נחלק את המונה ואת המכנה ב- 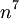 . נקבל
. נקבל 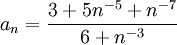 . חזקות שליליות של n שואפות לאפס ולכן לפי אריתמטיקה של גבולות אנו רואים כי הגבול שווה ל-
. חזקות שליליות של n שואפות לאפס ולכן לפי אריתמטיקה של גבולות אנו רואים כי הגבול שווה ל- 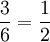 .
.
תרגיל.
נניח 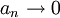 ולסדרה
ולסדרה 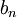 אין גבול. האם אנו יודעים לומר משהו על גבול הסדרה
אין גבול. האם אנו יודעים לומר משהו על גבול הסדרה 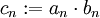 ?
?
תשובה: לא. כל האפשרויות מתקבלות:
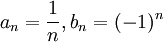 אזי
אזי
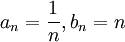 אזי
אזי
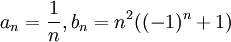 אזי
אזי
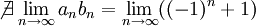 (לא קיים גבול לסדרה זו)
(לא קיים גבול לסדרה זו)
תרגיל חשוב מאד.
תהי סדרה 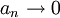 ותהי
ותהי 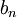 סדרה חסומה. (כלומר, קיים M כך שלכל מקום בסדרה n מתקיים
סדרה חסומה. (כלומר, קיים M כך שלכל מקום בסדרה n מתקיים 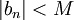 . ישנם אינסוף מספרים בסדרה, אבל קבוצת האיברים שנמצאים בסדרה חסומה מלעיל ומלרע).
. ישנם אינסוף מספרים בסדרה, אבל קבוצת האיברים שנמצאים בסדרה חסומה מלעיל ומלרע).
- הוכח:
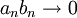
הוכחה.
יהי אפסילון גדול מאפס, צריך למצוא מקום בסדרה שהחל ממנו והלאה מתקיים 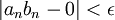
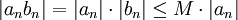 . מכיוון שידוע כי הסדרה
. מכיוון שידוע כי הסדרה 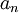 שואפת לאפס, יש מקום מסויים שהחל ממנו והלאה מתקיים
שואפת לאפס, יש מקום מסויים שהחל ממנו והלאה מתקיים 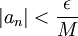 (כיוון ש
(כיוון ש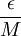 הינו מספר חיובי כלשהו, ולכל מספר חיובי קיים מקום בסדרה עבורו זה מתקיים, לפי הגדרת הגבול).
הינו מספר חיובי כלשהו, ולכל מספר חיובי קיים מקום בסדרה עבורו זה מתקיים, לפי הגדרת הגבול).
לכן, מאותו מקום מתקיים 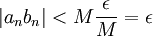 כפי שרצינו.
כפי שרצינו.
דוגמא.
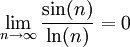
תרגיל.
מצא את הגבול 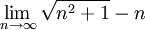
פתרון.
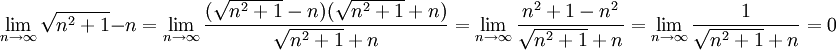
אי שוויון הממוצעים
כלי חשוב לפתרון תרגילים רבים הנו אי שוויון הממוצעים (אותו לא נוכיח בשלב זה):
לכל  מספרים ממשיים חיוביים
מספרים ממשיים חיוביים 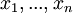 מתקיים:
מתקיים:
![\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}}\leq \sqrt[n]{x_1x_2....x_n} \leq \frac{x_1+x_2+...+x_n}{n}](/images/math/a/5/5/a55bd0f0e51a6612aa8e03fdb18cc0c1.png)
הביטוי מימין נקרא "ממוצע חשבוני", הביטוי האמצעי נקרא "ממוצע הנדסי" והביטוי השמאלי נקרא "ממוצע הרמוני".
טענה - אתם מוזמנים לנסות להוכיח אותה לבד!
אם 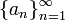 היא סדרת מספרים חיוביים המתכנסת לגבול
היא סדרת מספרים חיוביים המתכנסת לגבול 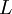 אזי מתקיים:
אזי מתקיים:
![\lim_{n\rightarrow \infty} \sqrt[n]{a_1a_2...a_n}=L](/images/math/5/e/e/5eeb51cd736f85a2a89fa027a294695d.png) .
.
משפט
תהי 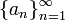 סדרת מספרים חיוביים. אם קיים הגבול
סדרת מספרים חיוביים. אם קיים הגבול 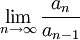 אזי הסדרה
אזי הסדרה ![\{\sqrt[n]{a_n} \}^\infty_{n=1}](/images/math/d/e/5/de52ca0a8f87fa6211b88033dffa6970.png) מתכנסת ומתקיים השוויון:
מתכנסת ומתקיים השוויון: ![\lim_{n\rightarrow \infty} \sqrt[n]{a_n}=\lim_{n\rightarrow \infty} \frac{a_n}{a_{n-1}}](/images/math/1/0/6/106a1957c6d8d93cee77fa7d07dc2110.png) .
.
הוכחה
נגדיר סדרה 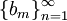 על ידי
על ידי 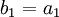 ו-
ו- 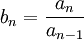 לכל
לכל 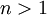 . זוהי סדרה של מספרים חיוביים ולכן על פי הטענה הקודמת מתקיים:
. זוהי סדרה של מספרים חיוביים ולכן על פי הטענה הקודמת מתקיים:
![\lim_{n\rightarrow \infty} \sqrt[n]{b_1b_2...b_n}=\lim_{n\rightarrow \infty} b_n=\lim_{n\rightarrow \infty} \frac{a_n}{a_{n-1}}](/images/math/e/1/b/e1b5cddcfb4a311bcf25037fadd29a01.png) .
.
ברור כי
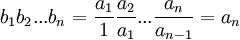
ולכן קיבלנו כי ![\lim_{n\rightarrow \infty} \sqrt[n]{a_n}=\lim_{n\rightarrow \infty}\frac{a_n}{a_{n-1}}](/images/math/1/0/6/106a1957c6d8d93cee77fa7d07dc2110.png) . מש"ל.
. מש"ל.
כעת נוכיח בדרך אחרת כי ![\lim_{n\rightarrow \infty} \sqrt[n]{n}=1](/images/math/9/0/3/903c5708320bb33d547a61fbde6df582.png) .
.
הוכחה
אם נרשום 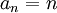 אזי לפי המשפט הקודם מתקיים:
אזי לפי המשפט הקודם מתקיים:
![\lim_{n\rightarrow \infty} \sqrt[n]{n}=\lim_{n\rightarrow \infty}\sqrt[n]{a_n}=\lim_{n\rightarrow \infty} \frac{a_n}{a_{n-1}}=\lim_{n\rightarrow \infty} \frac{n}{n-1}=1](/images/math/d/1/4/d1472f98aea9741fae0efc484f2e8064.png) . מש"ל.
. מש"ל.
חוק הסנדביץ'
הידוע גם בגרסא הרוסית חוק השוטרים והשיכור; לפיו אם שני שוטרים מובילים אדם שיכור בינהם ושני השוטרים מגיעים לתחנה, אזי גם השיכור (שאינו הולך ישר) יגיע איתם לתחנה. באופן דומה, אם מתקיים 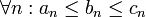 וגם ידוע כי
וגם ידוע כי 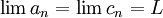 אזי בהכרח
אזי בהכרח 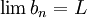
דוגמא.
מצא את גבול הסדרה 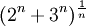
פתרון.
לכן,
כיוון שמתקיים
סה"כ שני צידי אי השיוויון מתכנסים ל-3 ואז לפי חוק הסנדביץ' גם הסדרה שלנו מתכנסת ל-3.
התכנסות במובן הרחב
דיברנו עד כה על התכנסות סדרה לגבול סופי מסויים. מה לגבי סדרות השואפות לאינסוף? אנו מעוניים להבדיל אותן מסדרות כפי שראינו לעיל שאינן מתקרבות לשום כיוון מסויים.
הגדרה.
תהא 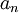 סדרה. אזי אומרים כי הסדרה מתכנסת במובן הרחב לאינסוף אם לכל
סדרה. אזי אומרים כי הסדרה מתכנסת במובן הרחב לאינסוף אם לכל 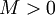 קיים
קיים 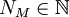 כך שלכל
כך שלכל 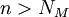 מתקיים
מתקיים 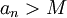
הערה: שימו לב ש-M בדומה לאפסילון מודד מרחק, אך מכיוון שההגבלה כאן היא חמורה יותר כאשר המרחק גדול (בניגוד לקטן) אנו מסמנים מרחק זה באות M ולא באות אפסילון. אנחנו נשמור על מתכונת זו לאורך הקורס.
ההגדרה להתכנסות במובן הרחב למינוס אינסוף דומה עם שינויים קלים בהתאם.
תרגיל.
מצא את גבול הסדרה ![a_n=\sqrt[n]{n!}](/images/math/0/0/8/0089796d8bd789eb91640ebfec4adee8.png)
פתרון. נוכיח כי סדרה זו מתכנסת במובן הרחב לאינסוף.
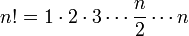 (המקרה בו n אינו זוגי מאד דומה אך דורש התעסקות עדינה יותר, לא נפרט לגביו).
(המקרה בו n אינו זוגי מאד דומה אך דורש התעסקות עדינה יותר, לא נפרט לגביו).
- נקטין את החצי הראשון של האיברים להיות 1, ואת החצי השני של האיברים להיות
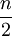 ונקבל:
ונקבל:
ולכן,
קל להוכיח שאם סדרה שואפת לאינסוף, סדרה הגדולה ממנה בכל איבר גם שואפת לאינסוף, כפי שרצינו.
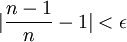
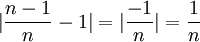
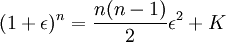
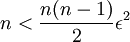
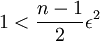
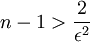
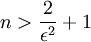
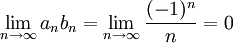
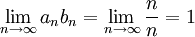
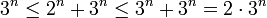
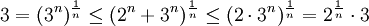
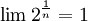
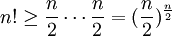
![\sqrt[n]{n!}\geq\sqrt[n]{(\frac{n}{2})^{\frac{n}{2}}}=\sqrt{\frac{n}{2}}\rightarrow\infty](/images/math/c/a/e/cae1c3ff55d19aa978a20967e37f2566.png)