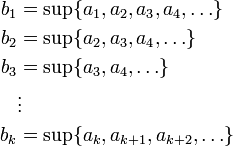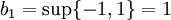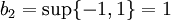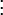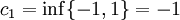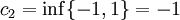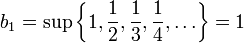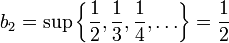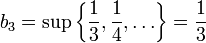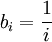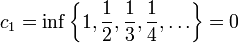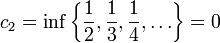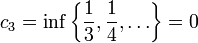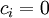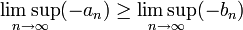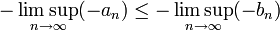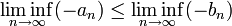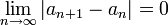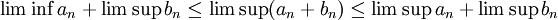הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/גבול עליון ותחתון"
יהודה שמחה (שיחה | תרומות) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 30: | שורה 30: | ||
;העשרה | ;העשרה | ||
| − | סדרה הנה פונקציה <math>a_n=a(n)</math> מהטבעיים לקבוצה A, כלומר יחס חד ערכי ושלם <math>a\subseteq\N\times A</math> . אם כך, אנו מגדירים | + | סדרה הנה פונקציה <math>a_n=a(n)</math> מהטבעיים לקבוצה <math>A</math> , כלומר יחס חד ערכי ושלם <math>a\subseteq\N\times A</math> . אם כך, אנו מגדירים |
| − | <math> | + | <math>b_k:=\sup\Big[im\big[a\cap(\N-\{1,2,\ldots,k-1\})\times A\big]\Big]</math> |
| − | + | ;<font size=4 color=#a7adcd>דוגמאות.</font> | |
| − | <font size=4 color=#a7adcd> | + | *נביט בסדרה <math>a_n=(-1)^n</math> . נבנה את סדרת החסמים <math>b_k</math> : |
| − | + | ||
| − | *נביט בסדרה <math>a_n=(-1)^n</math>. נבנה את סדרת החסמים <math> | + | |
| − | + | ||
:<math>b_1=\sup\{-1,1\}=1</math> | :<math>b_1=\sup\{-1,1\}=1</math> | ||
:<math>b_2=\sup\{-1,1\}=1</math> | :<math>b_2=\sup\{-1,1\}=1</math> | ||
גרסה אחרונה מ־12:04, 16 בפברואר 2017
גבול עליון וגבול תחתון
למדנו על חסמים על-מנת לחסום את הקבוצה באופן אידיאלי, כלומר למצוא את "קצות" הקבוצה. היינו רוצים למצוא הגדרה דומה עבור סדרות. השיטה התמימה היא להביט בחסמים של קבוצת אברי הסדרה, אך מהדוגמא הקלה הבאה נראה כי החסמים של קבוצת אברי הסדרה לא אומרים שום דבר על הסדרה:
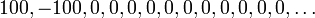
החסמים הם פלוס מינוס מאה, אך אין קשר בין מספרים אלה להתנהגות הסדרה באינסוף.
- הגדרה.
נגדיר
כלומר, אנו לוקחים את החסם העליון של קבוצת אברי הסדרה, אבל כל פעם אנחנו זורקים את האבר הבא מהסדרה. באופן טבעי, החסם העליון לא יגדל לאחר שנזרוק אבר.
אם כך, סדרת החסמים 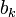 מונוטונית יורדת ולכן שואפת למספר כלשהו או למינוס אינסוף. אם הסדרה חסומה, לפי תרגיל מתקיים
מונוטונית יורדת ולכן שואפת למספר כלשהו או למינוס אינסוף. אם הסדרה חסומה, לפי תרגיל מתקיים 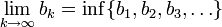
נגדיר את הגבול העליון של הסדרה  להיות
להיות
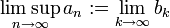
במילים בלתי-מדויקות, הגבול העליון הוא החסם העליון "באינסוף".
באופן דומה, הגבול התחתון הנו גבול החסמים התחתונים של קבוצות אברי הסדרה.
- העשרה
סדרה הנה פונקציה 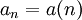 מהטבעיים לקבוצה
מהטבעיים לקבוצה  , כלומר יחס חד ערכי ושלם
, כלומר יחס חד ערכי ושלם 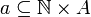 . אם כך, אנו מגדירים
. אם כך, אנו מגדירים
![b_k:=\sup\Big[im\big[a\cap(\N-\{1,2,\ldots,k-1\})\times A\big]\Big]](/images/math/6/a/5/6a5b1441097a5eac3001213dcffc929c.png)
- דוגמאות.
- נביט בסדרה
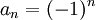 . נבנה את סדרת החסמים
. נבנה את סדרת החסמים 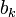 :
:
ולכן הגבול העליון הנו 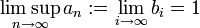
נביט כעת בסדרת החסמים 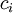 :
:
ולכן הגבול התחתון הנו 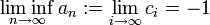
- נביט בסדרה
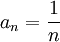 .
.
ולכן הגבול העליון הנו 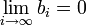
ולכן הגבול התחתון הנו 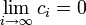
הקשר בין גבול עליון וגבול תחתון להתכנסות סדרות ותתי סדרות
משפט. לכל סדרה יש תת-סדרה המתכנסת לגבול העליון שלה, ותת סדרה המתכנסת לגבול התחתון שלה.
לכן הגבול העליון הוא מקסימום מקבוצת הגבולות החלקיים, והגבול התחתון הוא מינימום מקבוצת הגבולות החלקיים.
משפט. גבול סדרה שווה L אם"ם הגבול העליון של הסדרה שווה לגבול התחתון של הסדרה שווה ל-L.
תרגיל.
יהיו 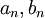 סדרות כך ש-
סדרות כך ש- 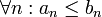 . הוכח/הפרך:
. הוכח/הפרך:
1. 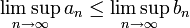
2. 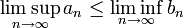
3. 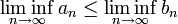
- פתרון
1. הוכחה:
- לפי המשפט קיימת תת סדרה המתכנסת לגבול העליון
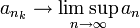
- לפי הנתון
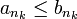
- לתת הסדרה
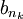 קיימת תת-סדרה השואפת לגבול העליון
קיימת תת-סדרה השואפת לגבול העליון 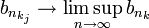
- כל תת סדרה של סדרה מתכנסת שואפת לגבול הסדרה, ולכן
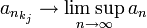
- מכיון ש
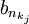 תת-סדרה של
תת-סדרה של  אזי הגבול שלה הוא גבול חלקי של
אזי הגבול שלה הוא גבול חלקי של  .
.
- כלומר,
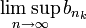 הנו גבול חלקי של
הנו גבול חלקי של  .
.
- כלומר,
- הגבול החלקי העליון של סדרה הוא הגבול החלקי הכי גדול שלה, ולכן מתקיים
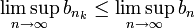
- כמו כן, כיון ש-
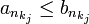 , הגבולות מקיימים את אותו היחס:
, הגבולות מקיימים את אותו היחס:
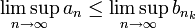
ביחד אנו מקבלים 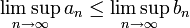
2. הפרכה פשוטה: 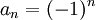
3. הוכחה:
ידוע מתרגילי הבית כי 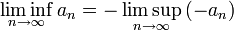
לכן, לפי סעיף א',
תרגיל.
תהי  סדרה חסומה המקיימת
סדרה חסומה המקיימת
הוכח כי קבוצת הגבולות החלקיים של  שווה ל-
שווה ל- ![\Big[\liminf_{n\to\infty}a_n,\limsup a_n\Big]](/images/math/5/6/a/56abb511229aa3d740b072bcde60cc30.png)
- הוכחה
- נסמן את קבוצת הגבולות החלקיים של הסדרה
 ב-A.
ב-A.
- כיון שהגבול החלקי העליון הוא גבול חלקי (לפי משפט) וכך גם לגבי הגבול החלקי התחתון, מתקיים
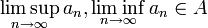
- כיון שהגבול החלקי העליון הוא הגבול החלקי הגדול ביותר, והגבול החלקי התחתון הוא הגבול החלקי הקטן ולכן אם
 אזי בהכרח
אזי בהכרח ![x\in\Big[\liminf a_n,\limsup a_n\Big]](/images/math/c/6/f/c6fdfa11c96ca5fb2468f6f502f939f2.png) .
.
- נניח בשלילה כי קיימת נקודה
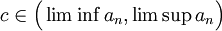 שאינה גבול חלקי של הסדרה
שאינה גבול חלקי של הסדרה
- אזי קיימת סביבת אפסילון של c, המוכלת ממש בקטע, בה יש מספר סופי בלבד של איברים מהסדרה
- נזרוק מספר סופי של איברים מהסדרה כך שבסביבת האפסילון של c לא יהיו איברים כלל. הגבולות החלקיים לא ישתנו כמובן.
- כיוון שהגבול החלקי התחתון הוא בפרט גבול חלקי, יש אינסוף איברים בסדרה הקרובים אליו כרצוננו. בפרט יש אינסוף איברים הקטנים מ
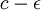 וכמו כן יש אינסוף איברים הגדולים מ
וכמו כן יש אינסוף איברים הגדולים מ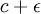
- כיוון שנתון
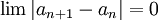 קיים
קיים 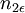 כך שלכל
כך שלכל 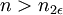 מתקיים
מתקיים 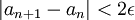
- ניקח שני איברים
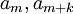 האחד נמצא מימין לסביבת האפסילון של c והשני נמצא משמאל. עוד נקבע כי
האחד נמצא מימין לסביבת האפסילון של c והשני נמצא משמאל. עוד נקבע כי 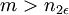 (זה מותר כיוון שיש אינסוף איברים כאלה לפי הטענות הקודמות)
(זה מותר כיוון שיש אינסוף איברים כאלה לפי הטענות הקודמות)
- נוציא מבין
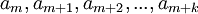 זוג עוקב שהאחד נמצא מימין לסביבת האפסילון של c והשני משמאל
זוג עוקב שהאחד נמצא מימין לסביבת האפסילון של c והשני משמאל
- המרחק בין שני איברי הזוג העוקב הזה גדול מ-
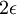 בסתירה.
בסתירה.
תרגיל.
תהיינה 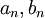 סדרות חסומות. הוכיחו כי:
סדרות חסומות. הוכיחו כי:
הוכחה.
הצד הימני של אי השיוויון:
- קיימת לסדרה
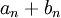 תת סדרה
תת סדרה 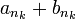 המתכנסת לגבול החלקי העליון
המתכנסת לגבול החלקי העליון 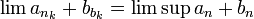
- (שימו לב שתת הסדרה
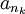 לא בהכרח מתכנסת.)
לא בהכרח מתכנסת.)
- תת הסדרה
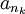 חסומה, ולכן יש לה תת סדרה מתכנסת
חסומה, ולכן יש לה תת סדרה מתכנסת 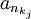 .
.
- כיוון שתת הסדרה
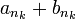 מתכנסת, כל תת סדרה שלה מתכנסת לאותו הגבול. לכן
מתכנסת, כל תת סדרה שלה מתכנסת לאותו הגבול. לכן 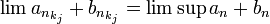
- ביחד, אנו מקבלים כי
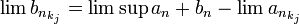 (אריתמטיקה של גבולות של סדרות מתכנסות).
(אריתמטיקה של גבולות של סדרות מתכנסות).
- כלומר, הראנו כי תת הסדרה
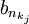 מתכנס.
מתכנס.
- ברור שכל גבול חלקי קטן או שווה לגבול העליון, ולכן
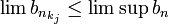 וכמו כן
וכמו כן 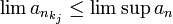
- ביחד מקבלים
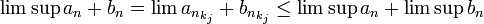 , כפי שרצינו.
, כפי שרצינו.
הצד השמאלי של אי השיוויון:
- קיימת תת סדרה
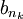 השואפת לגבול העליון של הסדרה
השואפת לגבול העליון של הסדרה  , כלומר
, כלומר 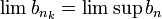
- תת הסדרה המקבילה
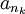 אמנם לא בהכרח מתכנסת, אך כיוון שהיא חסומה, יש לה תת סדרה מתכנסת
אמנם לא בהכרח מתכנסת, אך כיוון שהיא חסומה, יש לה תת סדרה מתכנסת 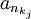
- ברור שכל גבול חלקי גדול או שווה לגבול החלקי התחתון, ולכן
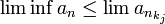
- כמו כן, כיוון שהסדרה
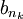 מתכנסת, כל תת סדרה שלה מתכנסת לאותו הגבול. כלומר
מתכנסת, כל תת סדרה שלה מתכנסת לאותו הגבול. כלומר 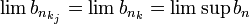
- ביחד מקבלים כי
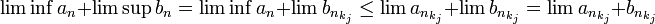
- ברור שכל גבול חלקי קטן או שווה לגבול החלקי העליון, ולכן
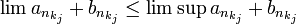 . לכן הוכחנו את הצד השמאלי של אי השיוויון.
. לכן הוכחנו את הצד השמאלי של אי השיוויון.