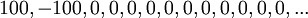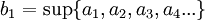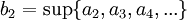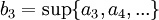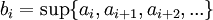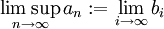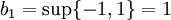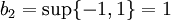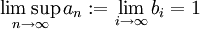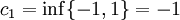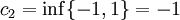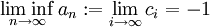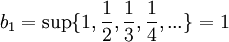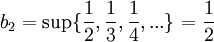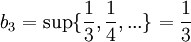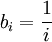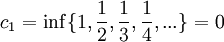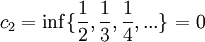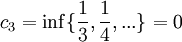88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/גבול עליון ותחתון
גבול עליון וגבול תחתון
למדנו על חסמים על מנת לחסום את הקבוצה באופן אידיאלי, כלומר למצוא את "קצות" הקבוצה. היינו רוצים למצוא הגדרה דומה עבור סדרות. השיטה התמימה היא להביט בחסמים של קבוצת איברי הסדרה, אך מהדוגמא הקלה הבאה נראה כי החסמים של קבוצת איברי הסדרה לא אומרים שום דבר על הסדרה:
החסמים הם פלוס מינוס מאה, אך אין קשר בין מספרים אלה להתנהגות הסדרה באינסוף.
הגדרה.
נגדיר
כלומר, אנו לוקחים את החסם העליון של קבוצת איברי הסדרה, אבל כל פעם אנחנו זורקים את האיבר הבא מהסדרה. באופן טבעי, החסם העליון לא יגדל לאחר שנזרוק איבר.
אם כך, סדרת החסמים 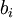 מונוטונית יורדת ולכן שואפת למספר כלשהו או למינוס אינסוף. אם הסדרה חסומה, לפי תרגיל מתקיים
מונוטונית יורדת ולכן שואפת למספר כלשהו או למינוס אינסוף. אם הסדרה חסומה, לפי תרגיל מתקיים 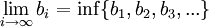
נגדיר
את הגבול העליון של הסדרה  להיות
להיות
במילים בלתי מדוייקות, הגבול העליון הוא החסם העליון "באינסוף".
באופן דומה, הגבול התחתון הינו גבול החסמים התחתונים של קבוצות איברי הסדרה.
העשרה: סדרה הינה פונקציה 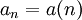 מהטבעיים לקבוצה A, כלומר יחס חד ערכי ושלם
מהטבעיים לקבוצה A, כלומר יחס חד ערכי ושלם 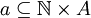 . אם כך, אנו מגדירים
. אם כך, אנו מגדירים
![b_i:=\sup\Big[im \big[a\cap(\mathbb{N}-\{1,2,...,i-1\})\times A\big]\Big]](/images/math/7/2/9/72946e43d170517e8dce687f60498548.png)
דוגמאות.
- נביט בסדרה
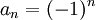 . נבנה את סדרת החסמים
. נבנה את סדרת החסמים 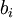 :
:
ולכן הגבול העליון הינו
נביט כעת בסדרת החסמים 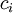 :
:
ולכן הגבול התחתון הינו
- נביט בסדרה
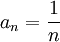 .
.
ולכן הגבול העליון הינו 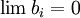
ולכן הגבול התחתון הינו 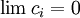
הקשר בין גבול עליון וגבול תחתון להתכנסות סדרות ותתי סדרות
משפט. לכל סדרה יש תת סדרה המתכנסת לגבול העליון שלה, ותת סדרה המתכנסת לגבול התחתון שלה.
לכן הגבול העליון הוא מקסימום מקבוצת הגבולות החלקיים, והגבול התחתון הוא מינימום מקבוצת הגבולות החלקיים.
משפט. גבול סדרה שווה L אם"ם הגבול העליון של הסדרה שווה לגבול התחתון של הסדרה שווה ל- L.