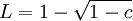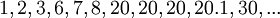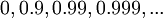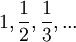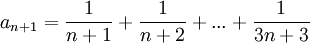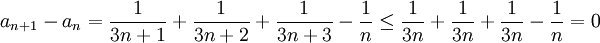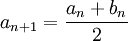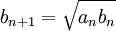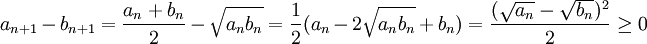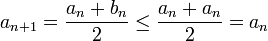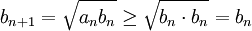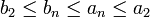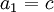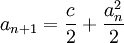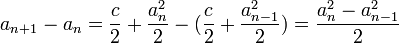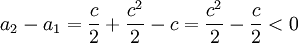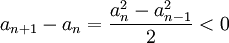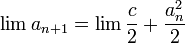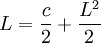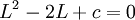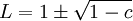88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/מונוטוניות

חזרה לסדרות

סדרות מונוטוניות

הגדרה. סדרה נקראת מונוטונית עולה (יורדת) אם כל איבר בה גדול שווה לקודמו (קטן שווה לקודמו)

דוגמאות.

• $1,2,3,6,7,8,20,20,20,20.1,30,...$

• $0,0.9,0.99,0.999,...$

• $1,\frac{1}{2},\frac{1}{3},...$

משפט. סדרה מונוטונית וגם חסומה מתכנסת. סדרה מונוטונית שאינה חסומה, מתכנסת במובן הרחב.

תרגיל.

הוכח שהסדרה הבאה מתכנסת 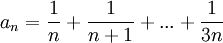$a_n=\frac{1}{n}+\frac{1}{n+1}+...+\frac{1}{3n}$

פתרון. נוכיח כי הסדרה מונוטונית וחסומה, ואז מתכנסת לפי המשפט. נוכיח כי לכל n מתקיים 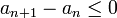$a_{n+1}-a_n\leq 0$ ולכן הסדרה מונוטונית יורדת.

$a_{n+1}=\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{3n+3}$

$a_{n+1}-a_n=\frac{1}{3n+1}+\frac{1}{3n+2}+\frac{1}{3n+3}-\frac{1}{n}\leq \frac{1}{3n}+\frac{1}{3n}+\frac{1}{3n}-\frac{1}{n}=0$

לכן הסדרה מונוטונית יורדת, יש לחסום אותה מלמטה על מנת שתתכנס. אבל קל לראות שכל איברי הסדרה חיוביים ולכן חסומים מלמטה על ידי אפס, ולכן הסדרה מתכנסת.

תרגיל.

יהיו 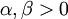$\alpha,\beta>0$ ונגדיר 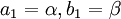$a_1=\alpha,b_1=\beta$. כעת, נגדיר סדרות באמצעות נוסחאת הנסיגה (כלומר כל איבר בסדרה יוגדר באמצעות קודמיו):

$a_{n+1}=\frac{a_n+b_n}{2}$

$b_{n+1}=\sqrt{a_nb_n}$

הוכיח כי שתי הסדרות מתכנסות.

פתרון. אנו נוכיח כי שתי הסדרות מונוטוניות וחסומות. ראשית, נוכיח כי איברי הסדרה $a_n$ גדולים בהתאמה מאיברה הסדרה $b_n$ (פרט אולי לאיבר הראשון שיכול להבחר באופן חופשי). נשים לב כי לפי הגדרת הסדרות והאיברים הראשונים, כל איברי הסדרות הינם אי שליליים.

$a_{n+1}-b_{n+1}=\frac{a_n+b_n}{2}-\sqrt{a_nb_n}=\frac{1}{2}(a_n-2\sqrt{a_nb_n}+b_n)=\frac{(\sqrt{a_n}-\sqrt{b_n})^2}{2}\geq 0$

אם כך, מתקיים כי

$a_{n+1}=\frac{a_n+b_n}{2}\leq\frac{a_n+a_n}{2}=a_n$

ולכן $a_n$ מונוטונית יורדת. כמו כן

$b_{n+1}=\sqrt{a_nb_n}\geq\sqrt{b_n\cdot b_n}=b_n$

ולכן $b_n$ מונוטונית עולה.

נותר להראות כי הסדרות חסומות. נשים לב כי מתקיים:

$b_2\leq b_n\leq a_n \leq a_2$

ולכן שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.

תרגיל.

יהי 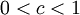$0<c<1$. נגדיר סדרה על ידי תנאי ההתחלה

$a_1=c$

ונוסחאת הנסיגה

$a_{n+1}=\frac{c}{2}+\frac{a_n^2}{2}$

הוכח כי הסדרה מתכנסת ומצא את גבולה.

פתרון.

נבדוק מהו ההפרש בין שני איברים עוקבים על מנת לבדוק מונוטוניות:

$a_{n+1}-a_n=\frac{c}{2}+\frac{a_n^2}{2} - (\frac{c}{2}+\frac{a_{n-1}^2}{2})=\frac{a_n^2-a_{n-1}^2}{2}$

נראה כי הפרש בין זוגות שומר על סימן הזוג הקודם. לכן, נוכיח כי הסדרה מונוטונית באמצעות אינדוקציה:

עבור n=1:

$a_2-a_1=\frac{c}{2}+\frac{c^2}{2}-c=\frac{c^2}{2}-\frac{c}{2}<0$

(זה נכון כיוון ש 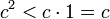$c^2<c\cdot 1 = c$ לפי הנתון $c<1$.)

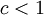נניח, אם כן, כי 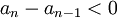$a_n-a_{n-1}<0$ ונוכיח כי 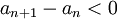$a_{n+1}-a_n<0$. כיוון שכל איברי הסדרה חיוביים (כל איבר בסדרה מוגדר על ידי סכום של קבוע חיובי וריבוע), מותר להעלות את אגפי אי השיוויון בריבוע ולקבל $a_n^2<a_{n-1}^2$.

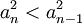לפי החישוב לעיל מתקיים:

$a_{n+1}-a_n=\frac{a_n^2-a_{n-1}^2}{2}<0$

כפי שרצינו.

על כן הסדרה מונוטונית יורדת, וחסומה על ידי אפס (הרי איבריה חיוביים) ולפי המשפט מתכנסת. נותר לנו לחשב את גבולה.

טענה חשובה אך קלה לבדיקה: 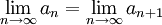$\lim_{n\rightarrow\infty}a_n=\lim_{n\rightarrow\infty}a_{n+1}$. זה נכון כיוון שגבול סדרה נקבע על פי המקום אליה האיברים שואפים באינסוף, ולא על פי מתי היא מתחילה.

שימו לב לשיטה הבאה, היא תשמש אותנו פעמים רבות בתרגילים עם נוסחאות נסיגה. כיוון שהוכחנו שהסדרה מתכנסת (ורק מסיבה זו) ניתן לומר שקיים גבול ממשי L כך ש 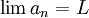$\lim a_n = L$. נביט בנוסחאת הנסיגה

$a_{n+1}=\frac{c}{2}+\frac{a_n^2}{2}$

נפעיל גבול על שני הצדדים (כיוון שזו סדרה מתכנסת, כאמור)

$\lim a_{n+1}=\lim \frac{c}{2}+\frac{a_n^2}{2}$

לפי הטענה לעיל וחשבון גבולות ניתן לומר:

$L=\frac{c}{2}+\frac{L^2}{2}$

$L^2-2L+c=0$

$L=1\pm\sqrt{1-c}$

כעת יש לנו שתי אפשרויות לגבול, נפסול אחת מהן והנותרת בהכרח תהא גבול הסדרה. כיוון ש 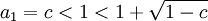$a_1=c<1<1+\sqrt{1-c}$ ושהסדרה מונוטונית יורדת, לא ייתכן כי היא שואפת לגבול זה (קל להראות את קיום שלילת הגבול).

לכן סה"כ, גבול הסדרה הינו $L=1-\sqrt{1-c}$