הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/קושי"
יהודה שמחה (שיחה | תרומות) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 7: | שורה 7: | ||
;<font size=4 color=#3c498e>הגדרה.</font> | ;<font size=4 color=#3c498e>הגדרה.</font> | ||
| − | סדרה <math>a_n</math> נקראת '''סדרת קושי''' אם לכל <math>\varepsilon>0</math> קיים <math>N_\varepsilon\in\N</math> כך שלכל <math>m | + | סדרה <math>a_n</math> נקראת '''סדרת קושי''' אם לכל <math>\varepsilon>0</math> קיים <math>N_\varepsilon\in\N</math> כך שלכל <math>m>n>N_\varepsilon</math> מתקיים <math>|a_m-a_n|<\varepsilon</math> |
במילים, אם לכל מרחק <math>\varepsilon</math> קיים מקום בסדרה כך שהחל ממנו ומעלה המרחק בין '''כל שני אברים''' שואף ל-0, אזי הסדרה הנה סדרת קושי. | במילים, אם לכל מרחק <math>\varepsilon</math> קיים מקום בסדרה כך שהחל ממנו ומעלה המרחק בין '''כל שני אברים''' שואף ל-0, אזי הסדרה הנה סדרת קושי. | ||
| שורה 33: | שורה 33: | ||
| − | <font size=4 color=#a7adcd> | + | ;<font size=4 color=#a7adcd>תרגיל.</font> |
| − | + | תהי סדרה <math>\{a_n\}</math> כך ש- <math>|a_{n+1}-a_n|\le p|a_n-a_{n-1}|</math> עבור <math>0<p<1</math> . הוכח כי <math>\{a_n\}</math> מתכנסת. | |
| − | תהי סדרה <math>\{a_n\}</math> כך ש- <math>|a_{n+1}-a_n|\le p|a_n-a_{n-1}|</math> עבור <math>0<p<1</math> . הוכח | + | |
;פתרון | ;פתרון | ||
| − | נוכיח | + | נוכיח כי <math>\{a_n\}</math> סדרת קושי, ולכן מתכנסת. |
| − | + | ראשית, נשים לב כי <math>|a_{n+1}-a_n|\le p|a_n-a_{n-1}|\le p^2|a_{n-1}-a_{n-2}|\le\cdots\le p^{n-1}|a_2-a_1|</math> . | |
| + | |||
| + | נסמן <math>d=|a_2-a_1|</math> ולכן סה"כ <math>|a_{n+1}-a_n|\le p^{n-1}d</math> | ||
כעת, | כעת, | ||
| − | <math>|a_m-a_n|=|a_m-a_{m-1}+a_{m-1}-a_{m-2}+\cdots-a_{n+1}+a_{n+1}-a_n|\le</math> | + | <math>\begin{align} |
| + | |a_m-a_n|&=\Big|a_m-a_{m-1}+a_{m-1}-a_{m-2}+\cdots+a_{n+2}-a_{n+1}+a_{n+1}-a_n\Big|\\ | ||
| + | &\le|a_m-a_{m-1}|+|a_{m-1}-a_{m-2}|+\cdots+|a_{n+2}-a_{n+1}|+|a_{n+1}-a_n|\\ | ||
| + | &\le p^{m-2}d+\cdots+p^{n-1}d=p^{n-1}d(p^{m-n-1}+\cdots+1)=p^{n-1}d\left(\dfrac{1-p^{m-n-1}}{1-p}\right)\le p^{n-1}\dfrac{d}{1-p}\to0 | ||
| + | \end{align}</math> | ||
| − | + | (לפי מה שהראינו) | |
| − | <math> | + | מכיון ש- <math>p^n\to0</math> עבור <math>p<1</math> . |
| − | |||
| − | |||
| − | |||
| − | |||
| + | ;<font size=4 color=#a7adcd>תרגיל.</font> | ||
תהי <math>a_n</math> סדרה המוגדרת על-ידי כלל הנסיגה | תהי <math>a_n</math> סדרה המוגדרת על-ידי כלל הנסיגה | ||
| שורה 62: | שורה 64: | ||
;הוכחה | ;הוכחה | ||
| − | נוכיח כי זוהי סדרת קושי ולכן מתכנסת. יהי <math>\ | + | נוכיח כי זוהי סדרת קושי ולכן מתכנסת. יהי <math>\varepsilon>0</math> . צריך למצוא מקום בסדרה שהחל ממנו המרחק בין כל שני אברים קטן מ- <math>\varepsilon</math> . נביט במרחק בין שני אברים כלשהם: |
| − | <math>|a_m-a_n|=\Big|a_m-a_{m-1}+a_{m-1}-\cdots+a_{n+1}-a_n\Big|\le</math> | + | <math>\begin{align} |
| + | |a_m-a_n|&=\Big|a_m-a_{m-1}+a_{m-1}-\cdots-a_{n+1}+a_{n+1}-a_n\Big|\\ | ||
| + | &\le|a_m-a_{m-1}|+\cdots+|a_{n+1}-a_n|=\dfrac1{m^2}+\cdots+\dfrac1{(n+1)^2}\\&\le\dfrac1{m(m-1)}+\cdots+\frac1{(n+1)n}\\ | ||
| + | &=\dfrac1{m-1}-\dfrac1m+\dfrac1{m-2}-\dfrac1{m-1}+\cdots+\dfrac1n-\dfrac1{n+1}=\dfrac1n-\dfrac1m\le\dfrac1n\end{align}</math> | ||
| − | + | נעזרנו בנוסחא <math>\dfrac1{k(k-1)}=\dfrac1{k-1}-\dfrac1k</math> | |
| − | <math> | + | וכרגיל, עבור <math>N_\varepsilon>\dfrac1{\varepsilon}</math> אנו מקבלים את מה שצריך לכל <math>m>n>N_\varepsilon</math> |
| − | |||
| − | + | ;<font size=4 color=#a7adcd>תרגיל.</font> | |
| − | + | תהי <math>a_n</math> סדרה המוגדרת על-ידי כלל הנסיגה | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <font size=4 color=#a7adcd> | + | |
| − | + | ||
| − | תהי <math>a_n</math> סדרה המוגדרת על ידי כלל הנסיגה | + | |
| − | + | <math>a_{n+1}=a_n+\dfrac1{n+1}</math> | |
הוכח כי <math>\lim\limits_{n\to\infty}a_n=\infty</math> (כלומר הסדרה מתכנסת במובן הרחב לאינסוף). | הוכח כי <math>\lim\limits_{n\to\infty}a_n=\infty</math> (כלומר הסדרה מתכנסת במובן הרחב לאינסוף). | ||
| − | |||
;הוכחה | ;הוכחה | ||
| − | דבר ראשון, טריוויאלי להוכיח כי הסדרה הנה מונוטונית עולה שכן <math>a_{n+1}-a_n=\ | + | דבר ראשון, טריוויאלי להוכיח כי הסדרה הנה מונוטונית עולה שכן <math>a_{n+1}-a_n=\dfrac1{n+1}>0</math> . |
לכן, כפי שלמדנו, מספיק להוכיח כי הסדרה אינה מתכנסת. לצורך זה, מספיק להוכיח שהיא אינה סדרת קושי. | לכן, כפי שלמדנו, מספיק להוכיח כי הסדרה אינה מתכנסת. לצורך זה, מספיק להוכיח שהיא אינה סדרת קושי. | ||
| − | ניקח <math>\ | + | ניקח <math>\varepsilon=\tfrac12</math>. יהי <math>N\in\N</math> מקום כלשהו בסדרה, ויהי <math>n>N</math> . ניקח <math>m=2n</math> . מתקיים: |
| − | + | ||
| − | + | ||
| − | <math>=\ | + | <math>\begin{align}|a_{2n}-a_n|&=\Big|a_{2n}-a_{2n-1}+a_{2n-1}-\cdots-a_{n+1}+a_{n+1}-a_n\Big|\\ |
| + | &=\frac1{2n}+\cdots+\frac1{n+1}\ge\frac1{2n}+\cdots+\frac1{2n}=\frac{n}{2n}=\frac12\end{align}</math> | ||
ולכן מתקיימת '''שלילת''' ההגדרה של קושי והסדרה הנ"ל אינה מתכנסת. | ולכן מתקיימת '''שלילת''' ההגדרה של קושי והסדרה הנ"ל אינה מתכנסת. | ||
גרסה אחרונה מ־01:27, 16 בפברואר 2017
סדרות קושי
הגדרת התכנסות סדרה עד כה הסתמכה על קיום נקודת גבול  . אולם למדנו כי יש סדרות המתקרבות לנקודה שאינה שייכת לשדה, כמו
. אולם למדנו כי יש סדרות המתקרבות לנקודה שאינה שייכת לשדה, כמו 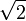 בשדה הרציונאלים. סדרה המתכנסות לשורש שתיים מעל הממשיים, בהכרח אינה מתכנסת מעל הרציונאלים.
בשדה הרציונאלים. סדרה המתכנסות לשורש שתיים מעל הממשיים, בהכרח אינה מתכנסת מעל הרציונאלים.
נגדיר אפוא תכונה של סדרה השקולה מבחינת התנהגות להתכנסות, אך אינה דורשת קיום של נקודת גבול בשדה. עקרונית, נדרוש שאברי הסדרה יתקרבו זה לזה, ולא לנקודת עוגן מסוימת הלא היא נקודת הגבול.
- הגדרה.
סדרה  נקראת סדרת קושי אם לכל
נקראת סדרת קושי אם לכל  קיים
קיים 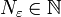 כך שלכל
כך שלכל 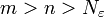 מתקיים
מתקיים 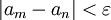
במילים, אם לכל מרחק  קיים מקום בסדרה כך שהחל ממנו ומעלה המרחק בין כל שני אברים שואף ל-0, אזי הסדרה הנה סדרת קושי.
קיים מקום בסדרה כך שהחל ממנו ומעלה המרחק בין כל שני אברים שואף ל-0, אזי הסדרה הנה סדרת קושי.
- משפט.
מעל שדה הממשיים סדרה מתכנסת אם"ם היא סדרת קושי.
ברור ממשפט זה, יחד עם הדוגמא של סדרה השואפת ל- 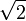 , שהמשפט אינו תקף מעל שדה הרציונאליים.
, שהמשפט אינו תקף מעל שדה הרציונאליים.
- תרגיל.
תהי סדרה 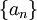 כך ש-
כך ש- 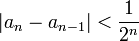 . הוכח כי
. הוכח כי 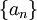 מתכנסת.
מתכנסת.
- פתרון
נוכיח כי 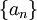 סדרת קושי, ולכן מתכנסת.
סדרת קושי, ולכן מתכנסת.
לפי הנתון
- תרגיל.
תהי סדרה 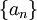 כך ש-
כך ש- 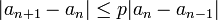 עבור
עבור 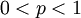 . הוכח כי
. הוכח כי 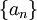 מתכנסת.
מתכנסת.
- פתרון
נוכיח כי 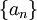 סדרת קושי, ולכן מתכנסת.
סדרת קושי, ולכן מתכנסת.
ראשית, נשים לב כי 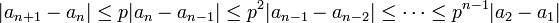 .
.
נסמן 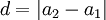 ולכן סה"כ
ולכן סה"כ 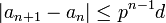
כעת,
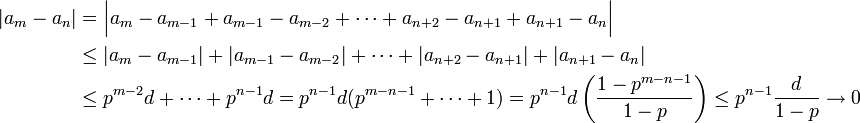
(לפי מה שהראינו)
מכיון ש- 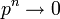 עבור
עבור 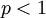 .
.
- תרגיל.
תהי  סדרה המוגדרת על-ידי כלל הנסיגה
סדרה המוגדרת על-ידי כלל הנסיגה
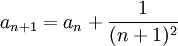
הוכח כי הסדרה מתכנסת.
- הוכחה
נוכיח כי זוהי סדרת קושי ולכן מתכנסת. יהי  . צריך למצוא מקום בסדרה שהחל ממנו המרחק בין כל שני אברים קטן מ-
. צריך למצוא מקום בסדרה שהחל ממנו המרחק בין כל שני אברים קטן מ-  . נביט במרחק בין שני אברים כלשהם:
. נביט במרחק בין שני אברים כלשהם:
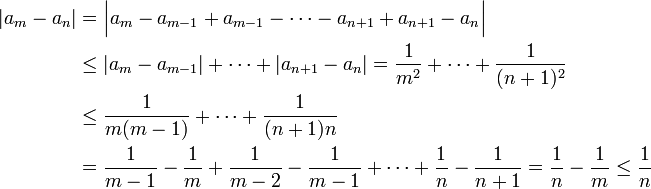
נעזרנו בנוסחא 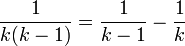
וכרגיל, עבור 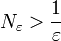 אנו מקבלים את מה שצריך לכל
אנו מקבלים את מה שצריך לכל 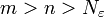
- תרגיל.
תהי  סדרה המוגדרת על-ידי כלל הנסיגה
סדרה המוגדרת על-ידי כלל הנסיגה
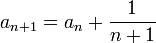
הוכח כי 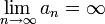 (כלומר הסדרה מתכנסת במובן הרחב לאינסוף).
(כלומר הסדרה מתכנסת במובן הרחב לאינסוף).
- הוכחה
דבר ראשון, טריוויאלי להוכיח כי הסדרה הנה מונוטונית עולה שכן 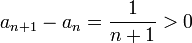 .
.
לכן, כפי שלמדנו, מספיק להוכיח כי הסדרה אינה מתכנסת. לצורך זה, מספיק להוכיח שהיא אינה סדרת קושי.
ניקח 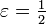 . יהי
. יהי 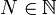 מקום כלשהו בסדרה, ויהי
מקום כלשהו בסדרה, ויהי 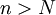 . ניקח
. ניקח 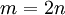 . מתקיים:
. מתקיים:
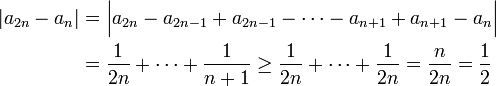
ולכן מתקיימת שלילת ההגדרה של קושי והסדרה הנ"ל אינה מתכנסת.
![\begin{align}
|a_m-a_n|&=\Big|a_m-a_{m-1}+a_{m-1}-a_{m-2}+\cdots+a_{n+2}-a_{n+1}+a_{n+1}-a_n\Big|\\
&\le|a_m-a_{m-1}|+|a_{m-1}-a_{m-2}|+\cdots+|a_{n+2}-a_{n+1}|+|a_{n+1}-a_n|\\
&<\dfrac1{2^m}+\dfrac1{2^{m-1}}+\cdots+\dfrac1{2^{n+1}}=\dfrac1{2^{n+1}}\left[\frac1{2^{m-n-1}}+\cdots+1\right]\\
&=\dfrac1{2^{n+1}}\left[\dfrac{1-\frac1{2^{m-n}}}{1-\frac12}\right]=\frac1{2^n}\left[1-\frac1{2^{m-n}}\right]=\frac1{2^n}-\dfrac1{2^m}\le\dfrac1{2^n}\to0
\end{align}](/images/math/f/3/9/f394606338468c59206fb03b7b28070e.png)