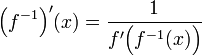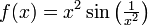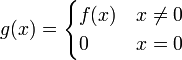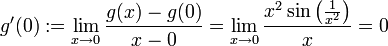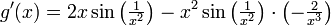הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/פונקציות/גזירות"
(←אריתמטיקה של נגזרות) |
יהודה שמחה (שיחה | תרומות) |
||
| (2 גרסאות ביניים של משתמש אחר אחד אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
==הגדרת הנגזרת== | ==הגדרת הנגזרת== | ||
| + | נגזרת, באופן אינטואיטיבי, מודדת את השיפוע של הפונקציה בנקודה. בדומה למושגים קודמים כמו גבול וסכום טור, אנו נותנים הגדרה מדויקת ל'שיפוע' התואמת את ההגיון ובודקים אילו מן הפונקציות מקיימות הגדרה זו. | ||
| − | + | שיפוע של קו ישר מוגדר על-ידי המרחק בציר <math>y</math> חלקי המרחק בציר <math>x</math> . נביט בקו <math>y(x)=mx+b</math> , אזי השיפוע שלו הוא: | |
| + | :<math>\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{mx_1+b-(mx_2+b)}{x_1-x_2}=m</math> | ||
| − | שיפוע של | + | אם כך, נגדיר שיפוע של פונקציה כללית, לפי '''גבול''' שיפועים של קוים ישרים. לכל נקודה בסביבת <math>x_0</math> נמדוד את השיפוע של הקו הישר בין שתי תמונות הפונקציה מעל הנקודה שבחרנו ומעל <math>x_0</math> . הנגזרת, או השיפוע, ב- <math>x_0</math> מוגדרת להיות גבול השיפועים לעיל כאשר הנקודות מתקרבות ל- <math>x_0</math> . |
| − | + | <font size=4 color=#3c498e>'''הגדרה.'''</font> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <font size=4 color=#3c498e> | + | |
| − | '''הגדרה.''' | + | |
| − | </font | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | תהי <math>f</math> פונקציה המוגדרת בסביבה של נקודה <math>x_0</math> . אזי הפונקציה '''גזירה''' בנקודה <math>x_0</math> אם הגבול הבא קיים וסופי: | ||
| + | :<math>f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}</math> | ||
שימו לב, קל להוכיח שהגדרת הנגזרת שקולה ושווה לגבול הבא: | שימו לב, קל להוכיח שהגדרת הנגזרת שקולה ושווה לגבול הבא: | ||
| + | :<math>f'(x_0)=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}</math> | ||
| + | '''הערה חשובה:''' התייחסו אל <math>\Delta x</math> כאל משתנה יחיד, ולא כפונקציה את <math>x</math> . | ||
| − | + | <font size=4 color=#a7adcd>'''דוגמא.'''</font> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <font size=4 color=#a7adcd> | + | |
| − | '''דוגמא.''' | + | |
| − | </font | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | נגזור את הפונקציה <math>f(x)=\sqrt{x}</math> בנקודה כללית <math>x>0</math> . | ||
| + | :<math>f'(x)=\lim_{\Delta x\to 0}\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}=\lim_{\Delta x\to 0}\frac{x+\Delta x-x}{\Delta x(\sqrt{x+\Delta x}+\sqrt{x})}=\lim_{\Delta x\to 0}\frac{1}{(\sqrt{x+\Delta x}+\sqrt{x})}=\frac{1}{2\sqrt{x}}</math> | ||
==אריתמטיקה של נגזרות ושאר נוסחאות== | ==אריתמטיקה של נגזרות ושאר נוסחאות== | ||
| + | :<math>(c\cdot f)'=c\cdot f'</math> | ||
| − | + | :<math>(f+g)'=f'+g'</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
שימו לב: משני תנאים אלה ניתן לראות כי 'נגזרת' היא אופרטור לינארי על מרחב הפונקציות (שהוא אכן מרחב וקטורי). | שימו לב: משני תנאים אלה ניתן לראות כי 'נגזרת' היא אופרטור לינארי על מרחב הפונקציות (שהוא אכן מרחב וקטורי). | ||
| + | :<math>(f\cdot g)'=f'g+g'f</math> | ||
| + | :<math>\left(\frac{f}{g}\right)'=\frac{f'g-g'f}{g^2}</math> | ||
| − | + | :<math>\Big(f(g)\Big)'=f'(g)\cdot g'</math> | |
| + | :<math>(f^g)'=f^g\Big[g'\ln(f)+\frac{gf'}{f}\Big]</math> | ||
| − | : | + | שימו לב: זו בעצם נגזרת ההרכבה <math>f^g=e^{\ln(f^g)}=e^{g\ln(f)}</math> |
| + | :<math>\Big(f^{-1}\Big)'(x)=\frac{1}{f'\Big(f^{-1}(x)\Big)}</math> | ||
| − | + | ==נגזרות של פונקציות נפוצות== | |
| − | + | *[[מדיה:09Infi2Derivatives.jpg|דף נוסחאות של נגזרות]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | : | + | |
==רציפות הנגזרת== | ==רציפות הנגזרת== | ||
| שורה 74: | שורה 48: | ||
נחקור לצורך מענה על השאלה את הפונקציה הבאה: | נחקור לצורך מענה על השאלה את הפונקציה הבאה: | ||
| + | :<math>f(x)=x^2\sin\left(\tfrac{1}{x^2}\right)</math> | ||
| + | כיון שזו הרכבה וחלוקה של פונקציות גזירות, זו פונקציה רציפה וגזירה לכל <math>x\ne 0</math>. בנקודה אפס הפונקציה אינה מוגדרת ולכן אינה רציפה ואינה גזירה. | ||
| − | ::<math> | + | אולם, נוכיח כי אי-הרציפות ב- <math>0</math> הנה סליקה, ונתקן את הפונקציה לקבל פונקציה רציפה על כל הממשיים: |
| + | :<math>g(x)=\begin{cases}f(x) & x\ne 0\\0 & x=0\end{cases}</math> | ||
| + | (קל לבדוק כי <math>\lim_{x\to 0}g(x)=0</math> ולכן הפונקציה רציפה על כל הממשיים). | ||
| + | האם <math>g</math> גזירה ב- <math>0</math> ? יש לבדוק ישירות מתוך ההגדרה (כיון שהיא לא מוגדרת על-ידי פונקציות אלמנטריות בנקודה זו). | ||
| + | :<math>g'(0):=\lim_{x\to 0}\frac{g(x)-g(0)}{x-0}=\lim_{x\to 0}\frac{x^2\sin\left(\tfrac{1}{x^2}\right)}{x}=0</math> | ||
| + | על כן <math>g</math> גזירה ב- <math>0</math> , וביחד היא גזירה על כל הממשיים. | ||
| + | :<math>g'(x)=2x\sin\left(\tfrac{1}{x^2}\right)-x^2\sin\left(\tfrac{1}{x^2}\right)\cdot\left(-\tfrac{2}{x^3}\right)</math> | ||
| − | + | וקל לראות שפונקציה זו אינה חסומה באף סביבה של <math>0</math> ולכן אינה רציפה שם. | |
| − | + | ==מונוטוניות== | |
| + | '''משפט.''' אם הנגזרת של <math>f</math> אי שלילית בקטע מסוים, אזי <math>f</math> מונוטונית לא יורדת בו. באופן דומה, אם הנגזרת אי חיובית, אזי הפונקציה מונוטונית לא עולה. | ||
| − | + | ==פרמה, רול ולגראנז'== | |
| + | [[משפט פרמה (אינפי)|משפט פרמה]] | ||
| − | + | [[משפט רול]] | |
| − | + | [[משפט לגראנז' (אינפי)|משפט לגראנז']] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
גרסה אחרונה מ־11:38, 7 ביוני 2016
תוכן עניינים
הגדרת הנגזרת
נגזרת, באופן אינטואיטיבי, מודדת את השיפוע של הפונקציה בנקודה. בדומה למושגים קודמים כמו גבול וסכום טור, אנו נותנים הגדרה מדויקת ל'שיפוע' התואמת את ההגיון ובודקים אילו מן הפונקציות מקיימות הגדרה זו.
שיפוע של קו ישר מוגדר על-ידי המרחק בציר  חלקי המרחק בציר
חלקי המרחק בציר  . נביט בקו
. נביט בקו 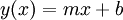 , אזי השיפוע שלו הוא:
, אזי השיפוע שלו הוא:
אם כך, נגדיר שיפוע של פונקציה כללית, לפי גבול שיפועים של קוים ישרים. לכל נקודה בסביבת  נמדוד את השיפוע של הקו הישר בין שתי תמונות הפונקציה מעל הנקודה שבחרנו ומעל
נמדוד את השיפוע של הקו הישר בין שתי תמונות הפונקציה מעל הנקודה שבחרנו ומעל  . הנגזרת, או השיפוע, ב-
. הנגזרת, או השיפוע, ב-  מוגדרת להיות גבול השיפועים לעיל כאשר הנקודות מתקרבות ל-
מוגדרת להיות גבול השיפועים לעיל כאשר הנקודות מתקרבות ל-  .
.
הגדרה.
תהי  פונקציה המוגדרת בסביבה של נקודה
פונקציה המוגדרת בסביבה של נקודה  . אזי הפונקציה גזירה בנקודה
. אזי הפונקציה גזירה בנקודה  אם הגבול הבא קיים וסופי:
אם הגבול הבא קיים וסופי:
שימו לב, קל להוכיח שהגדרת הנגזרת שקולה ושווה לגבול הבא:
הערה חשובה: התייחסו אל 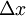 כאל משתנה יחיד, ולא כפונקציה את
כאל משתנה יחיד, ולא כפונקציה את  .
.
דוגמא.
נגזור את הפונקציה 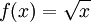 בנקודה כללית
בנקודה כללית 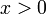 .
.
אריתמטיקה של נגזרות ושאר נוסחאות
שימו לב: משני תנאים אלה ניתן לראות כי 'נגזרת' היא אופרטור לינארי על מרחב הפונקציות (שהוא אכן מרחב וקטורי).
שימו לב: זו בעצם נגזרת ההרכבה 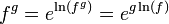
נגזרות של פונקציות נפוצות
רציפות הנגזרת
שאלה, האם קיימת פונקציה הגזירה בקטע פתוח שנגזרתה אינה רציפה בקטע זה?
נחקור לצורך מענה על השאלה את הפונקציה הבאה:
כיון שזו הרכבה וחלוקה של פונקציות גזירות, זו פונקציה רציפה וגזירה לכל 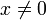 . בנקודה אפס הפונקציה אינה מוגדרת ולכן אינה רציפה ואינה גזירה.
. בנקודה אפס הפונקציה אינה מוגדרת ולכן אינה רציפה ואינה גזירה.
אולם, נוכיח כי אי-הרציפות ב-  הנה סליקה, ונתקן את הפונקציה לקבל פונקציה רציפה על כל הממשיים:
הנה סליקה, ונתקן את הפונקציה לקבל פונקציה רציפה על כל הממשיים:
(קל לבדוק כי 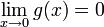 ולכן הפונקציה רציפה על כל הממשיים).
ולכן הפונקציה רציפה על כל הממשיים).
האם  גזירה ב-
גזירה ב-  ? יש לבדוק ישירות מתוך ההגדרה (כיון שהיא לא מוגדרת על-ידי פונקציות אלמנטריות בנקודה זו).
? יש לבדוק ישירות מתוך ההגדרה (כיון שהיא לא מוגדרת על-ידי פונקציות אלמנטריות בנקודה זו).
על כן  גזירה ב-
גזירה ב-  , וביחד היא גזירה על כל הממשיים.
, וביחד היא גזירה על כל הממשיים.
וקל לראות שפונקציה זו אינה חסומה באף סביבה של  ולכן אינה רציפה שם.
ולכן אינה רציפה שם.
מונוטוניות
משפט. אם הנגזרת של  אי שלילית בקטע מסוים, אזי
אי שלילית בקטע מסוים, אזי  מונוטונית לא יורדת בו. באופן דומה, אם הנגזרת אי חיובית, אזי הפונקציה מונוטונית לא עולה.
מונוטונית לא יורדת בו. באופן דומה, אם הנגזרת אי חיובית, אזי הפונקציה מונוטונית לא עולה.
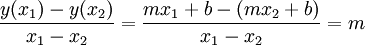
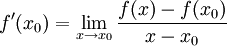
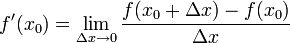
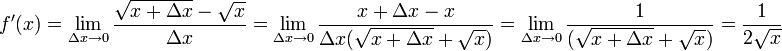
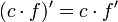
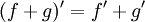
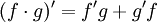
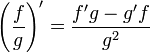
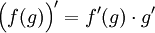
![(f^g)'=f^g\Big[g'\ln(f)+\frac{gf'}{f}\Big]](/images/math/8/5/a/85a6319ba0c497d2ae863233407a8d76.png)