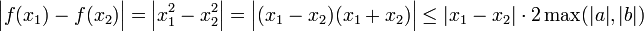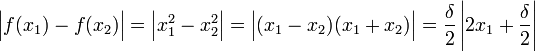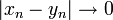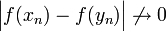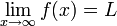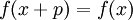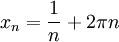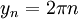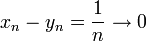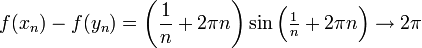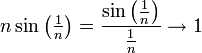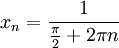הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/פונקציות/רציפות במ"ש"
(←משפט - סכום רציפות במ"ש) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 4: | שורה 4: | ||
עד כה הגדרנו רציפות באופן נקודתי ואמרנו שפונקציה רציפה בקטע אם היא רציפה בכל נקודה בקטע בנפרד. | עד כה הגדרנו רציפות באופן נקודתי ואמרנו שפונקציה רציפה בקטע אם היא רציפה בכל נקודה בקטע בנפרד. | ||
| − | באופן אינטואיטיבי, אומרים כי פונקציה מתכנסת 'יותר מהר' אל הגבול שלה, אם הדלתא הנדרש לאפסילון הוא גדול יותר (כלומר הפונקציה קרובה לגבול בתחום יותר רחב). אנו רוצים להגדיר פונקציות אשר מהירות ההתכנסות שלהן דומה בכל נקודה בקטע | + | באופן אינטואיטיבי, אומרים כי פונקציה מתכנסת 'יותר מהר' אל הגבול שלה, אם הדלתא הנדרש לאפסילון הוא גדול יותר (כלומר הפונקציה קרובה לגבול בתחום יותר רחב). אנו רוצים להגדיר פונקציות אשר מהירות ההתכנסות שלהן דומה בכל נקודה בקטע מסוים. |
| שורה 10: | שורה 10: | ||
'''הגדרה.''' | '''הגדרה.''' | ||
</font> | </font> | ||
| − | פונקציה f נקראת '''רציפה במידה שווה''' (רציפה במ"ש) בקטע A אם: | + | פונקציה <math>f</math> נקראת '''רציפה במידה שווה''' (רציפה במ"ש) בקטע A אם: |
| − | *לכל <math>\epsilon >0</math> קיים <math>\delta>0</math> כך שלכל זוג נקודות <math>x_1,x_2\in A</math> המקיימות <math>|x_1-x_2|<\delta</math> מתקיים <math>|f(x_1)-f(x_2)|<\epsilon</math> | + | *לכל <math>\epsilon>0</math> קיים <math>\delta>0</math> כך שלכל זוג נקודות <math>x_1,x_2\in A</math> המקיימות <math>|x_1-x_2|<\delta</math> מתקיים <math>\Big|f(x_1)-f(x_2)\Big|<\epsilon</math> . |
| − | שימו לב כי ברציפות רגילה בקטע A, לכל נקודה בקטע ההתאמה של הדלתא לאפסילון | + | שימו לב כי ברציפות רגילה בקטע A, לכל נקודה בקטע ההתאמה של הדלתא לאפסילון עשויה להיות שונה. כאשר הפונקציה רציפה במ"ש, לכל אפסילון יש דלתא המתאים לכל הקטע A. |
'''הערה:''' ברור שאם פונקציה רציפה במ"ש על קטע A, היא גם רציפה במ"ש על כל קטע המוכל ב-A. | '''הערה:''' ברור שאם פונקציה רציפה במ"ש על קטע A, היא גם רציפה במ"ש על כל קטע המוכל ב-A. | ||
| שורה 22: | שורה 22: | ||
</font> | </font> | ||
| − | נבחן את הפונקציה <math>f(x)=x</math>, ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים. | + | נבחן את הפונקציה <math>f(x)=x</math> , ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים. |
| − | אכן, לכל אפסילון ניקח דלתא שווה לאפסילון ונקבל כי <math>|f(x_1)-f(x_2)|=|x_1-x_2|<\delta=\epsilon</math> | + | אכן, לכל אפסילון ניקח דלתא שווה לאפסילון ונקבל כי <math>\Big|f(x_1)-f(x_2)\Big|=|x_1-x_2|<\delta=\epsilon</math> |
| + | בדוגמא הבאה נלמד כי פונקציה מסוימת עשוייה להיות רציפה במ"ש בקטע מסוים אך לא רציפה במ"ש בקטע אחר. כפי שנראה בהמשך, כל פונקציה הרציפה על קטע סופי וסגור רציפה בו במ"ש, ואילו ישנן פונקציות רציפות שאינן רציפות במ"ש על כל ציר הממשיים. | ||
| − | |||
| + | ראשית, נביט ב <math>f(x)=x^2</math> על הקטע הסופי <math>(a,b)</math> . יהי <math>\epsilon>0</math> , אזי: | ||
| + | :<math>\Big|f(x_1)-f(x_2)\Big|=\Big|x_1^2-x_2^2\Big|=\Big|(x_1-x_2)(x_1+x_2)\Big|\le|x_1-x_2|\cdot2\max(|a|,|b|)</math> | ||
| − | + | כעת, אם ניקח <math>\delta=\frac{\epsilon}{2\max(|a|,|b|)}</math> נקבל את הדרוש. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | כעת, אם ניקח <math>\delta = \frac{\epsilon}{ | + | |
| שורה 41: | שורה 39: | ||
עכשיו, נבחן את אותה הפונקציה <math>f(x)=x^2</math> על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש. | עכשיו, נבחן את אותה הפונקציה <math>f(x)=x^2</math> על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש. | ||
| − | ניקח <math>\epsilon=1</math>. צריך להוכיח כי לכל <math>\delta>0</math> קיים זוג מספרים ממשיים המקיימים <math>|x_1-x_2|<\delta</math> וגם <math>|f(x_1)-f(x_2)|\ | + | ניקח <math>\epsilon=1</math> . צריך להוכיח כי לכל <math>\delta>0</math> קיים זוג מספרים ממשיים המקיימים <math>|x_1-x_2|<\delta</math> וגם <math>\Big|f(x_1)-f(x_2)\Big|\ge1</math> . |
| − | + | ||
ניקח <math>x_2=x_1+\frac{\delta}{2}</math> ונראה כי אם נבחר את <math>x_1</math> להיות גדול מספיק, נקבל את הדרוש. ברור כי <math>|x_1-x_2|=\frac{\delta}{2}<\delta</math> | ניקח <math>x_2=x_1+\frac{\delta}{2}</math> ונראה כי אם נבחר את <math>x_1</math> להיות גדול מספיק, נקבל את הדרוש. ברור כי <math>|x_1-x_2|=\frac{\delta}{2}<\delta</math> | ||
| − | + | :<math>\Big|f(x_1)-f(x_2)\Big|=\Big|x_1^2-x_2^2\Big|=\Big|(x_1-x_2)(x_1+x_2)\Big|=\frac{\delta}{2}\left|2x_1+\frac{\delta}{2}\right|</math> | |
| − | + | ||
ברור שאם נגדיל את <math>x_1</math> מספיק נקבל את הדרוש. | ברור שאם נגדיל את <math>x_1</math> מספיק נקבל את הדרוש. | ||
| − | |||
==מבחנים לבדיקה האם פונקציה רציפה במ"ש== | ==מבחנים לבדיקה האם פונקציה רציפה במ"ש== | ||
| שורה 60: | שורה 55: | ||
סכום וכפל בקבוע של רציפות במ"ש - רציף במ"ש. | סכום וכפל בקבוע של רציפות במ"ש - רציף במ"ש. | ||
| − | שימו לב, כפל אינו רציף במ"ש בהכרח, לדוגמא <math>x^2=x\cdot x</math>, כאשר הפונקציה משמאל אינה רציפה במ"ש על כל הממשיים, ואילו הפונקציות מימין כן. | + | שימו לב, כפל אינו רציף במ"ש בהכרח, לדוגמא <math>x^2=x\cdot x</math> , כאשר הפונקציה משמאל אינה רציפה במ"ש על כל הממשיים, ואילו הפונקציות מימין כן. |
===משפט - תנאי שקול לאי-רציפות במ"ש - שיטת הסדרות=== | ===משפט - תנאי שקול לאי-רציפות במ"ש - שיטת הסדרות=== | ||
| − | פונקציה f '''אינה''' רציפה במ"ש בקטע A אם"ם קיים זוג סדרות (עם | + | פונקציה f '''אינה''' רציפה במ"ש בקטע A אם"ם קיים זוג סדרות (עם אברים מ-A) המקיימות: |
| − | + | :<math>|x_n-y_n|\rightarrow0</math> | |
| − | + | ||
| − | + | ||
וגם | וגם | ||
| − | + | :<math>\Big|f(x_n)-f(y_n)\Big|\not\rightarrow0</math> | |
| − | + | ||
| − | + | ||
'''הוכחה.''' | '''הוכחה.''' | ||
| − | אם הפונקציה אינה רציפה במ"ש אזי קיים | + | אם הפונקציה אינה רציפה במ"ש אזי קיים <math>\epsilon>0</math> כך שלכל <math>\delta>0</math> יש זוג מספרים בקטע במרחק קטן מדלתא, כך שהפרש התמונות ביניהם גדול או שווה לאפסילון. |
ניקח סדרת דלתאות כלשהי השואפת לאפס. הסדרות המורכבות מהזוגות המותאמים לדלתאות מקיימות את הדרוש. | ניקח סדרת דלתאות כלשהי השואפת לאפס. הסדרות המורכבות מהזוגות המותאמים לדלתאות מקיימות את הדרוש. | ||
| − | + | בכיוון ההפוך, אם יש זוג סדרות כזה, כיון שסדרת ההפרשים בין התמונות אינה שואפת לאפס יש לה תת-סדרה שמתכנסת למספר שונה מאפס (הגבול העליון). תת הסדרות המתאימות של הזוגות יספקו זוג מתאים לכל דלתא, כאשר האפסילון יהיה חצי מגבול סדרת ההפרשים. | |
| − | בכיוון ההפוך, אם יש זוג סדרות כזה, | + | |
===משפט - תנאי הכרחי (אבל לא מספיק) לרציפות במ"ש - חסימות על קטע סופי=== | ===משפט - תנאי הכרחי (אבל לא מספיק) לרציפות במ"ש - חסימות על קטע סופי=== | ||
פונקציה רציפה במ"ש על קטע סופי חסומה שם | פונקציה רציפה במ"ש על קטע סופי חסומה שם | ||
| − | דוגמא נגדית לכיוון ההפוך - <math>f(x)=sin\ | + | דוגמא נגדית לכיוון ההפוך - <math>f(x)=\sin\left(\tfrac{1}{x}\right)</math> חסומה אך אינה רציפה במ"ש בקטע <math>(0,1)</math> |
===משפט קנטור=== | ===משפט קנטור=== | ||
| שורה 91: | שורה 81: | ||
===משפט - הרכבת פונקציות רציפות במ"ש=== | ===משפט - הרכבת פונקציות רציפות במ"ש=== | ||
| − | נניח f רציפה במ"ש על קטע המכיל את התמונה של פונקציה רציפה במ"ש g. אזי ההרכבה <math>f(g(x))</math> רציפה במ"ש | + | נניח <math>f</math> רציפה במ"ש על קטע המכיל את התמונה של פונקציה רציפה במ"ש <math>g</math> . אזי ההרכבה <math>f(g(x))</math> רציפה במ"ש |
| − | ===משפט - חלוקה לתתי קטעים=== | + | ===משפט - חלוקה לתתי-קטעים=== |
אם <math>f</math> רציפה במ"ש על הקטעים <math>(a,b],[b,c)</math> (לאו דווקא קצות סופיים), אזי היא רציפה במ"ש באיחוד <math>(a,c)</math> | אם <math>f</math> רציפה במ"ש על הקטעים <math>(a,b],[b,c)</math> (לאו דווקא קצות סופיים), אזי היא רציפה במ"ש באיחוד <math>(a,c)</math> | ||
'''הוכחה.''' | '''הוכחה.''' | ||
| − | יהי <math>\epsilon>0</math>. | + | יהי <math>\epsilon>0</math> . |
| − | <math>f</math> רציפה במ"ש ב | + | <math>f</math> רציפה במ"ש ב- <math>(a,b]</math> ולכן קיים <math>\delta_1>0</math> כך שלכל <math>x,y\in(a,b]</math> המקיימים <math>|x-y|<\delta_1</math> מתקיים <math>\Big|f(x)-f(y)\Big|<\frac{\epsilon}{2}</math> . |
| − | <math>f</math> רציפה במ"ש ב | + | <math>f</math> רציפה במ"ש ב- <math>[b,c)</math> ולכן קיים <math>\delta_2>0</math> כך שלכל <math>x,y\in[b,c)</math> המקיימים <math>|x-y|<\delta_2</math> מתקיים <math>\Big|f(x)-f(y)\Big|<\frac{\epsilon}{2}</math> . |
| − | יהי <math>\delta=\min\{\delta_1,\delta_2\}</math>. אזי <math>\delta>0</math>. נראה שלכל <math>x,y\in(a,c)</math> המקיימים <math>|x-y|<\delta</math> מתקיים <math>|f(x)-f(y)|<\epsilon</math>. | + | יהי <math>\delta=\min\{\delta_1,\delta_2\}</math> . אזי <math>\delta>0</math>. נראה שלכל <math>x,y\in(a,c)</math> המקיימים <math>|x-y|<\delta</math> מתקיים <math>\Big|f(x)-f(y)\Big|<\epsilon</math> . |
| − | + | ||
| − | + | נניח <math>x,y\in(a,c)</math> כך ש- <math>|x-y|<\delta</math> . יתכנו שלושה מצבים: | |
| − | + | ||
| − | + | א) <math>x,y\in(a,b]</math> . אזי <math>|x-y|<\delta\le\delta_1</math> ומכאן <math>\Big|f(x)-f(y)\Big|<\frac{\epsilon}{2}<\epsilon</math> . | |
| − | ג) אחת מהנקודות ב <math>(a,b]</math> והשניה ב <math>[b,c)</math>. נניח בה"כ ש <math>x\in | + | ב) <math>x,y\in[b,c)</math> ומכיון ש- <math>|x-y|<\delta\le\delta_2</math> נסיק ש- <math>\Big|f(x)-f(y)\Big|<\frac{\epsilon}{2}<\epsilon</math> . |
| − | (a,b]</math> ו | + | |
| − | וכן <math>|y-b|\ | + | ג) אחת מהנקודות ב- <math>(a,b]</math> והשניה ב- <math>[b,c)</math> . נניח בה"כ ש- <math>x\in(a,b]</math> ו- <math>y\in[b,c)</math> . מכאן <math>|x-b|\le|x-y|<\delta\le\delta_1</math> וכן <math>|y-b|\le|x-y|<\delta\le\delta_2</math> . מכאן <math>\Big|f(x)-f(b)\Big|<\frac{\epsilon}{2}</math> וכמו כן <math>\Big|f(b)-f(y)\Big|<\frac{\epsilon}{2}</math> . כעת ניעזר באי-שוויון המשולש כדי לקבל <math>\Big|f(x)-f(y)\Big|\le\Big|f(x)-f(b)\Big|+\Big|f(b)-f(y)\Big|<\epsilon</math> |
| − | <math>|f(x)-f(b)|<\frac{\epsilon}{2}</math > וכמו כן | + | |
| − | <math>|f(b)-f(y)|<\frac{\epsilon}{2}</math>. כעת ניעזר באי שוויון המשולש כדי לקבל | + | |
| − | <math>|f(x)-f(y)|\ | + | |
===משפט=== | ===משפט=== | ||
| − | תהי f רציפה על קטע חצי אינסופי מהצורה <math>[a,\infty)</math>, כך שהגבול | + | תהי <math>f</math> רציפה על קטע חצי אינסופי מהצורה <math>[a,\infty)</math> , כך שהגבול |
| − | + | :<math>\lim_{x\to\infty}f(x)=L</math> | |
| − | + | קיים וסופי, אזי <math>f</math> רציפה במ"ש על הקטע <math>[a,\infty)</math> . | |
| − | קיים וסופי, אזי f רציפה במ"ש על הקטע <math>[a,\infty)</math>. | + | |
| − | + | ||
'''הוכחה.''' | '''הוכחה.''' | ||
| − | יהי | + | יהי <math>\epsilon>0</math> , יש למצוא <math>\delta>0</math> כך שאם המרחק בין זוג נקודות בקטע קטן מדלתא, המרחק בין התמונות שלהן תחת הפונקציה קטן מאפסילון. |
| − | לפי הנתון, קיים M כך שלכל <math>x>M</math> מתקיים <math>|f(x)-L|<\frac{\epsilon}{2}</math>. | + | לפי הנתון, קיים <math>M</math> כך שלכל <math>x>M</math> מתקיים <math>\Big|f(x)-L\Big|<\frac{\epsilon}{2}</math> . |
| − | לכן לכל <math>x_1,x_2>M</math> מתקיים <math>|f(x_1)-f(x_2)|<\epsilon</math> (בעזרת אי | + | לכן לכל <math>x_1,x_2>M</math> מתקיים <math>\Big|f(x_1)-f(x_2)\Big|<\epsilon</math> (בעזרת אי-שוויון המשולש). |
| − | כעת, לפי משפט קנטור f רציפה במ"ש בקטע <math>[a,M+1]</math>, ולכן קיים דלתא כך שלכל זוג נקודות <math>a\ | + | כעת, לפי משפט קנטור <math>f</math> רציפה במ"ש בקטע <math>[a,M+1]</math> , ולכן קיים דלתא כך שלכל זוג נקודות <math>a\le x_1,x_2\le M+1</math> הקרובות עד-כדי דלתא, מתקיים <math>\Big|f(x_1)-f(x_2)\Big|<\epsilon</math> . |
| − | אם ניקח מרחק שקטן או שווה | + | אם ניקח מרחק שקטן או שווה ל- <math>\min\{\delta,1\}</math> , יתקיים שאם <math>|x_1-x_2|<\delta</math> אזי שתי הנקודות נמצאות בקטע <math>[M,\infty)</math> או בקטע <math>[a,M+1]</math> ולכן ההפרש בין התמונות שלהן תחת <math>f</math> הוא קטן מאפסילון כפי שרצינו. |
===מסקנה - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - גבולות סופיים בקצות הקטע=== | ===מסקנה - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - גבולות סופיים בקצות הקטע=== | ||
| − | תהי f פונקציה '''רציפה על קטע''' לאו דווקא סופי, אזי אם הגבולות של הפונקציה בקצות הקטע קיימים וסופיים, הפונקציה רציפה במ"ש בקטע | + | תהי <math>f</math> פונקציה '''רציפה על קטע''' לאו דווקא סופי, אזי אם הגבולות של הפונקציה בקצות הקטע קיימים וסופיים, הפונקציה רציפה במ"ש בקטע. |
דוגמא נגדית לכיוון ההפוך - <math>f(x)=x</math> על כל ציר הממשיים. | דוגמא נגדית לכיוון ההפוך - <math>f(x)=x</math> על כל ציר הממשיים. | ||
'''שימו לב:''' יש לוודא ראשית כי הפונקציה רציפה בכל נקודה בקטע, לפני שבודקים את הגבולות בקצוות. | '''שימו לב:''' יש לוודא ראשית כי הפונקציה רציפה בכל נקודה בקטע, לפני שבודקים את הגבולות בקצוות. | ||
| − | |||
| − | |||
===משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - נגזרת חסומה=== | ===משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - נגזרת חסומה=== | ||
| שורה 155: | שורה 136: | ||
===משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - מחזורית ורציפה=== | ===משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - מחזורית ורציפה=== | ||
| − | |||
פונקציה מחזורית הרציפה על כל הממשיים, רציפה במ"ש על כל הממשיים. | פונקציה מחזורית הרציפה על כל הממשיים, רציפה במ"ש על כל הממשיים. | ||
שימו לב: פונקציה נקראת מחזורית אם קיים מספר ממשי p כך שלכל x ממשי מתקיים: | שימו לב: פונקציה נקראת מחזורית אם קיים מספר ממשי p כך שלכל x ממשי מתקיים: | ||
| − | + | :<math>f(x+p)=f(x)</math> | |
| − | + | ||
| − | + | ||
'''דוגמא.''' | '''דוגמא.''' | ||
| − | <math>f(x)=e^{-sin(x)}</math> רציפה במ"ש על כל הממשיים. | + | <math>f(x)=e^{-\sin(x)}</math> רציפה במ"ש על כל הממשיים. |
באופן דומה, כל הרכבת פונקציות רציפות, כאשר הפונקציה הכי פנימית מחזורית, רציפה במ"ש. | באופן דומה, כל הרכבת פונקציות רציפות, כאשר הפונקציה הכי פנימית מחזורית, רציפה במ"ש. | ||
| − | + | =='''אלגוריתם לבדיקת רציפות במ"ש'''== | |
| − | == '''אלגוריתם לבדיקת רציפות במ"ש''' == | + | |
| − | + | ||
[[מדיה:Uniformcontinu2013infidvir.pdf|אלגוריתם לבדיקת רציפות במ"ש]] | [[מדיה:Uniformcontinu2013infidvir.pdf|אלגוריתם לבדיקת רציפות במ"ש]] | ||
| שורה 178: | שורה 154: | ||
===1=== | ===1=== | ||
| − | *<math>f(x)= | + | *<math>f(x)=x\sin(x)</math> בקטע <math>(0,\infty)</math> |
'''פתרון.''' הפונקציה אינה רציפה במ"ש, נבנה שתי סדרות: | '''פתרון.''' הפונקציה אינה רציפה במ"ש, נבנה שתי סדרות: | ||
| − | + | :<math>x_n=\frac{1}{n}+2\pi n</math> | |
| − | + | :<math>y_n=2\pi n</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
מתקיים | מתקיים | ||
| − | + | :<math>x_n-y_n=\frac{1}{n}\to0</math> | |
| − | + | ||
| − | + | ||
אבל | אבל | ||
| − | + | :<math>f(x_n)-f(y_n)=\left(\frac{1}{n}+2\pi n\right)\sin\Big(\tfrac{1}{n}+2\pi n\Big)\to2\pi</math> | |
| − | + | ||
| − | + | ||
שכן | שכן | ||
| − | + | :<math>n\sin\left(\tfrac{1}{n}\right)=\frac{\sin\left(\tfrac{1}{n}\right)}{\frac{1}{n}}\to1</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
ולכן ההפרש בין תמונות הנקודות גדול מאשר אחד (למשל) החל משלב מסוים, לכן הפונקציה אינה רציפה במ"ש. | ולכן ההפרש בין תמונות הנקודות גדול מאשר אחד (למשל) החל משלב מסוים, לכן הפונקציה אינה רציפה במ"ש. | ||
| − | |||
| − | |||
===2=== | ===2=== | ||
| − | *<math>f(x)=ln(x)</math> בקטע <math>(1,\infty)</math> | + | *<math>f(x)=\ln(x)</math> בקטע <math>(1,\infty)</math> |
| − | נגזור את הפונקציה, לקבל <math>f'(x)=\frac{1}{x}</math> החסומה על ידי 1 בקטע, ולכן הפונקציה רציפה במ"ש בקטע. | + | נגזור את הפונקציה, לקבל <math>f'(x)=\frac{1}{x}</math> החסומה על-ידי 1 בקטע, ולכן הפונקציה רציפה במ"ש בקטע. |
===3=== | ===3=== | ||
| − | *<math>f(x)=ln(x)</math> בקטע <math>(0,\infty)</math> | + | *<math>f(x)=\ln(x)</math> בקטע <math>(0,\infty)</math> |
הפונקציה אינה חסומה על הקטע הסופי <math>(0,1)</math> ולכן לא רציפה במ"ש שם, ובוודאי אינה רציפה במ"ש בכל קטע המכיל אותו. | הפונקציה אינה חסומה על הקטע הסופי <math>(0,1)</math> ולכן לא רציפה במ"ש שם, ובוודאי אינה רציפה במ"ש בכל קטע המכיל אותו. | ||
===4=== | ===4=== | ||
| − | *<math>f(x)= | + | *<math>f(x)=x\ln(x)</math> בקטע <math>(0,\infty)</math> |
נוכיח את שלילת רציפות במ"ש: | נוכיח את שלילת רציפות במ"ש: | ||
| − | נבחר אפסילון קבוע. יהי <math>\delta >0</math> | + | נבחר אפסילון קבוע. יהי <math>\delta>0</math> |
| − | אזי ניקח <math> | + | אזי ניקח <math>x_0>1,x_1:=x_0+\frac{\delta}{2}</math> ונביט בהגדרה: |
| − | <math>|f( | + | <math>\Big|f(x_1)-f(x_0)\Big|=\Bigg|\left(x_0+\tfrac{\delta}{2}\right)\ln\left(x_0+\tfrac{\delta}{2}\right)-x_0\ln(x_0)\Bigg|=\left|\frac{\delta}{2}\ln\left(x_0+\tfrac{\delta}{2}\right)+x_0\ln\left(\frac{x_0+\tfrac{\delta}{2}}{x_0}\right)\right|</math> |
| − | מתקיים: <math>\frac{ | + | מתקיים: <math>\frac{x_0+\frac{\delta}{2}}{x_0}>1\to\ln(\frac{x_0+\frac{\delta}{2}}{x_0})>0</math> |
| − | ולכן מספיק למצוא x כך שיתקיים <math>\frac{\delta }{2}ln( | + | ולכן מספיק למצוא x כך שיתקיים <math>\frac{\delta}{2}\ln\left(x_0+\tfrac{\delta}{2}\right)\ge\epsilon</math> |
| − | ניקח <math> | + | ניקח <math>x_0>e^{\frac{2\epsilon}{\delta}}-\frac{\delta}{2}</math> וסיימנו. |
===5=== | ===5=== | ||
| − | *<math>sin\ | + | *<math>\sin\left(\tfrac{1}{x}\right)</math> בקטע <math>(0,1)</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| + | נמצא שתי סדרות שהמרחק ביניהן שואף לאפס, אבל המרחק בין הפונקציה עליהן אינו שואף לאפס. | ||
:<math>x_n=\frac{1}{\frac{\pi}{2}+2\pi n}</math> | :<math>x_n=\frac{1}{\frac{\pi}{2}+2\pi n}</math> | ||
:<math>y_n=\frac{1}{\frac{3\pi}{2}+2\pi n}</math> | :<math>y_n=\frac{1}{\frac{3\pi}{2}+2\pi n}</math> | ||
| − | |||
| − | |||
רואים כי מתקיים: | רואים כי מתקיים: | ||
| − | + | <math>|x_n-y_n|\to0</math> | |
| − | <math>|x_n-y_n|\ | + | |
וגם | וגם | ||
| − | <math>|f(x_n)-f(y_n)|=2\not\ | + | <math>\Big|f(x_n)-f(y_n)\Big|=2\not\to0</math> |
ולכן הפונקציה אינה רציפה במ"ש בקטע | ולכן הפונקציה אינה רציפה במ"ש בקטע | ||
| − | |||
===6=== | ===6=== | ||
| − | *<math> | + | *<math>x\sin\left(\tfrac{1}{x}\right)</math> בקטע <math>(0,1)</math> |
לפונקציה גבולות סופיים בשני קצוות הקטע, היא רציפה בכל נקודה בקטע ולכן רציפה שם במ"ש | לפונקציה גבולות סופיים בשני קצוות הקטע, היא רציפה בכל נקודה בקטע ולכן רציפה שם במ"ש | ||
גרסה אחרונה מ־19:03, 2 באוגוסט 2016
תוכן עניינים
- 1 רציפות במידה שווה
- 2 מבחנים לבדיקה האם פונקציה רציפה במ"ש
- 2.1 משפט - תנאי הכרחי (אך לא מספיק) לרציפות במ"ש
- 2.2 משפט - סכום רציפות במ"ש
- 2.3 משפט - תנאי שקול לאי-רציפות במ"ש - שיטת הסדרות
- 2.4 משפט - תנאי הכרחי (אבל לא מספיק) לרציפות במ"ש - חסימות על קטע סופי
- 2.5 משפט קנטור
- 2.6 משפט - הרכבת פונקציות רציפות במ"ש
- 2.7 משפט - חלוקה לתתי-קטעים
- 2.8 משפט
- 2.9 מסקנה - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - גבולות סופיים בקצות הקטע
- 2.10 משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - נגזרת חסומה
- 2.11 משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - מחזורית ורציפה
- 3 אלגוריתם לבדיקת רציפות במ"ש
- 4 תרגילים
רציפות במידה שווה
עד כה הגדרנו רציפות באופן נקודתי ואמרנו שפונקציה רציפה בקטע אם היא רציפה בכל נקודה בקטע בנפרד.
באופן אינטואיטיבי, אומרים כי פונקציה מתכנסת 'יותר מהר' אל הגבול שלה, אם הדלתא הנדרש לאפסילון הוא גדול יותר (כלומר הפונקציה קרובה לגבול בתחום יותר רחב). אנו רוצים להגדיר פונקציות אשר מהירות ההתכנסות שלהן דומה בכל נקודה בקטע מסוים.
הגדרה.
פונקציה  נקראת רציפה במידה שווה (רציפה במ"ש) בקטע A אם:
נקראת רציפה במידה שווה (רציפה במ"ש) בקטע A אם:
- לכל
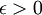 קיים
קיים 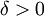 כך שלכל זוג נקודות
כך שלכל זוג נקודות 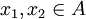 המקיימות
המקיימות 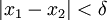 מתקיים
מתקיים 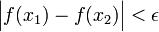 .
.
שימו לב כי ברציפות רגילה בקטע A, לכל נקודה בקטע ההתאמה של הדלתא לאפסילון עשויה להיות שונה. כאשר הפונקציה רציפה במ"ש, לכל אפסילון יש דלתא המתאים לכל הקטע A.
הערה: ברור שאם פונקציה רציפה במ"ש על קטע A, היא גם רציפה במ"ש על כל קטע המוכל ב-A.
דוגמאות.
נבחן את הפונקציה 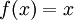 , ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים.
, ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים.
אכן, לכל אפסילון ניקח דלתא שווה לאפסילון ונקבל כי 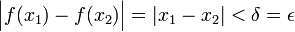
בדוגמא הבאה נלמד כי פונקציה מסוימת עשוייה להיות רציפה במ"ש בקטע מסוים אך לא רציפה במ"ש בקטע אחר. כפי שנראה בהמשך, כל פונקציה הרציפה על קטע סופי וסגור רציפה בו במ"ש, ואילו ישנן פונקציות רציפות שאינן רציפות במ"ש על כל ציר הממשיים.
ראשית, נביט ב 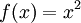 על הקטע הסופי
על הקטע הסופי 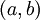 . יהי
. יהי 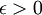 , אזי:
, אזי:
כעת, אם ניקח 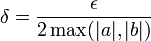 נקבל את הדרוש.
נקבל את הדרוש.
עכשיו, נבחן את אותה הפונקציה 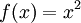 על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש.
על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש.
ניקח 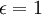 . צריך להוכיח כי לכל
. צריך להוכיח כי לכל 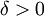 קיים זוג מספרים ממשיים המקיימים
קיים זוג מספרים ממשיים המקיימים 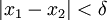 וגם
וגם 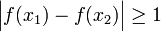 .
.
ניקח 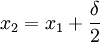 ונראה כי אם נבחר את
ונראה כי אם נבחר את 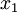 להיות גדול מספיק, נקבל את הדרוש. ברור כי
להיות גדול מספיק, נקבל את הדרוש. ברור כי 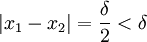
ברור שאם נגדיל את 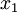 מספיק נקבל את הדרוש.
מספיק נקבל את הדרוש.
מבחנים לבדיקה האם פונקציה רציפה במ"ש
משפט - תנאי הכרחי (אך לא מספיק) לרציפות במ"ש
פונקציה הרציפה במ"ש על קטע רציפה שם, דהיינו אם הפונקציה לא רציפה או לא מוגדרת בנקודה אחת בקטע (לפחות) היא אינה רציפה שם במ"ש.
משפט - סכום רציפות במ"ש
סכום וכפל בקבוע של רציפות במ"ש - רציף במ"ש.
שימו לב, כפל אינו רציף במ"ש בהכרח, לדוגמא 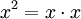 , כאשר הפונקציה משמאל אינה רציפה במ"ש על כל הממשיים, ואילו הפונקציות מימין כן.
, כאשר הפונקציה משמאל אינה רציפה במ"ש על כל הממשיים, ואילו הפונקציות מימין כן.
משפט - תנאי שקול לאי-רציפות במ"ש - שיטת הסדרות
פונקציה f אינה רציפה במ"ש בקטע A אם"ם קיים זוג סדרות (עם אברים מ-A) המקיימות:
וגם
הוכחה.
אם הפונקציה אינה רציפה במ"ש אזי קיים 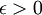 כך שלכל
כך שלכל 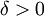 יש זוג מספרים בקטע במרחק קטן מדלתא, כך שהפרש התמונות ביניהם גדול או שווה לאפסילון.
יש זוג מספרים בקטע במרחק קטן מדלתא, כך שהפרש התמונות ביניהם גדול או שווה לאפסילון.
ניקח סדרת דלתאות כלשהי השואפת לאפס. הסדרות המורכבות מהזוגות המותאמים לדלתאות מקיימות את הדרוש.
בכיוון ההפוך, אם יש זוג סדרות כזה, כיון שסדרת ההפרשים בין התמונות אינה שואפת לאפס יש לה תת-סדרה שמתכנסת למספר שונה מאפס (הגבול העליון). תת הסדרות המתאימות של הזוגות יספקו זוג מתאים לכל דלתא, כאשר האפסילון יהיה חצי מגבול סדרת ההפרשים.
משפט - תנאי הכרחי (אבל לא מספיק) לרציפות במ"ש - חסימות על קטע סופי
פונקציה רציפה במ"ש על קטע סופי חסומה שם
דוגמא נגדית לכיוון ההפוך - 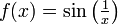 חסומה אך אינה רציפה במ"ש בקטע
חסומה אך אינה רציפה במ"ש בקטע 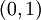
משפט קנטור
פונקציה רציפה על קטע סגור וסופי רציפה שם במ"ש
משפט - הרכבת פונקציות רציפות במ"ש
נניח  רציפה במ"ש על קטע המכיל את התמונה של פונקציה רציפה במ"ש
רציפה במ"ש על קטע המכיל את התמונה של פונקציה רציפה במ"ש  . אזי ההרכבה
. אזי ההרכבה 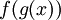 רציפה במ"ש
רציפה במ"ש
משפט - חלוקה לתתי-קטעים
אם  רציפה במ"ש על הקטעים
רציפה במ"ש על הקטעים ![(a,b],[b,c)](/images/math/7/d/9/7d9d995700caea90ad4bcc21bba0900c.png) (לאו דווקא קצות סופיים), אזי היא רציפה במ"ש באיחוד
(לאו דווקא קצות סופיים), אזי היא רציפה במ"ש באיחוד 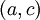
הוכחה.
יהי 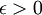 .
.
 רציפה במ"ש ב-
רציפה במ"ש ב- ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ולכן קיים
ולכן קיים 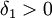 כך שלכל
כך שלכל ![x,y\in(a,b]](/images/math/7/e/e/7ee5d2274c73502ed632a221c40d6c97.png) המקיימים
המקיימים 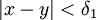 מתקיים
מתקיים 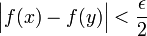 .
.
 רציפה במ"ש ב-
רציפה במ"ש ב- 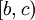 ולכן קיים
ולכן קיים 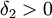 כך שלכל
כך שלכל 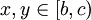 המקיימים
המקיימים 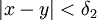 מתקיים
מתקיים 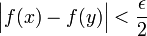 .
.
יהי 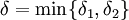 . אזי
. אזי 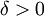 . נראה שלכל
. נראה שלכל 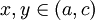 המקיימים
המקיימים 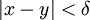 מתקיים
מתקיים 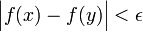 .
.
נניח 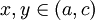 כך ש-
כך ש- 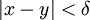 . יתכנו שלושה מצבים:
. יתכנו שלושה מצבים:
א) ![x,y\in(a,b]](/images/math/7/e/e/7ee5d2274c73502ed632a221c40d6c97.png) . אזי
. אזי 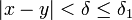 ומכאן
ומכאן 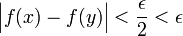 .
.
ב) 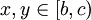 ומכיון ש-
ומכיון ש- 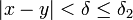 נסיק ש-
נסיק ש- 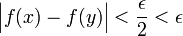 .
.
ג) אחת מהנקודות ב- ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) והשניה ב-
והשניה ב- 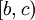 . נניח בה"כ ש-
. נניח בה"כ ש- ![x\in(a,b]](/images/math/4/3/f/43f86f76ef527b770063737b76a452a7.png) ו-
ו- 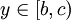 . מכאן
. מכאן 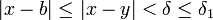 וכן
וכן 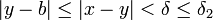 . מכאן
. מכאן 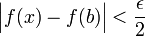 וכמו כן
וכמו כן 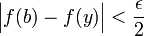 . כעת ניעזר באי-שוויון המשולש כדי לקבל
. כעת ניעזר באי-שוויון המשולש כדי לקבל 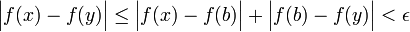
משפט
תהי  רציפה על קטע חצי אינסופי מהצורה
רציפה על קטע חצי אינסופי מהצורה 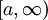 , כך שהגבול
, כך שהגבול
קיים וסופי, אזי  רציפה במ"ש על הקטע
רציפה במ"ש על הקטע 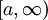 .
.
הוכחה.
יהי 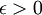 , יש למצוא
, יש למצוא 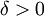 כך שאם המרחק בין זוג נקודות בקטע קטן מדלתא, המרחק בין התמונות שלהן תחת הפונקציה קטן מאפסילון.
כך שאם המרחק בין זוג נקודות בקטע קטן מדלתא, המרחק בין התמונות שלהן תחת הפונקציה קטן מאפסילון.
לפי הנתון, קיים 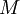 כך שלכל
כך שלכל 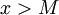 מתקיים
מתקיים 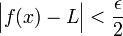 .
.
לכן לכל 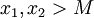 מתקיים
מתקיים 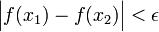 (בעזרת אי-שוויון המשולש).
(בעזרת אי-שוויון המשולש).
כעת, לפי משפט קנטור  רציפה במ"ש בקטע
רציפה במ"ש בקטע ![[a,M+1]](/images/math/7/9/6/7966a66d9d351fc2d8c180e5fa9d5c50.png) , ולכן קיים דלתא כך שלכל זוג נקודות
, ולכן קיים דלתא כך שלכל זוג נקודות 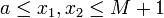 הקרובות עד-כדי דלתא, מתקיים
הקרובות עד-כדי דלתא, מתקיים 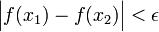 .
.
אם ניקח מרחק שקטן או שווה ל- 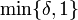 , יתקיים שאם
, יתקיים שאם 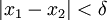 אזי שתי הנקודות נמצאות בקטע
אזי שתי הנקודות נמצאות בקטע 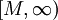 או בקטע
או בקטע ![[a,M+1]](/images/math/7/9/6/7966a66d9d351fc2d8c180e5fa9d5c50.png) ולכן ההפרש בין התמונות שלהן תחת
ולכן ההפרש בין התמונות שלהן תחת  הוא קטן מאפסילון כפי שרצינו.
הוא קטן מאפסילון כפי שרצינו.
מסקנה - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - גבולות סופיים בקצות הקטע
תהי  פונקציה רציפה על קטע לאו דווקא סופי, אזי אם הגבולות של הפונקציה בקצות הקטע קיימים וסופיים, הפונקציה רציפה במ"ש בקטע.
פונקציה רציפה על קטע לאו דווקא סופי, אזי אם הגבולות של הפונקציה בקצות הקטע קיימים וסופיים, הפונקציה רציפה במ"ש בקטע.
דוגמא נגדית לכיוון ההפוך - 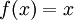 על כל ציר הממשיים.
על כל ציר הממשיים.
שימו לב: יש לוודא ראשית כי הפונקציה רציפה בכל נקודה בקטע, לפני שבודקים את הגבולות בקצוות.
משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - נגזרת חסומה
פונקציה גזירה שנגזרתה חסומה בקטע, רציפה שם במ"ש.
דוגמא נגדית לכיוון ההפוך - 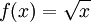 בקטע הפתוח
בקטע הפתוח 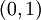
משפט - תנאי מספיק (אבל לא הכרחי) לרציפות במ"ש - מחזורית ורציפה
פונקציה מחזורית הרציפה על כל הממשיים, רציפה במ"ש על כל הממשיים.
שימו לב: פונקציה נקראת מחזורית אם קיים מספר ממשי p כך שלכל x ממשי מתקיים:
דוגמא.
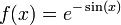 רציפה במ"ש על כל הממשיים.
רציפה במ"ש על כל הממשיים.
באופן דומה, כל הרכבת פונקציות רציפות, כאשר הפונקציה הכי פנימית מחזורית, רציפה במ"ש.
אלגוריתם לבדיקת רציפות במ"ש
תרגילים
בדוק רציפות במ"ש של הפונקציות הבאות בקטעים הנתונים:
1
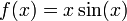 בקטע
בקטע 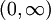
פתרון. הפונקציה אינה רציפה במ"ש, נבנה שתי סדרות:
מתקיים
אבל
שכן
ולכן ההפרש בין תמונות הנקודות גדול מאשר אחד (למשל) החל משלב מסוים, לכן הפונקציה אינה רציפה במ"ש.
2
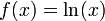 בקטע
בקטע 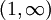
נגזור את הפונקציה, לקבל 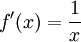 החסומה על-ידי 1 בקטע, ולכן הפונקציה רציפה במ"ש בקטע.
החסומה על-ידי 1 בקטע, ולכן הפונקציה רציפה במ"ש בקטע.
3
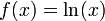 בקטע
בקטע 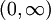
הפונקציה אינה חסומה על הקטע הסופי 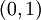 ולכן לא רציפה במ"ש שם, ובוודאי אינה רציפה במ"ש בכל קטע המכיל אותו.
ולכן לא רציפה במ"ש שם, ובוודאי אינה רציפה במ"ש בכל קטע המכיל אותו.
4
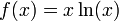 בקטע
בקטע 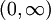
נוכיח את שלילת רציפות במ"ש:
נבחר אפסילון קבוע. יהי 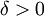
אזי ניקח 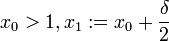 ונביט בהגדרה:
ונביט בהגדרה:
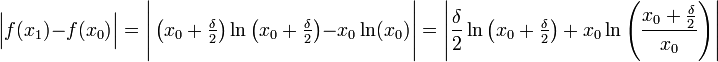
מתקיים: 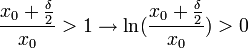
ולכן מספיק למצוא x כך שיתקיים 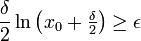
ניקח 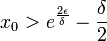 וסיימנו.
וסיימנו.
5
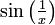 בקטע
בקטע 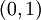
נמצא שתי סדרות שהמרחק ביניהן שואף לאפס, אבל המרחק בין הפונקציה עליהן אינו שואף לאפס.
רואים כי מתקיים:
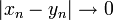
וגם
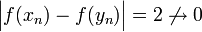
ולכן הפונקציה אינה רציפה במ"ש בקטע
6
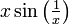 בקטע
בקטע 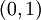
לפונקציה גבולות סופיים בשני קצוות הקטע, היא רציפה בכל נקודה בקטע ולכן רציפה שם במ"ש