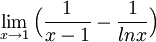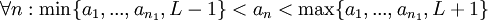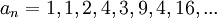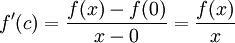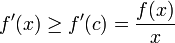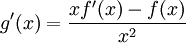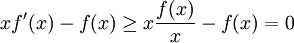הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/פתרון מועד א מדמח"
מתוך Math-Wiki
(←שאלה 2) |
(←שאלה 3) |
||
| שורה 48: | שורה 48: | ||
==שאלה 3== | ==שאלה 3== | ||
| + | קבעו האם קיים הגבול ואם כן מצאו אותו: | ||
| + | |||
| + | |||
| + | א. <math>\lim_{n\rightarrow\infty}\sqrt[n]{1^n+2^n+...+2012^n}</math> | ||
| + | |||
| + | |||
| + | ב. <math>\lim_{n\rightarrow\infty}a_n</math>, כאשר <math>a_1=1</math>, ו- <math>a_{n+1}=sin(a_n)</math> | ||
| + | |||
| + | |||
| + | ג. <math>\lim_{x\rightarrow\infty}(sin\sqrt{x-a}-sin\sqrt{x})</math> | ||
| + | |||
| + | |||
| + | ד. <math>\lim_{x\rightarrow 1}\Big(\frac{1}{x-1}-\frac{1}{lnx}\Big)</math> | ||
| + | |||
| + | |||
| + | ===פתרון=== | ||
גרסה מ־18:09, 8 בפברואר 2012
שאלה 1
א. הוכח כי כל סדרה מתכנסת חסומה
ב. הוכח/הפרך: אם ![\lim\sqrt[n]{a_n}=L](/images/math/f/2/8/f28a854d1a5289cb61e520b8c750a947.png) אזי
אזי 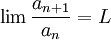
פתרון
א. כיוון שהסדרה מתכנסת, קיים מקום בסדרה 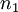 כך שלכל
כך שלכל 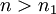 מתקיים
מתקיים 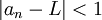 ולכן
ולכן 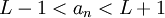 . סה"כ:
. סה"כ:
ב. הפרכה: ניקח סדרה אשר במקומות הזוגיים שלה שווה  , ובמקומות האי-זוגיים
, ובמקומות האי-זוגיים 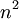 :
:
קל לראות כי ![\lim\sqrt[n]{a_n}=1](/images/math/6/9/3/693017a7c48e190580e5110d552071ed.png) , אבל לא קיים הגבול
, אבל לא קיים הגבול 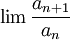
שאלה 2
נניח כי f פונקציה רציפה ב- 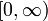 , גזירה ב-
, גזירה ב- 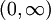 . בנוסף נתון כי
. בנוסף נתון כי 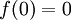 והנגזרת
והנגזרת 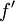 מונוטונית עולה ב-
מונוטונית עולה ב- 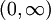 .
.
א. הוכיחו כי 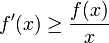 ב-
ב- 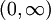 .
.
ב. הוכיחו כי הפונקציה 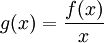 מונוטונית עולה ב-
מונוטונית עולה ב- 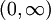 .
.
פתרון
א. יהי 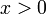 . נפעיל את משפט לגראנג' על הפונקציה f בקטע
. נפעיל את משפט לגראנג' על הפונקציה f בקטע ![[0,x]](/images/math/4/7/e/47e2767cb741a37b889f1968c34f8398.png) . לכן קיימת נקודה
. לכן קיימת נקודה 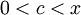 כך ש:
כך ש:
אבל מתוך מונוטוניות הנגזרת, אנו מקבלים:
כפי שרצינו.
ב. נוכיח כי הנגזרת חיובית ולכן הפונקציה מונוטונית עולה
כיוון שהמכנה חיובי תמיד, סימן הנגזרת נקבע על ידי המונה. אבל לפי סעיף א':
שאלה 3
קבעו האם קיים הגבול ואם כן מצאו אותו:
א. ![\lim_{n\rightarrow\infty}\sqrt[n]{1^n+2^n+...+2012^n}](/images/math/8/d/a/8dac8b93073ff5b04298d225958ab37e.png)
ב. 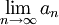 , כאשר
, כאשר 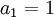 , ו-
, ו- 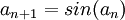
ג. 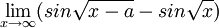
ד.