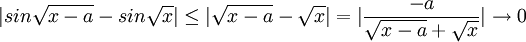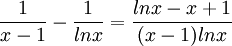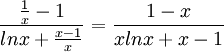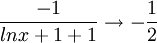הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/פתרון מועד א מדמח"
(←שאלה 3) |
(←פתרון) |
||
| שורה 64: | שורה 64: | ||
===פתרון=== | ===פתרון=== | ||
| + | |||
| + | א. | ||
| + | |||
| + | נפעיל את משפט הסנדביץ': | ||
| + | |||
| + | |||
| + | ::<math>2012=\sqrt[n]{2012^n}\leq \sqrt[n]{1^n+2^n+...+2012^n}\leq \sqrt[n]{2012^n+2012^n+...+2012^n}=\sqrt[n]{2012\cdot 2012^n}\rightarrow 2012</math> | ||
| + | |||
| + | |||
| + | ב. | ||
| + | |||
| + | ידוע כי עבור ערכים חיוביים <math>sin(x)<x</math> ולכן קל להוכיח באינדוקציה כי זו סדרה מונוטונית יורדת וחסומה מלרע על ידי אפס, ולכן מתכנס. | ||
| + | |||
| + | <math>L=sin(L)</math> ולכן <math>L=0</math>. | ||
| + | |||
| + | אכן, אם היה פתרון אחר למשוואה <math>x-sin(x)=0</math> הקטן מאחד, אזי הנגזרת הייתה צריכה להתאפס בין אפס לאחד (לפי רול) וקל לוודא כי זה לא קורה. | ||
| + | |||
| + | |||
| + | ג. | ||
| + | |||
| + | כפי שראינו בכיתה, ניתן להוכיח בעזרת לגראנג' כי <math>|sin(x)-sin(y)|\leq |x-y|</math> לכן, | ||
| + | |||
| + | ::<math>|sin\sqrt{x-a}-sin\sqrt{x}|\leq |\sqrt{x-a}-\sqrt{x}|=|\frac{-a}{\sqrt{x-a}+\sqrt{x}}|\rightarrow 0</math> | ||
| + | |||
| + | |||
| + | ד. | ||
| + | |||
| + | ::<math>\frac{1}{x-1}-\frac{1}{lnx}=\frac{lnx-x+1}{(x-1)lnx}</math> | ||
| + | |||
| + | נגזור את המונה ואת המכנה לקבל: | ||
| + | |||
| + | ::<math>\frac{\frac{1}{x}-1}{lnx+\frac{x-1}{x}}=\frac{1-x}{xlnx+x-1}</math> | ||
| + | |||
| + | שוב נגזור את המונה ואת המכנה לקבל: | ||
| + | |||
| + | ::<math>\frac{-1}{lnx + 1 +1}\rightarrow -\frac{1}{2}</math> | ||
| + | |||
| + | |||
| + | ולכן לפי כלל לופיטל, זה גם הגבול המקורי. | ||
גרסה מ־18:26, 8 בפברואר 2012
שאלה 1
א. הוכח כי כל סדרה מתכנסת חסומה
ב. הוכח/הפרך: אם ![\lim\sqrt[n]{a_n}=L](/images/math/f/2/8/f28a854d1a5289cb61e520b8c750a947.png) אזי
אזי 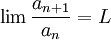
פתרון
א. כיוון שהסדרה מתכנסת, קיים מקום בסדרה 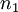 כך שלכל
כך שלכל 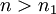 מתקיים
מתקיים 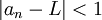 ולכן
ולכן 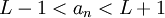 . סה"כ:
. סה"כ:
ב. הפרכה: ניקח סדרה אשר במקומות הזוגיים שלה שווה  , ובמקומות האי-זוגיים
, ובמקומות האי-זוגיים 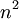 :
:
קל לראות כי ![\lim\sqrt[n]{a_n}=1](/images/math/6/9/3/693017a7c48e190580e5110d552071ed.png) , אבל לא קיים הגבול
, אבל לא קיים הגבול 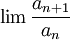
שאלה 2
נניח כי f פונקציה רציפה ב- 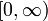 , גזירה ב-
, גזירה ב- 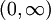 . בנוסף נתון כי
. בנוסף נתון כי 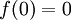 והנגזרת
והנגזרת 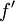 מונוטונית עולה ב-
מונוטונית עולה ב- 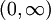 .
.
א. הוכיחו כי 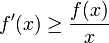 ב-
ב- 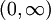 .
.
ב. הוכיחו כי הפונקציה 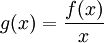 מונוטונית עולה ב-
מונוטונית עולה ב- 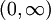 .
.
פתרון
א. יהי 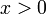 . נפעיל את משפט לגראנג' על הפונקציה f בקטע
. נפעיל את משפט לגראנג' על הפונקציה f בקטע ![[0,x]](/images/math/4/7/e/47e2767cb741a37b889f1968c34f8398.png) . לכן קיימת נקודה
. לכן קיימת נקודה 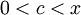 כך ש:
כך ש:
אבל מתוך מונוטוניות הנגזרת, אנו מקבלים:
כפי שרצינו.
ב. נוכיח כי הנגזרת חיובית ולכן הפונקציה מונוטונית עולה
כיוון שהמכנה חיובי תמיד, סימן הנגזרת נקבע על ידי המונה. אבל לפי סעיף א':
שאלה 3
קבעו האם קיים הגבול ואם כן מצאו אותו:
א. ![\lim_{n\rightarrow\infty}\sqrt[n]{1^n+2^n+...+2012^n}](/images/math/8/d/a/8dac8b93073ff5b04298d225958ab37e.png)
ב. 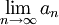 , כאשר
, כאשר 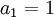 , ו-
, ו- 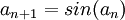
ג. 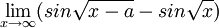
ד. 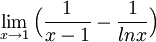
פתרון
א.
נפעיל את משפט הסנדביץ':
ב.
ידוע כי עבור ערכים חיוביים 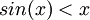 ולכן קל להוכיח באינדוקציה כי זו סדרה מונוטונית יורדת וחסומה מלרע על ידי אפס, ולכן מתכנס.
ולכן קל להוכיח באינדוקציה כי זו סדרה מונוטונית יורדת וחסומה מלרע על ידי אפס, ולכן מתכנס.
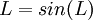 ולכן
ולכן 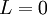 .
.
אכן, אם היה פתרון אחר למשוואה 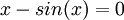 הקטן מאחד, אזי הנגזרת הייתה צריכה להתאפס בין אפס לאחד (לפי רול) וקל לוודא כי זה לא קורה.
הקטן מאחד, אזי הנגזרת הייתה צריכה להתאפס בין אפס לאחד (לפי רול) וקל לוודא כי זה לא קורה.
ג.
כפי שראינו בכיתה, ניתן להוכיח בעזרת לגראנג' כי 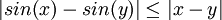 לכן,
לכן,
ד.
נגזור את המונה ואת המכנה לקבל:
שוב נגזור את המונה ואת המכנה לקבל:
ולכן לפי כלל לופיטל, זה גם הגבול המקורי.
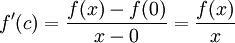
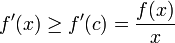
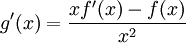
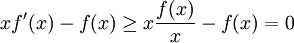
![2012=\sqrt[n]{2012^n}\leq \sqrt[n]{1^n+2^n+...+2012^n}\leq \sqrt[n]{2012^n+2012^n+...+2012^n}=\sqrt[n]{2012\cdot 2012^n}\rightarrow 2012](/images/math/1/7/f/17f5ea3e605701d5a12b02f9fed5eddb.png)