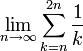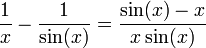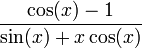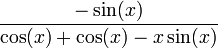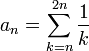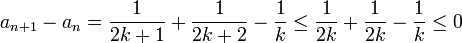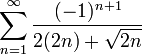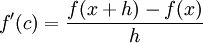88-132 אינפי 1 סמסטר א' תשעב/פתרון מועד א מתמטיקאים
תוכן עניינים
שאלה 1
צטטו והוכיחו את הלמה של קנטור
שאלה 2
א. חשבו את הגבול
ב. קבעו האם הגבול קיים:
פתרון
א.
כיון שהמונה והמכנה שואפים ל-0, ניתן להפעיל את כלל לופיטל. אם הגבול קיים לאחר גזירת המונה והמכנה בנפרד אז הוא שווה לגבול המקורי וסיימנו.
שוב, המונה והמכנה שואפים לאפס ולכן ניתן להפעיל את כלל לופיטל.
כעת המונה שואף לאפס ואילו המכנה שואף לשתיים ולכן סה"כ הגבול הוא 0.
ב. נסמן את אברי הסדרה
קל לראות כי
ולכן הסדרה מונוטונית יורדת וחסומה מלרע על-ידי  ולכן מתכנסת.
ולכן מתכנסת.
שאלה 3
קבעו לגבי כל טור האם הוא מתכנס בהחלט/בתנאי/מתבדר:
א. 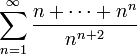
ב. 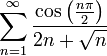
פתרון
א. 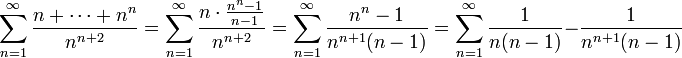
ואלה שני טורים מתכנסים ולכן סה"כ הטור מתכנס בהחלט.
ב.כיון שהקוסינוס מקבל את הערכים 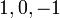 במחזוריות הידועה, טור זה בעצם שווה לטור
במחזוריות הידועה, טור זה בעצם שווה לטור
קל לראות שזהו טור שאינו מתכנס בהחלט כיון שהוא חבר של הטור ההרמוני, אבל כן מתכנס בתנאי לפי משפט לייבניץ.
שאלה 4
תהי  מוגדרת על כל הממשיים, רציפה ב-
מוגדרת על כל הממשיים, רציפה ב-  ומקיימת
ומקיימת 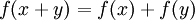 לכל זוג מספרים
לכל זוג מספרים 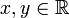 .
.
הוכיחו כי  רציפה על כל הממשיים.
רציפה על כל הממשיים.
פתרון
- ראשית נבחין כי
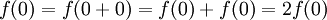 ולכן
ולכן 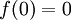
- כעת, נחשב את גבול הפונקציה בנקודה כללית לפי היינה:
- תהי
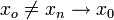 , אזי
, אזי 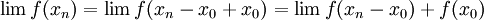
- כיון שהפונקציה רציפה ב-
 וכיון ש-
וכיון ש- 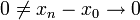 , מתקיים
, מתקיים 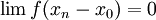
- ביחד
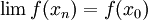 , ולכן לפי היינה מתקיים
, ולכן לפי היינה מתקיים 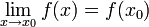 ולכן הפונקציה רציפה.
ולכן הפונקציה רציפה.
שאלה 5
מצאו פולינום 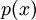 כך שלכל
כך שלכל ![x\in [0,1]](/images/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) מתקיים
מתקיים 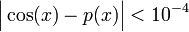
פתרון
קלי קלות באמצעות טיילור.
מי מתנדב לתרום את התשובה המלאה?
אני!
לפי [פונקציה זו] ניתן לראות שבסה"כ צריך לגזור כמה פעמים (אם כי זה היה טריקי ונאלצתי לכתת חיפושיי באינטרנט). ע"פ פיתוח טיילור הפולינום של קוסינוס זה מה שמופיע וזה מספיק בשביל לקיים את התנאי הדרוש.
אני צודק ארז או שזה לא מספיק?\\
אז ככה: ניקח את 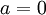 ואז כל סינוס מתאפס ובעצם מה שנשאר זה הנוסחה הבאה:
ואז כל סינוס מתאפס ובעצם מה שנשאר זה הנוסחה הבאה:
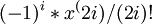 כי קוסינוס אפס תמיד שווה אחד, ואז מה שקובע זה מספר הגזירה לסימן.עכשיו רק נותר למצוא את ה-I שיביא את השארית הרצויה, והוא שלוש(שימו לב שהתחלתי מאפס)
כי קוסינוס אפס תמיד שווה אחד, ואז מה שקובע זה מספר הגזירה לסימן.עכשיו רק נותר למצוא את ה-I שיביא את השארית הרצויה, והוא שלוש(שימו לב שהתחלתי מאפס)
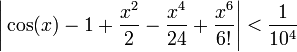
שאלה 6
תהי  פונקציה מוגדרת וגזירה על כל הממשיים, ונניח כי קיים הגבול
פונקציה מוגדרת וגזירה על כל הממשיים, ונניח כי קיים הגבול 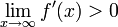 .
.
הוכיחו כי  אינה חסומה מלעיל.
אינה חסומה מלעיל.
פתרון
- נסמן
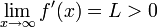 . לכן קיים
. לכן קיים 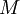 כך שלכל
כך שלכל 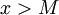 מתקיים
מתקיים 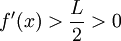 .
. - לכן, החל מ-
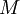 הנגזרת חיובית ממש ולכן הפונקציה מונוטונית עולה.
הנגזרת חיובית ממש ולכן הפונקציה מונוטונית עולה. - נניח בשלילה כי הפונקציה
 חסומה, לכן היא מונוטונית וחסומה ולכן מתכנסת למספר ממשי אשר נסמנו
חסומה, לכן היא מונוטונית וחסומה ולכן מתכנסת למספר ממשי אשר נסמנו  .
. - לפי הגדרת הגבול, קיים
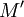 כך שלכל
כך שלכל 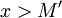 מתקיים
מתקיים 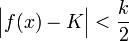 .
. - לכן ביחד לכל זוג
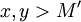 מתקיים
מתקיים 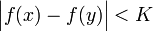
- ניקח
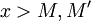 אזי לכל
אזי לכל 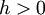 לפי משפט לגראנז' קיים
לפי משפט לגראנז' קיים 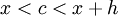 עבורו
עבורו
- כעת, מתקיים
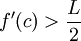 , אבל מצד שני
, אבל מצד שני 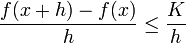 ולכן עבור
ולכן עבור 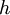 גדול מספיק נקבל סתירה.
גדול מספיק נקבל סתירה.
![\lim_{x\to0}\left[\frac1x-\frac{1}{\sin(x)}\right]](/images/math/4/1/1/41164a207d88000d24fd978d9c7e5d95.png)